Ch5. Machine Learning Basics

TIMESTAMP
@200920 시작
@200924 시작

들어가기 전에

• 머신러닝 중 하나인 딥러닝을 잘 이해하기 위해서는 머신러닝의 기본 원리를 확실히 이해해야 한다.
  • 이 장에서는 이 책의 나머지에 적용될 가장 중요한 일반적인 원칙을 간단히 다룬다.
  • 딥러닝 알고리즘의 개발에 크게 영향을 준 전통적인 머신러닝 기술에 대한 몇 가지 측면을 다룬다.
• 학습 알고리즘이 무엇인지에 대한 정의로 시작하고 예시(선형회귀)를 제시한다. 그 다음 학습 데이터를 fitting하는 문제가 새로운 데이터로 일반화되는 패턴을 찾는 문제와 어떻게 다른지 설명한다.
• 대부분의 머신러닝 알고리즘은 학습 알고리즘 외에 결정되어야 하는 하이퍼파라미터라는 세팅이 있고, 추가적인 데이터를 사용하여 어떻게 설정할지 설명한다.
• 머신러닝은 본질적으로 복잡한 함수를 통계적으로 추정하기 위해 컴퓨터를 사용하는 것에 중점을 두고, 반면 이러한 함수에 대한 신뢰구간을 입증하는 데는 중점을 두지 않는 응용 통계의 한 형태이다.
  • 그러므로 통계에 대한 두 가지 중심적인 접근(빈도주의와 베이지안 추론)을 제시한다.
• 대부분의 머신러닝 알고리즘은 지도 학습과 비지도 학습으로 나눌 수 있다.
• 대부분의 딥러닝 알고리즘은 stochastic gradient descent이라는 최적화 알고리즘을 기반으로 한다.
  • 최적화 알고리즘, 비용함수, 모델 및 데이터와 같은 다양한 알고리즘 구성 요소를 결합하여 머신러닝 알고리즘을 구축하는 방법을 설명한다.
• 마지막으로 섹션 5.11에서는 일반화하는데 제약이 있는 기존의 머신러닝의 몇 가지를 설명한다. 이러한 장애물을 극복하기 위해 딥러닝 알고리즘이 발전되어 왔다.

Learning Algorithms

• 머신러닝은 데이터에서 학습할 수 있는 알고리즘이다.

  학습이란 무엇인가? (Mitchell, 1997)
  A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E."

The Task, T

example, features

The Performance Measure, P

accuracy, error rate

The Experience, E

unsupervised, supervised
dataset, data points
Unsupervised learning algorithms
Supervised learning algorithms : label, target
reinforcement learning
design matrix

Example: Linear Regression

linear regression
parameters
weights
test set
mean squared error
normal equations
bias

Capacity, Overfitting, Underfitting

Generalization error

• 머신러닝의 핵심 과제는 모델이 학습된 데이터뿐 아니라 이전에는 보지 못했던 입력에 대해서도 잘 수행해야한다는 것이고 이를 일반화(generalization)라고 한다.
• 일반적으로 머신러닝 모델 학습을 할 때, 학습 데이터에 액세스할 수 있고, training error를 계산할 수 있으며 이를 줄일 수 있다. 지금까지는 단순히 최적화의 문제로, 이와 구별되는 머신러닝은 generalization error 혹은 test error라고도 불리는 오류 또한 낮추고자 한다는 것이다.
  • Generalization error는 새로운 입력에서 기대되는 오류로 정의되며, 실제로 접하게 될 것으로 예상되는 입력의 분포에서 도출된 다양한 경우의 입력의 기대값을 취해 구한다.
• 일반적으로 학습 데이터와 분리되어 수집된 테스트셋(test set)머신러닝 모델의 generalization error를 추정한다.
• 선형회귀 예제에서, training error을 최소화시켜 모델을 학습시킨다.
  $\frac{1}{m^{(train)}}||\bm{X}^{(train)}\bm{w}-\bm{y}^{(train)}||^2_2$
  하지만 실제로는 중요하게 생각하는 것은 test error, $\frac{1}{m^{(test)}}||\bm{X}^{(test)}\bm{w}-\bm{y}^{(test)}||^2_2$ 이다.

Statistical learing theory

• 학습 데이터만 관찰할 때 테스트셋의 성능에 어떻게 영향을 미칠 수 있을까? Statistical learning theory가 이에 대한 몇 가지 해답을 제시한다.
  • 만약 학습과 테스트가 임의로 수집하면 우리가 할 수 있는 것은 없다.
  • 만약 수집하는 방법에 대해 몇 가지 가정을 할 수 있다면 그 이상을 할 수 있다.
• 학습 및 테스트셋은 data generating process이라고 하는 데이터의 확률 분포에 의해 생성된다.
• 일반적으로 우리는 i.i.d. assumption 가정을 한다.
  • 각 데이터셋의 샘플들은 서로 독립적(independent)이다.
  • 학습셋과 테스트셋은 같은 확률 분포에서 추출되어 동일하게 분포한다(identically distributed).
• 이 가정을 통하여 단일 샘플에 대한 확률분포로 data generating process을 설명할 수 있다. 그런 다음 동일한 분포를 사용하여 모든 학습 샘플과 테스트 샘플을 생성하는 데 사용할 수 있다. 이렇게 공유되는 기본적인 분포를 data generating distribution이라고 하며, $p_{data}$라고 한다.
• 이러한 확률적인 프레임워크와 i.i.d 가정은 training error와 test error간의 관계를 수학적으로 연구할 수 있게 한다.

generalization
training error, generalization error, test error
test set
statistical learning theory
data generating process : i.i.d. assumption
inependent, identically distributed, data generating distribution
underfitting, overfitting
capacity
hypothesis space
representational capacity, effective capacity
Occam's razor
Vapnik-Chervonenkis dimension
non-parametric
nearest neighbor regression
Bayes error

The No Free Lunch Theorem

no free lunch theorem

Regularization

weight decay
regularizer
regularization

Hyperparameters and Validation Sets

hyperparameters
capacity
validation set

Cross-Validation

Estimators, Bias and Variance

Point Estimation

point estimator, statistic
Function Estimation

Bias

unbiased
asymptotically unbiased
Example: Bernoulli Distribution
Example: Gaussian Distribution Estimator of the Mean : sample mean,
Example: Estimaros of the Variance of a Gaussian Distribution : sample variance, unbiased sample variance

Variance and Standard Error

variance, standard error
Example: Bernoulli Distribution

Trading off Bias and Variance to Minimize Mean Squared Error

mean squared error

Consistency

consistency
Almost sure, Almost sure convergence

Maximum Likelihood Estimation

Conditional Log-Likelihood and Mean Squared Error

Example: Linear Regression as Maximum Likelihood

Properties of Maximum Likelihood

statistic efficiency
parametric case

Bayesian Statistics

frequentist statistics, Bayesian statistics
prior probability distribution
Example: Bayesian Linear Regression
posterior

Maximum A Posteriori (MAP) Estimation

maximum a posteriori

Supervised Learning Algorithm

Probabilistic Supervised Learning

logistic regression

Support Vector Machines

kernel trick
kernel
Gaussian kernel
radial basis function
template matching
kernel methods
support vectors

Other Simple Supervised Learning Algorithms

decision tree

Unsupervised Learning Algorithm

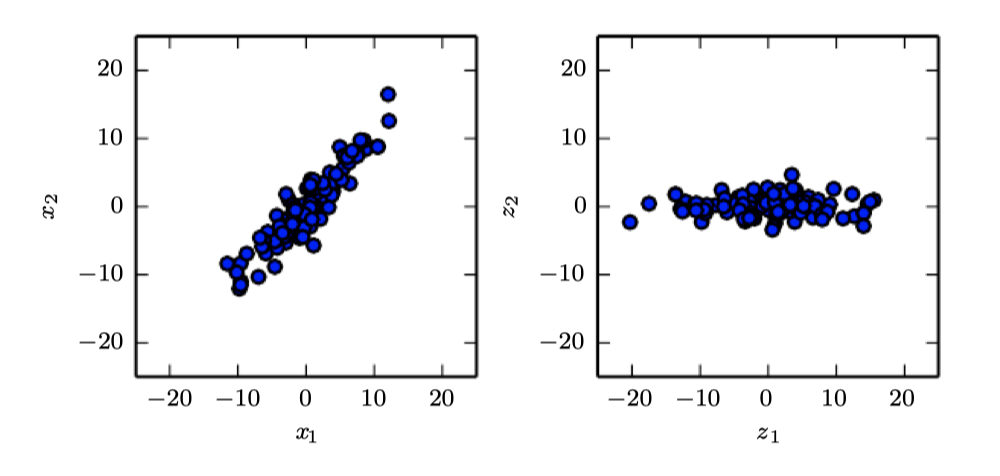
Principal Components Analysis

k-means Clustering

Stochastic Gradient Descent

stochastic gradient descent
minibatch

Building a Machine Learning Algorithm

Challenges Motivating Deep Learning

• 이 장에서 설명하는 간단한 머신러닝 알고리즘은 다양한 중요 문제에 대해 매우 잘 작동하지만, 음성이나 물체 인식과 같은 AI의 핵심 문제를 해결하는 데 성공하지 못했고, 딥러닝의 개발은 이러한 문제가 모티브가 되었다.
• 이 섹션에서는 고차원 데이터로 작업할 때 새로운 예제에 대한 일반화의 문제가 어떻게 기하급수적으로 어려워지는지, 전통적인 머신러닝에서 일반화를 달성하는 데 사용된 메커니즘이 고차원 공간에서 복잡한 함수를 학습하기에 어떻게 불충분한지에 대해 설명한다. 또한 이러한 공간은 종종 높은 계산 비용을 필요로 한다. 딥러닝은 이러한 문제들을 극복하기 위해 설계되었다.

The Curse of Dimensionality

• 데이터의 차원 수가 많을 때 많은 머신러닝 문제는 매우 어려우며 이를 차원의 저주(curse of dimensionality)라고 한다. 특히 변수의 수가 증가함에 따라 possible distinct configurations of a set of variables의 수가 기하급수적으로 증가한다는 점이다. 차원의 저주는 컴퓨터 과학의 여러 곳에서 발생하며 특히 머신러닝에서 일어난다.

데이터의 차원 수가 증가하면, 관심있는 configurations의 수가 기하급수적으로 증가 할 수 있다.

• (1) 1차원 예제에서는 1개의 변수를 10개의 관심영역을 구별하고자 한다. 이러한 각 영역에 포함되는 충분한 샘플을 통해 학습 알고리즘이 쉽게 일반화를 할 수 있다. 일반화하는 방법은 각 영역 내에서 목표 함수의 값을 추정하는 것이다.
• (2) 2차원 예제에서는 각 변수의 10가지 다른 값을 구별하는 것이 더욱 어렵다. 최대 $10*10=100$개의 지역을 확인해야 하며, 최소 그 지역을 커버할 정도의 많은 샘플이 필요하다.
• (3) 3차원 예제에서는 $10^3=1000$개의 지역으로 증가한다.
• [결론] $d$차원에서 각 축에서 $v$개의 값이 구별되기 위해서는 $O(v^d)$ 지역과 샘플이 필요하며, 이는 차원의 저주에 해당한다.

• 대표적으로 통계적인 어려움이 있다. $\bm{x}$의 possible configurations의 수가 훈련 샘플보다 훨씬 많기 때문에 통계적 문제가 발생한다.
• 이 문제를 이해하기 위해서 입력 공간이 그림과 같이 격자로 구성되어 있다고 생각해보자. 저차원 공간은 데이터에 의해 대부분 차지되는 적은 숫자의 격자 셀로 표현할 수 있다.
• 새로운 데이터 점들로 일반화시킬 때에는 새 입력값과 동일한 셀에 있는 학습 데이터를 확인할 수 있다.
  • 예를 들어 어떤 점 $\bm{x}$의 확률 밀도를 추정하는 경우, $\bm{x}$와 동일한 단위 부피 셀에 있는 학습 데이터 수를 총 학습 데이터 수로 나누면 된다.
  • 만약 분류를 한다면, 동일한 셀에 있는 학습 셋에서 가장 많은 클래스를 반환하면 된다.
  • 회귀를 할 경우, 해당 셀에서 관찰된 값의 평균을 낼 수 있다.
• 그러나 만약 본 적이 없는 데이터는 어떻게 해야할까? 고차원 공간에서 configurations의 수는 많기 때문에 일반적인 격자 셀은 학습 데이터셋이 없다. 따라서 새로운 configuration에 대해서는 의미있는 결과를 말할 수 있다. 기존의 많은 머신러닝 알고리즘은 단순히 새로운 지점의 출력값이 가장 가까운 학습 데이터 지점에서의 출력값과 거의 동일해야한다고 가정한다.

Local Constancy and Smoothness Regularization

smoothness prior, local constancy prior

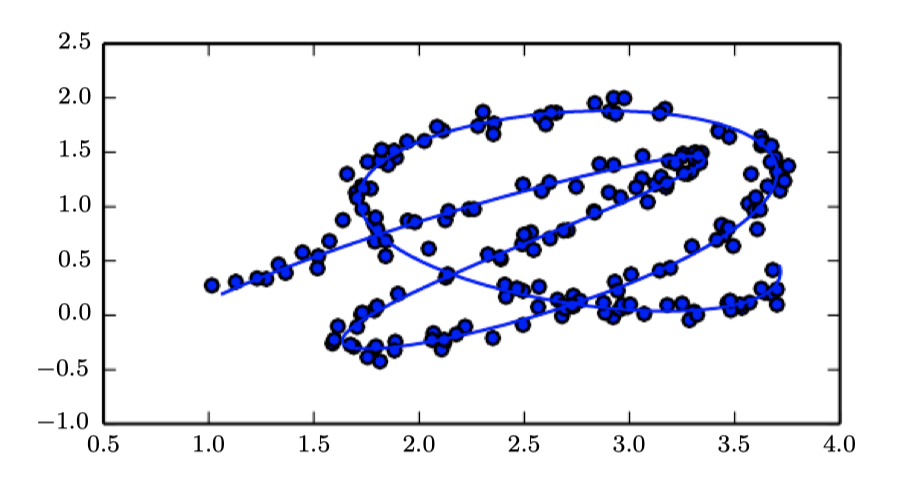
Manifold Learning

manifold
manifold learning
manifold hypothesis