[SUMMARY]
SPSS에서 단순회귀분석 해보기
[단순회귀분석 방법 순서도]
가설 수립
▼
산점도 그리기
▼
영향점 진단
▼
잔차 분석
▼
회귀모형 분석
[단순회귀분석]
(Simple Regression Analysis)
※ 출처:
시대고시 사회조사분석사 2급 실기 연습용 데이터
가구의 소득과 지출을 조사한 단위는 십만원인 자료가 있다.
소득을 독립변수로 하고 지출을 종속변수로 하는 단순회귀분석을 수행해 보자.
[1. 가설 수립]
먼저 가설을 수립한다.
1) 귀무가설: 소득은 지출에 영향을 미치지 않는다.
2) 대립가설: 소득은 지출에 영향을 미친다.
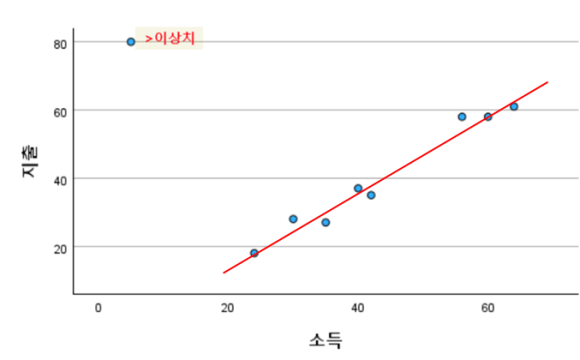
[2. 산점도 그리기]
산점도 그래프를 통해 확인할 사항은 크게 두 가지이다.1) 선형관계 확인으로 데이터 값들이 가상의 직선 주위에 몰려 있는지 살펴본다.
2) 이상치를 체크하고 영향점 여부를 확인하는 것이다.그래프-산점도/점도표 순으로 클릭
단순 산점도 클릭하고 정의 클릭
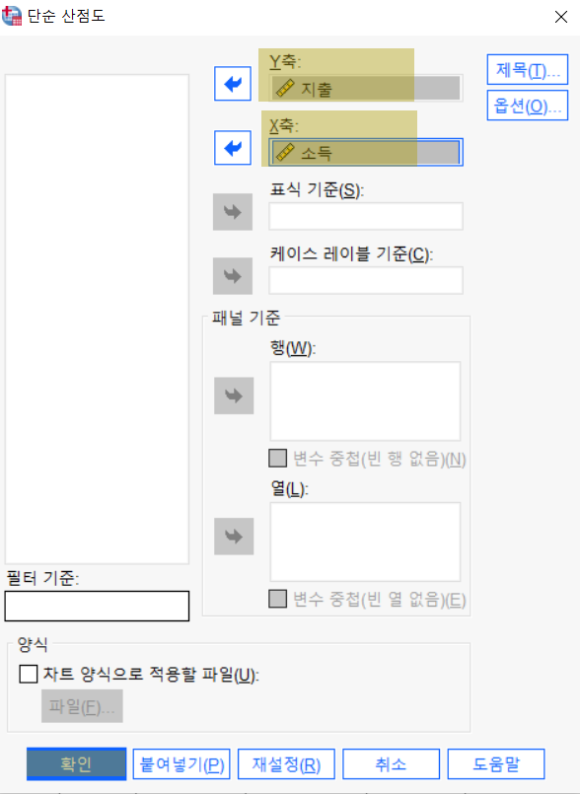
왼쪽 변수 목록에서 파란 화살표를 이용해
X축은 독립변수로 설정한 소득을 Y축은 종속변수로 설정한 지출로 설정한다.
확인 클릭
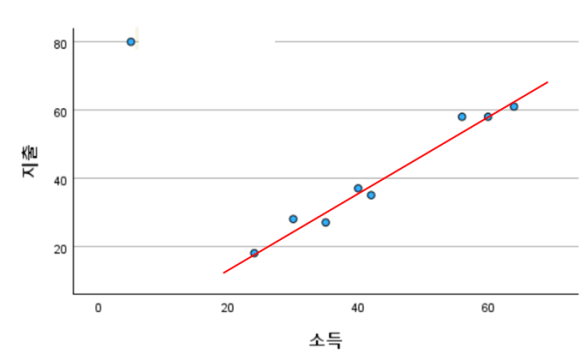
그러면 위와 같은 그래프가 나온다.먼저 데이터 값들 사이 가상의 선을 그어
데이터들이 선 가까이에 몰려 있는지 살펴본다.선에서 가까이 몰려있을수록 선형관계가 높게 나온다.
[3. 영향점 진단]
아까 산점도 그래프에서 왼쪽 위를 보면
값 하나가 다른 값들에 비해 혼자 떨어져 있는 것이 보인다.이것을 이상치(Outlier)라고 한다.
이 값이 회귀직선 기울기 변화에 영향을 미치면
영향점(Influential Point)이 되어 회귀분석에서 제외하면 안 된다.하지만 이 값을 제외하고 회귀분석을 해도 회귀직선 기울기에 큰 영향이 없다면
그냥 이상치가 되어 제거하고 회귀분석을 수행하도록 한다.그럼 이제 이 이상치 값이 영향점인지 알아보자.
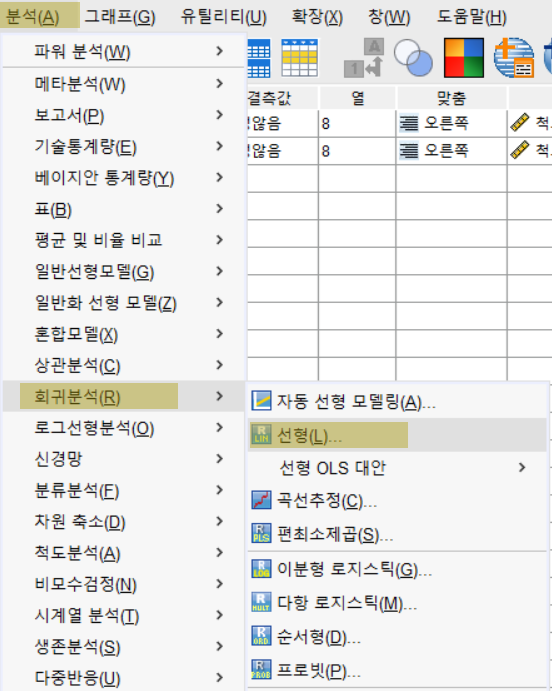
이상치 값을 포함한 회귀분석과 이상치 값을 제거한 회귀분석을 각각 수행해 보자.분석-회귀분석-선형 순으로 클릭
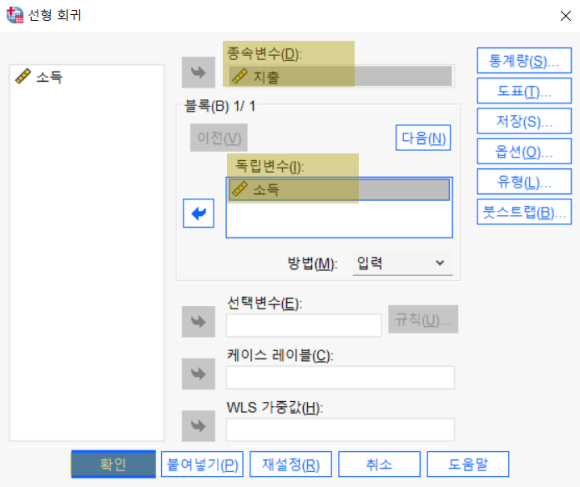
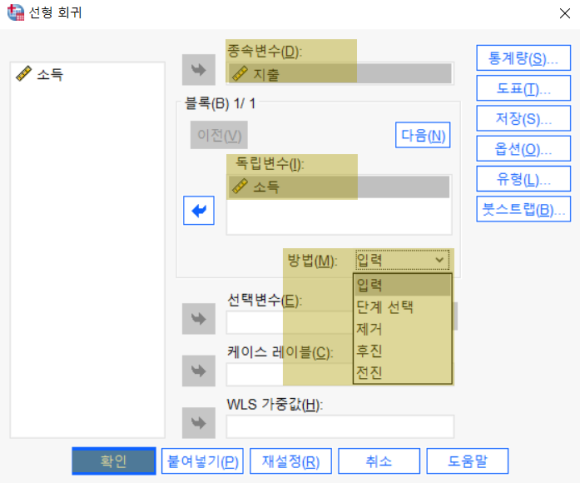
왼쪽 변수 목록에서 파란 화살표를 이용해
지출 변수를 종속변수로 소득을 독립변수로 이동시킨다.
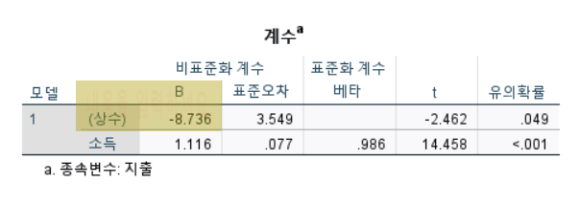
그러면 이 결과표에서
비표준화 계수의 상수 B 값이 회귀직선의 기울기 값이다.이상치를 포함하여 회귀분석을 실시한 B 값과
이상치를 제거하여 회귀분석을 실시한 B 값이
별 차이가 없으면 이상치가 되어 제거하고 회귀분석을 수행하면 된다.만약 차이가 많이 난다면
이상치는 영향점이 되어 이 값을 포함해서 회귀분석을 수행한다.정리하면,
1) 상수 B 값에 차이가 작다→기울기 영향 안 미침→이상치→제거하고 회귀분석
2) 상수 B 값에 차이가 크다→기울기 영향 미침→영향점→포함하여 회귀분석
[4. 잔차분석]
잔차들이 ±2보다 크면 이상치일 가능성이 높다.
이 범위 안에 데이터값들이 있어야 한다.분석-회귀분석-선형 순으로 들어가서 나타나는 대화상자에서 오른쪽에 도표 클릭
왼쪽 목록에서 파란 화살표 이용해서
ZRESID는 Y로 이동, ZPRED는 X로 이동
계속 클릭
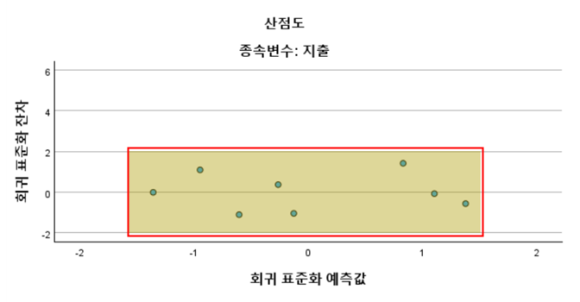
여기서 확인을 클릭하면 잔차 분석을 이용한 산점도가 나타난다.
잔차 분석에는 데이터 값들이 퍼져있는 모양에 따라 4가지 종류가 있다.
나중에 자세히 정리하기로 하자.일단 여기서 데이터값들이 옆으로 길쭉한 직사각형 모양으로 분포하고 있어야
등분산성에 문제가 없어 회귀분석을 수행할 수 있게 된다.
[5. 회귀모형 분석]
이제 위에서 이상치로 찾은 값들은 데이터 선택 기능을 이용해
제외하고 회귀분석을 수행하면 된다.
분석-회귀분석-선형 순으로 클릭
회귀분석에서는 방법을 5가지 중에 정할 수 있다.
각자 연구 설계에 맞게 설정하면 된다.
이 부분은 다중회귀분석에서 자세히 알아보도록 하자.다음으로 확인 클릭하면 결과표가 나타난다.
[결과 해석]
여기서는 회귀모형의 적합성을 살펴본다.회귀모형의 적합성인 결정계수 R제곱 값이 0.972이다.
회귀식에 의해 설명되는 비율이 97.2%이다.결정계수는 회귀모형이 좋은 모형인지를 설명해 준다.
결정계수 R제곱의 값이 1에 가까울수록 좋은 모형이라고 한다.좋은 모형이라는 것은 모든 표본 관측치가
추정된 회귀직선 위에 있다는 것을 의미한다.
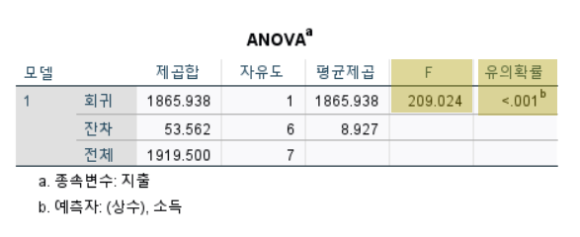
여기서는 회귀모형의 유의성을 검정한다.먼저 가설을 설정해 보자.
1) 귀무가설: 회귀모형은 유의하지 않다.
2) 대립가설: 회귀모형은 유의하다.검정통계량 F값이 209.024이고
유의확률 값이 0.000으로 유의수준 0.05보다 작기 때문에 귀무가설을 기각한다.즉, 회귀모형은 유의하다.
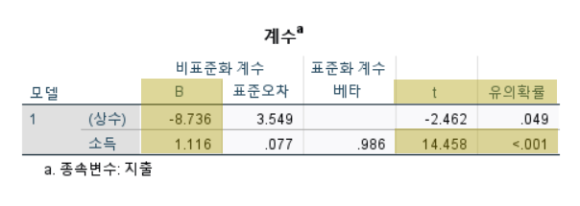
여기서는 회귀계수의 유의성을 검정하고, 회귀식을 얻을 수 있다.먼저 가설을 설정한다.
1) 귀무가설: 소득은 지출에 영향을 미치지 않는다.
2) 대립가설: 소득은 지출에 영향을 미친다.상수 줄 말고 독립변수인 소득 변수 줄의 값을 살펴본다.
검정통계량 t 값이 14.458이고
유의확률 값이 0.000으로 유의수준 0.05보다 작기 때문에 귀무가설을 기각한다.즉, 소득은 지출에 영향을 미친다.
비표준화계수 B 값을 이용해 회귀식을 추정할 수 있다.
추정된 회귀식은 y = -8.736+1.116χ회귀계수 b의 의미는 소득이 1단위(십만원) 증가할 때
지출은 1.116(십만원) 증가한다는 것을 의미한다.