이진법(binary)

이진법이란 ?

0과 1로만 표현한 수

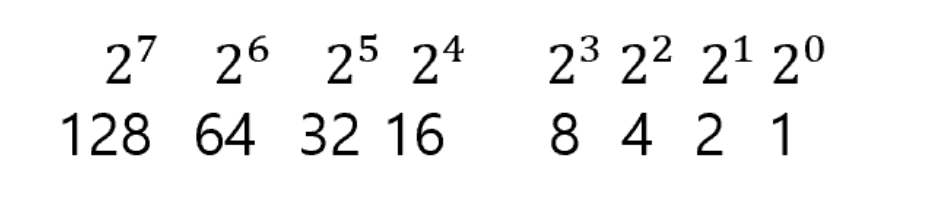
0000 0000  # 0  
0000 0001  # 1
0000 0010  # 2
0000 0011  # 3

프로그래밍에서 왜 2진법을 알아야 하는가 ?

오류의 최소화와 효율성(비용, 시간) 때문

이진법 연산자

비트연산자 소개

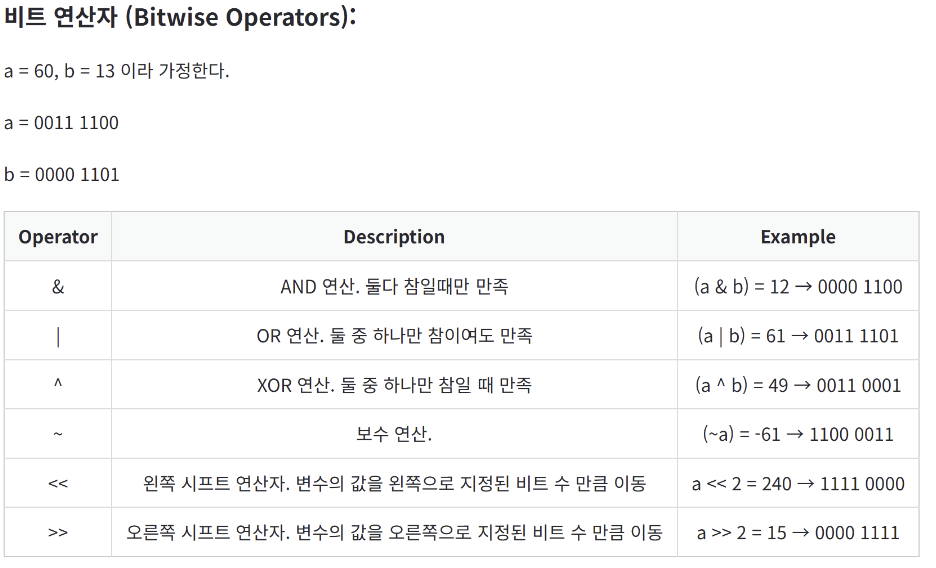
📌 참고
1 << k 는 1(20)을 k번 미는것과 같음
1 << 0 은 0001 1(10)
1 << 1 은 0010 2(10)
1 << 2 는 0100 4(10)
1 << 3 은 1000 8(10)
즉, 1 << k는 2 k와 같음

비트연산 활용

• 홀짝 비교
• 2의 제곱수인지 확인하기
• 2진수에서 1의 개수 찾기
• 비트마스킹 개념 이용한 알고리즘 풀이 (비트를 이용하여 집합을 표현, 처리)
  • 다빈치코딩알고리즘
• 실무에서는 임베디드, 통신 프로토콜, 암호화 등에 자주 사용 (빠르기때문에 성능이 중요한 시스템에 자주 사용)

#홀짝구분하기
def b(num) :
    if num & 1 == 0 :
        print('짝수')
    elif num & 1 != 0 :
        print('홀수')

def x(num):
    if num % 2 == 0 :
        print('짝수')
    elif num % 2 != 0 :
        print('홀수')

num=5
b(num)
x(num)



#2의 제곱수인지 확인하기
def is_exp_binary(n):
    return print(n & (n - 1) == 0)

is_exp_binary(5)

'''
#5
0101 & 0100 = 0100
#4
0100 & 0011 = 0000
'''


#2진수에서 1의 개수 찾기
def bit_count(n):
    k = 0
    count = 0

    while n >= (1 << k):
        if n & (1 << k) != 0:
            count += 1
        k += 1

    return count

n=3
print(bin(n))
print(bit_count(n))
'''
0011 & 0000  0000
count = 0
k = 1

0011 & 0001  0001 
count =1 
k = 2

0011 & 0010  0010 
count = 2
k = 3

0011 & 0011  0011
count = 2
k = 4
'''

def forin(c) :
    answer = 0
    a= bin(c)[2:]
    for i in a :
        if i == '1' :
            answer += 1
        
    return answer

print(forin(3))

오늘의 문제

프로그래머스-1차 비밀지도

문제 선택 이유

기업의 코테는 어떤 수준인지 궁금했고 , 비트연산자 개념 적용이 어려워서 찾아봤습니다

이번 문제에서 사용한 함수, 연산자

• bin(num)
  

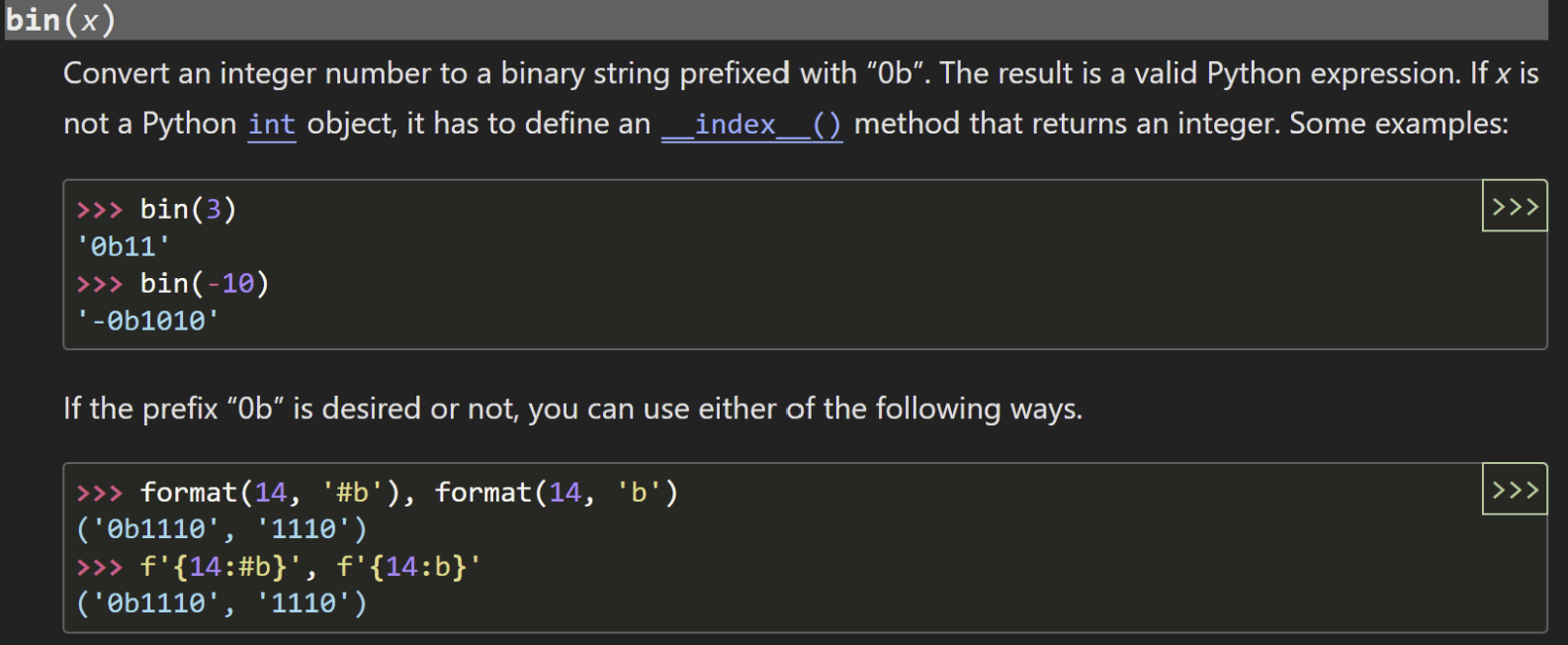
  • bin(num)[2:] (슬라이싱을 활용하여 이진수만 사용)

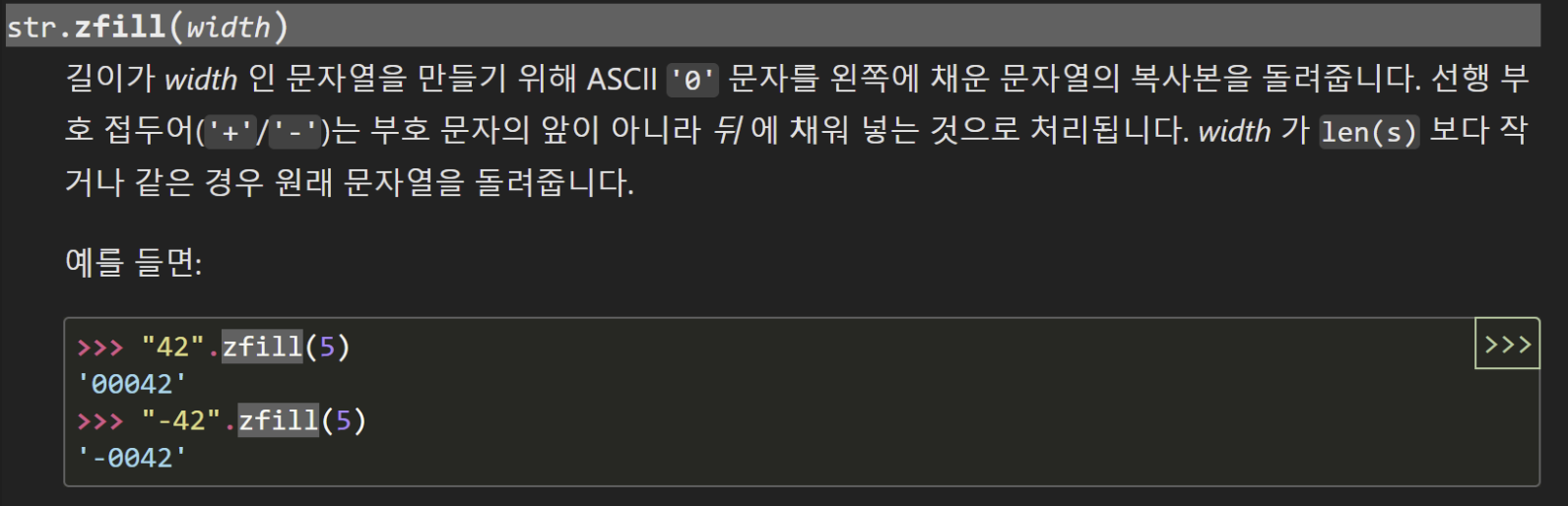
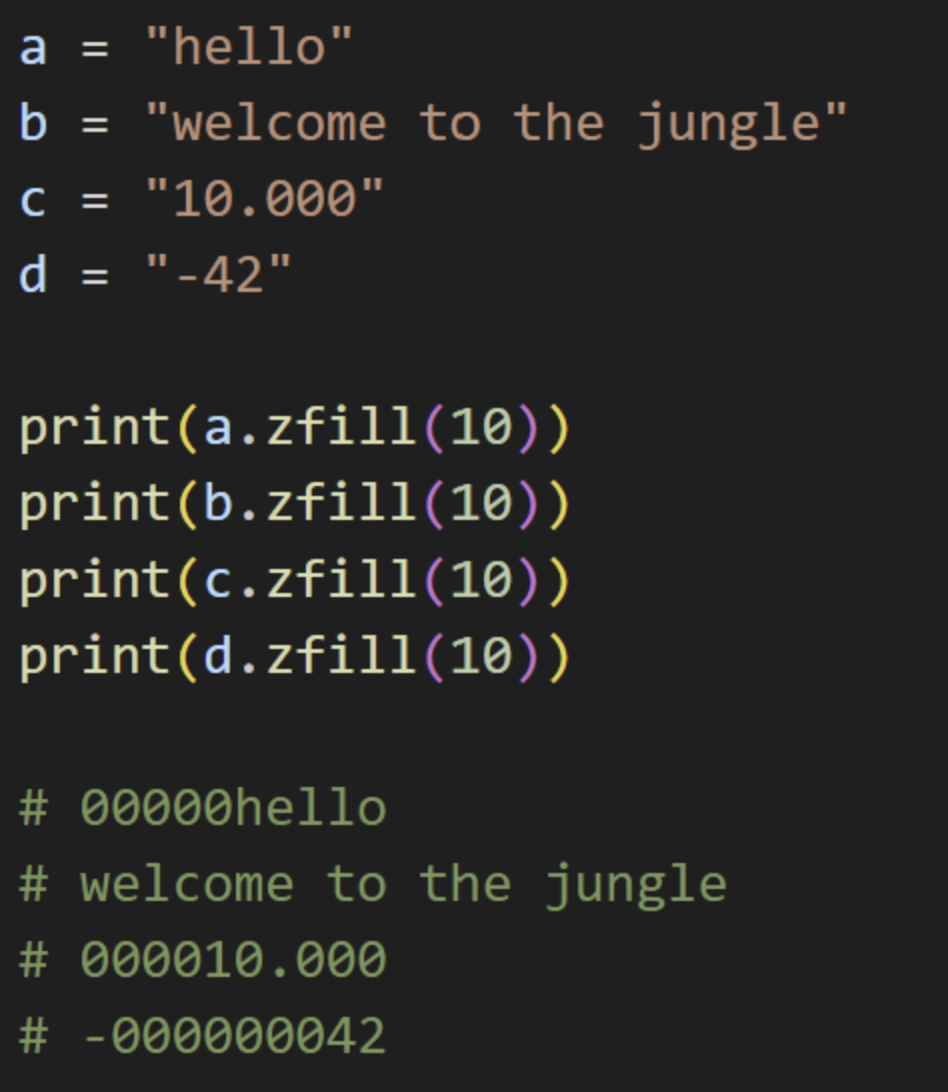
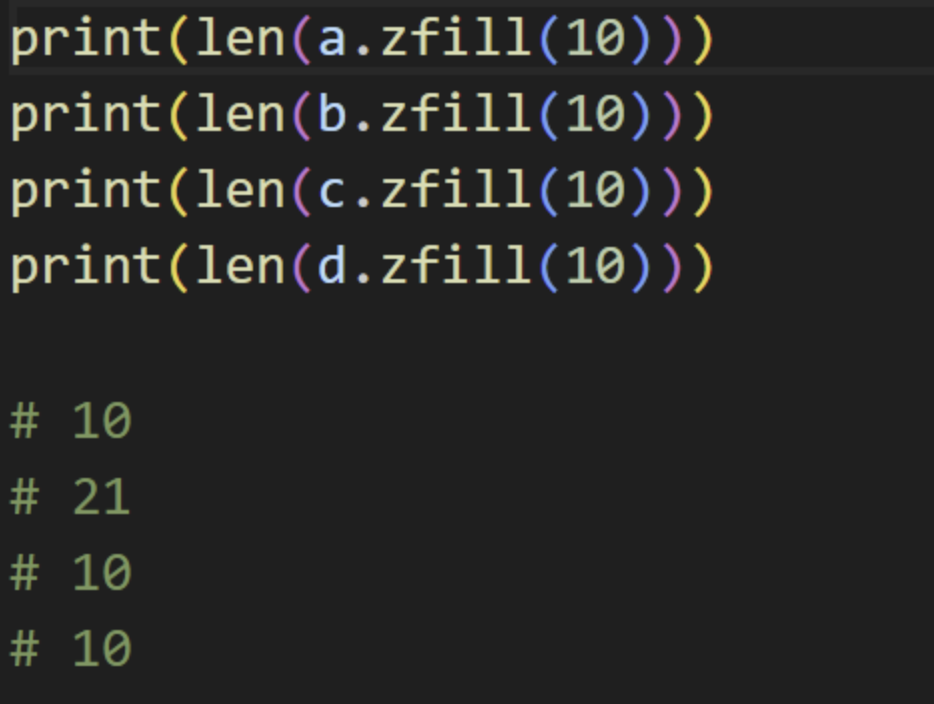
• .zfill(num)
  Python String zfill() Method
  
  
  

• | 연산자 (or 연산자)

문제 접근 방법

1. 비트연산이 필요하다 -> or 연산자가 필요(|)
2. 비트연산 값을 이진법으로 변환
3. n의 길이만큼 0으로 채우기
4. 이진법에서 1을 #으로, 0을 공백으로 대체
   
   
   

내 코드

def solution(n, arr1, arr2):
    answer = []
    for i in range(n) :
        answer.append((bin(arr1[i] | arr2[i])[2:].zfill(n)).replace('1', '#').replace('0', ' '))
    return answer