[알고리즘] 백준 - 2477 ( 참외밭 ) / JAVA

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class 실험실 {
	
	public static void main(String[] args) throws Exception{
		BufferedReader br =new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		int K = Integer.parseInt(st.nextToken()); // 참외
		
		int max = 0;
		int sum = 0;
		
		st = new StringTokenizer(br.readLine());
		st.nextToken();
		int a = Integer.parseInt(st.nextToken()); //첫번째 변은 마지막 변과 곱해주어야 하므로 따로 처리
		int before = a;
		
		for(int i = 1 ; i < 6 ; i++) {
			st = new StringTokenizer(br.readLine());
			st.nextToken();
			int now = Integer.parseInt(st.nextToken());
			max = Math.max(now*before, max); // 최댓값은 인접한 변의 곱 중 하나이다.
			sum += now*before;
			before = now;	
		}
		sum+= a*before; // 마지막 변과 첫번째 변 곱해줌
		max = Math.max(a*before, max); // 마지막변과 첫번째 변 크기 체크
		
		
		int result = (max- (3*max - sum))*K;  // 3*max - sum : 빈 부분의 넓이
		System.out.println(result);
	}
}

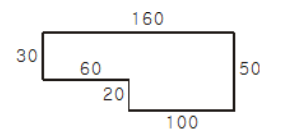
위와 같은 도형이 있다고 할 때 인접한 변들을 계속해서 곱해본다고 생각하면 다음과 같다.

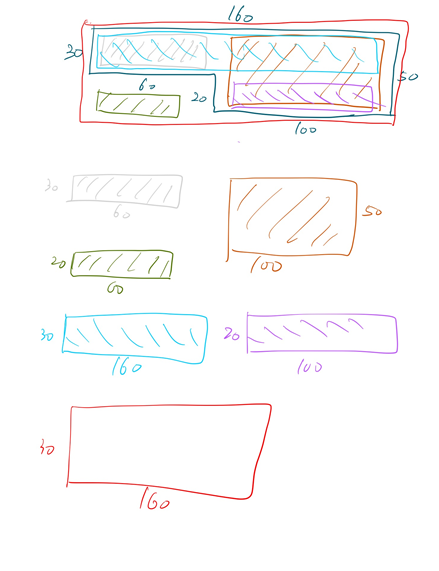
여기서 규칙을 하나 찾을 수 있는데 4부위로 나누어서 보면
1사분면(100x30) 은 하늘색 , 갈색 , 빨간색 3부분이 겹친 것을 확인할 수 있고
2사분면(30x60) 은 회색 , 하늘색 , 빨간색 3부분이 겹친 것을 알 수 있다.
3사분면(60x20) 은 국방색 , 빨간색 2부분이 겹쳐있고
4사분면(100x20) 은 보라색 , 갈색 , 빨간색 3부분이 겹쳐있다.

이를 전부 더하면
$3*(1사분면) + 2*(2사분면) + 3*(3사분면) + 4*(4사분면) = 3*(전체 넓이) - 2사분면$

따라서 빈 부분의 넓이는
$3*(전체 넓이)-(인접한 변의 곱들의 합)$ 이다.