[Algorithm] 시간복잡도, 공간복잡도

📚 복잡도 (Complexity)

• 알고리즘의 성능, 효율성을 나타내는 척도
• 시간복잡도 (Time Complexity)와 공간 복잡도 (Space Complexity)로 나눌 수 있음
• 각 알고리즘이 주어진 특정 크기의 입력(n)을 기준으로 수행시간(연산) 혹은 사용공간이 얼마나 되는지 객관적으로 비교할 수 있는 기준을 제시
• 복잡도를 나타내는 방법으로는 점근 표기법으로 O(빅오) , Ω(오메가), Θ(세타) 등이 있고, 주로 빅오와 세타 표기법이 사용된다.

한마디로 정리하자면 어떤 알고리즘이 효율적인지를 판단하는 척도 라고 생각하면 된다.

⏰ 시간 복잡도 (Time Complexity)

시간 복잡도 란 특정 크기의 입력을 기준으로 할 때 필요한 연산의 횟수를 나타낸다. (알고리즘을 실행하여 종료할때까지 필요한 시간)

이름은 시간복잡도이지만, 실행 시간이 아닌 연산횟수를 세는 이유는 다음과 같다.

• 모든 OS, ODE, 플랫폼에서 동일한 결과가 나오지 않는다.
• 실행 시간 측정을 위한 또 다른 방법이 필요하다.

🏠 공간 복잡도 (Space Complexity)

공간 복잡도 란 프로그램 실행과 완료에 얼마나 많은 공간 (메모리)가 필요한지를 나타낸다.(알고리즘을 실행하여 종료할때까지 필요한 기억장치의 크기
)

알고리즘을 실행시키기 위해 필요한 공간(space)는 두가지로 나뉜다.

1. 알고리즘과 무관한 공간인 고정공간
   • 코드가 저장되는 공간
   • 알고리즘 실행을 위해 시스템이 필요로 하는 공간 등
2. 알고리즘과 밀접한 공간인 가변공간
   • 문제를 해결하기 위해 알고리즘이 필요로 하는 공간
   • 변수를 저장하는 공간
   • 순환 프로그램일 경우 순환스택 등

시간 복잡도 vs 공간복잡도

• 시간 복잡도는 얼마나 빠르게 실행되는지, 공간 복잡도는 얼마나 많은 자원(메모리 공간)이 필요한지를 판단한다.
• 시간 복잡도와 공간 복잡도는 반비레하는 경향이 있어, 보통 알고리즘의 성능을 판단할 때는 시간복잡도를 위주로 판단한다.

🅾️ 빅오 표기법 (Big-O notation)

빅오 표기법(Big-O notation) 은 복잡도를 나타내는 점근 표기법 중 가장 많이 사용되는 표기법이다.

• 빅오 표기법이 가장 많이 사용되는 이유는 알고리즘 효율성을 상한선 기준으로 표시하기 때문이다.
• 다시말해 최악의 경우를 고려하는데 가장 좋은 표기법이다.
  ➡️ 알고리즘 효율성은 값이 클수록 비효율적임을 의미한다.

📈 빅오 표기법의 수학적 정의

O(g(n)) = {f(n) : there exist positive constants c and $ n_0 $ such that 0≤f(n)≤cg(n) for all n≥$ n_0 $}

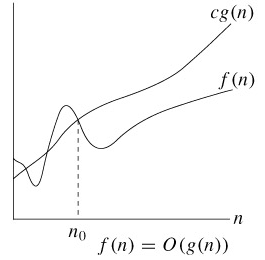
• n0를 기준으로 n0보다 오른쪽에 있는 모든 n값에 대해 함수 f(n)은 함수 cg(n)보다 같거나 작다는 의미이다. ( 점근적 상한선 )
• 빅오 표기법에서는 주어진 알고리즘이 아무리 나빠도 비교하는 함수와 같거나 좋다.
• 그래프가 아래에 있을 수록 수행시간이 짧으므로 성능이 좋은 것이다.

📝 빅오 표기법의 특징

1. 상수항 무시
   • 빅오 표기법은 n이 충분히 크다고 가정하고 있고, 알고리즘의 효율성은 n의 크기에 영향을 받으므로 상수항 같은 사소한 부분은 무시한다.
     ➡️ O(2n)은 O(n)으로 간주
2. 영향력 없는 항 무시
   • 빅오 표기법은 n의 크기에 영향을 받으므로 가장 영향력이 큰 항 이외에 영향력이 없는 항은 무시한다.
     ➡️ O(n^2 + 2n + 1 )은 O(n^2)로 간주

📑 시간복잡도와 빅오 표기법

시간 복잡도는 특정 크기의 입력(n)을 기준으로 실행하는 연산의 횟수이다.

➡️ 연산의 횟수를 세면 된다.

• 알고리즘이 실행 될 때의 모든 연산의 횟수를 세는 것 X
  ➡️ 알고리즘에서 핵심이 되는 연산의 횟수만 세면 된다.

다음은 시간복잡도와 그 예시를 나열한 것이다.

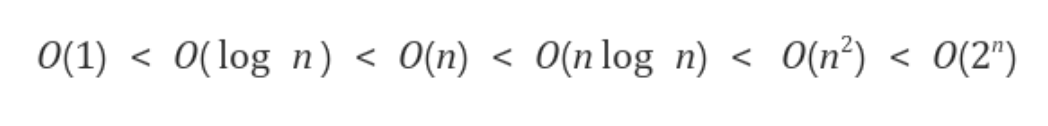
상수함수 < 로그함수 < 선형함수 < 다항함수 < 지수함수
왼쪽에서 오른쪽으로 갈 수록 성능이 떨어지며, 시간 복잡도가 좋지 않은 알고리즘이다.