https://leetcode.com/problems/perfect-rectangle/
Brute Force
이 문제을 봤을 때 가장 먼저 생각 나는 방법은
전체 좌표평면을 2d 배열로 나타내고 각각의 rectangle 에 대해서 색칠을 한 후에
이 전체 좌표평면이 rectangle 인지 확인하는 방법입니다.
하지만 이 방법은 매우 비 효율적이라는 것을 알 수 있습니다.
만약 [0,0,10**9, 10**9] 라는 rectangle 한개만 존재해도 Timeout 이 될테니까요.
Coordinate Compression
즉 보다 효율적인 방법을 생각해야 합니다.
그 중 한개로 Coordinate Compression(좌표압축) 기법을 사용할 수 있습니다.
입력 범위가 아무리 커도 입력의 갯수가 작다면 우리는 그 입력을 압축 시킬 수 있습니다.
좌표 압축에 대한 자세한 설명은 좌표압축 을 구글링 해주세요
밑의 코드는 좌표압축을 통해서 ys, xs 의 크기을 최대 O(N) 로 제한시킵니다.
밑의 코드의 시간복잡도는 O(N^3) 이 될 것 같습니다.
class Solution:
def isRectangleCover(self, rectangles: List[List[int]]) -> bool:
xs = []
ys = []
for y1, x1, y2, x2 in rectangles:
xs += [x1, x2]
ys += [y1, y2]
xs = sorted(list(set(xs)))
ys = sorted(list(set(ys)))
x_num_to_id = {num:i for i, num in enumerate(xs)}
y_num_to_id = {num:i for i, num in enumerate(ys)}
rectangles = [[y_num_to_id[y1],
x_num_to_id[x1],
y_num_to_id[y2],
x_num_to_id[x2]] for y1, x1, y2, x2 in rectangles]
h, w = len(ys), len(xs)
grid = [[0 for _ in range(w-1)] for _ in range(h-1)]
for y1,x1,y2,x2 in rectangles:
for y in range(y1, y2):
for x in range(x1, x2):
grid[y][x] += 1
return all(all(cell == 1 for cell in row) for row in grid)
Open Close
이제 조금 더 최적화을 해보죠.
위의 코드에서는 grid 에 색칠을 하는 것으로 rectangle 을 구분하였습니다.
이번에는 grid 을 직접 색칠하는 것이 아니라, grid 의 변화에 대해서만 고민해보죠.
만약 grid 을 아래에서부터 차근차근 읽어 올라간다고 해봅시다.
몇 개의 작은 rectangle 이 시작됩니다.
그 다음 줄에서 몇개의 rectangle 은 끝나지만, 몇개는 아직 유지되어 있습니다.
예를 들어서 예제의
rectangles = [
[1,1,3,3],
[3,1,4,2],
[3,2,4,4],
[1,3,2,4],
[2,3,3,4]
]
의 경우에는 1 번째 줄에서는 2개의 rectangle 이 시작되지만 2번째 줄에서는 1개의 길이 2짜리 rectangle 은 유지되면서 길이 1짜리 rectanlge 만 끝나고, 다시 새로운 길이 1 짜리 rectangle 이 시작됩니다.
즉 우리는 각 rectangle 을 매번 다시 볼 필요 없이 rectangle 의 변화에만 주목하면 됩니다.
밑의 코드는 rectangle 의 open, close 을 저장하고 그것을 update 합니다.
시간복잡도는 O(N^2) 이 됩니다.
class Solution:
def isRectangleCover(self, rectangles: List[List[int]]) -> bool:
xs = []
for _, x1, _, x2 in rectangles:
xs += [x1, x2]
xs = sorted(list(set(xs)))
x_num_to_id = {num:i for i, num in enumerate(xs)}
opens = collections.defaultdict(list)
closes = collections.defaultdict(list)
ys = set()
for y1, x1, y2, x2 in rectangles:
x1, x2 = x_num_to_id[x1], x_num_to_id[x2]
opens[y1] += [(x1, x2)]
closes[y2] += [(x1, x2)]
ys.add(y1)
ys.add(y2)
# 현재 색칠되어 있는 범위을 cur 로 표시합니다.
cur = set()
for y in sorted(ys)[:-1]:
for x1, x2 in closes[y]:
for x in range(x1, x2):
cur.remove(x)
for x1, x2 in opens[y]:
for x in range(x1, x2):
# 중복 발생
if x in cur:
return False
cur.add(x)
if len(cur) != len(xs)-1:
return False
return True
SortedList
위의 코드에서는 중복발생, 즉 rectangle 의 겹치는 것을 cur 이라는 set 을 통해서 했습니다.
이 과정때문에 O(N) 의 시간복잡도가 소모되었으나 이것을 보다 효율적으로 구해봅시다.
sortedList 을 통해서 x 좌표에 대한 정렬된 리스트을 유지합니다.
[(0,1),(3,-1),(3,1),(5,-1),(7,1),(8,-1)] 만약 sl 이 이렇게 되어있다면
현재 1~3, 3~5, 5~7, 7~8 의 rectangle 로 row 가 구성되어 있는 것을 알 수가 있습니다.
이 row 가 연속적이고, 시작과 끝이 s, e 라면 현재의 row 는 perfect rectangle 의 row 라고 생각 할 수 있습니다.
시작과 끝을 구하는 것은 매우 간단합니다.
row 가 연속적인지 아는 방법은 한번 순회하거나, 또는
- 전체 길이을 구하고
- 중복된 부분이 없다면
연속적이라고 판단할 수 있습니다.
전체 길이을 cur 로 구합니다.
그리고 중복된 부분은 bisect 을 통해서 구할 수 있습니다.
밑은 이것을 표현한 코드 입니다.
시간 복잡도는 O(NlogN) 이 됩니다.
from sortedcontainers import SortedList
class Solution:
def isRectangleCover(self, rectangles: List[List[int]]) -> bool:
opens = collections.defaultdict(list)
closes = collections.defaultdict(list)
s, e = min(x1 for _, x1, _, _ in rectangles), max(x2 for _, _, _, x2 in rectangles)
for y1, x1, y2, x2 in rectangles:
opens[y1] += [(x1, x2)]
closes[y2] += [(x1, x2)]
sl = SortedList()
ys = sorted(opens.keys() | closes.keys())
cur = 0
for y in ys:
for x1, x2 in closes[y]:
cur -= x2-x1
sl.discard((x1,1))
sl.discard((x2, -1))
for x1, x2 in opens[y]:
l, r = sl.bisect_left((x1, 1)), sl.bisect_left((x2, -1))
if l != r:
return False
sl.add((x1, 1))
sl.add((x2,-1))
cur += x2-x1
if ys[-1] != y and cur != e-s:
return False
if len(sl) == 0 and cur == 0:
return True
return False
Greedy 한 방법
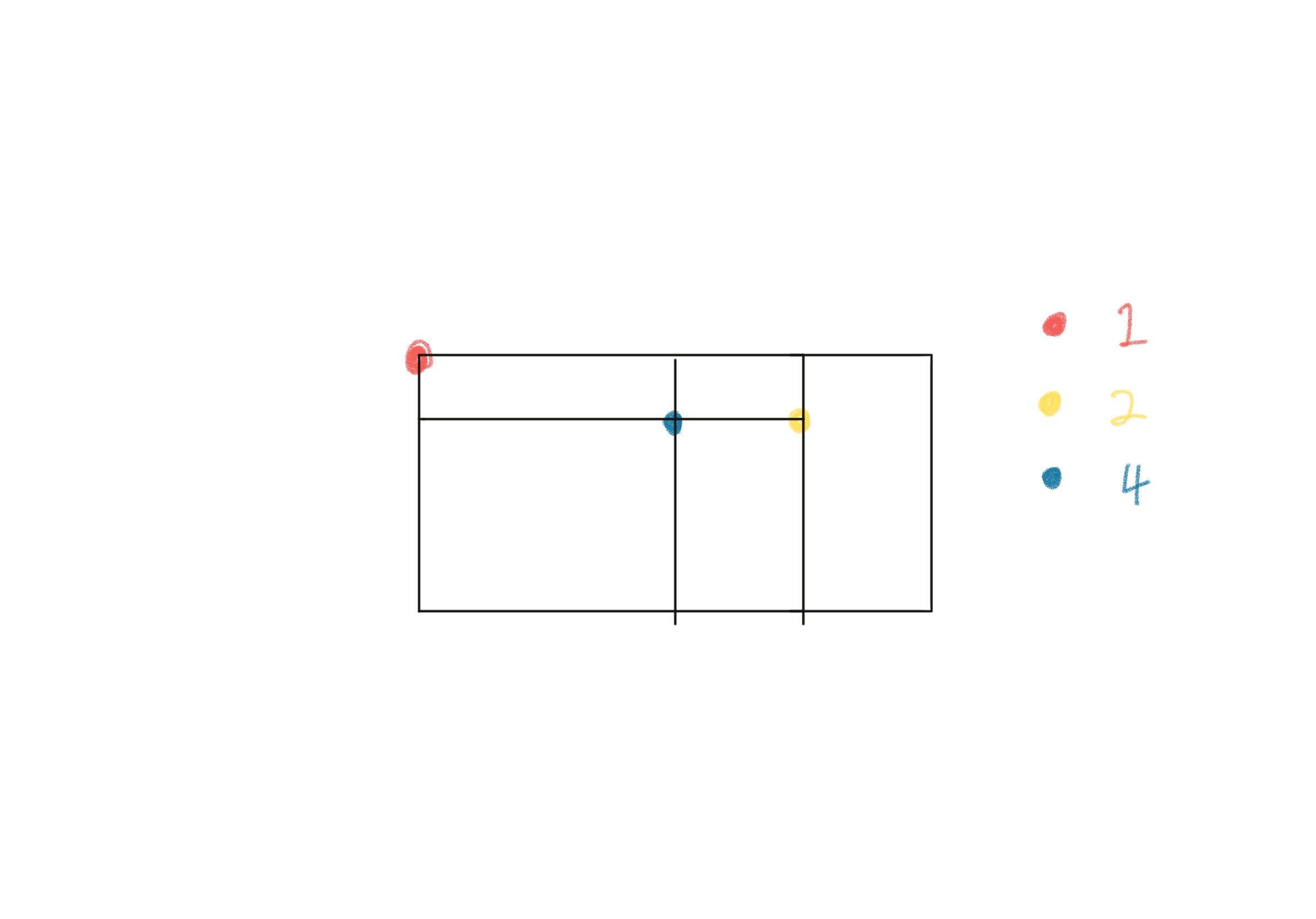
perfect rectangle 의 모든 점은 총 3가지로 구분이 됩니다.
- 1개의 rectangle 에만 속하는 점 (빨강)
- 2개의 rectangle 에 속하는 점(노랑)
- 4개의 rectangle 에 속하는 점 (파랑)
그리고 prefect rectangle 이 되기위해서는 빨강의 점은 4개여야 하고 이 점들이 perfect rectangle 을 구성하는 점이 됩니다.
그리고 각 rectangle 의 겹침을 방지 하기 위해서 각 rectangle 의 넓이의 합은 perfect rectangle 의 넓이와 같아야 합니다.
이러한 규칙을 통해서 만든 코드가 밑 입니다.
시간 복잡도는 O(N) 입니다. 개인적으로 이 방법은 매우 생각하기 어려운 방법 같습니다.
class Solution:
def isRectangleCover(self, rectangles: List[List[int]]) -> bool:
corners = collections.Counter()
L,B,R,U = float('inf'), float('inf'), float('-inf'), float('-inf')
area = 0
for l,b,r,u in rectangles:
area += (r-l)*(u-b)
corners[l, b] += 1
corners[l, u] += 1
corners[r, b] += 1
corners[r, u] += 1
L, B, R, U = min(L,l), min(B,b), max(R,r), max(U,u)
if area != (R-L)*(U-B):
return False
big_corner = [(L,B),(L,U),(R,B),(R,U)]
if not all(corners[k] == 1 for k in big_corner):
return False
if not all(corners[k]%2==0 for k in corners if k not in big_corner):
return False
return True