https://leetcode.com/problems/possible-bipartition/
N 명의 사람이 주어집니다. 각각의 아이디는 1,2,34, ... n 으로 표시합니다.
우리는 이 사람들은 2 그룹으로 나누고 싶습니다. 각 그룹의 사이즈는 상관없습니다.
각각의 사람들은 싫어하는 사람들이 있고 이러한 사람들은 같은 그룹 안에 있으면 안 됩니다.
숫자 N 과 dislike 가 주어질 때 2개의 그룹으로 나눌 수 있는지 체크하는 함수을 만드세요.
아이디어
모든 경우을 체크하는 방법이 있습니다.
이 경우 시간 복잡도는 O(2^N) 이 되기 때문에 너무 큽니다.
이 문제을 그래프로 생각해 볼까요?
dislike 을 edge 로 생각하고 사람들을 vertex 로 생각한다면 인접 노드 끼리 같은 색을 칠하지 않을 방법이 잇냐의 문제로 바꿉니다. 이때 색깔은 2가지만 존재하구요.
두가지 색깔을 red, black 이라고 해보죠. 서로 연결된 그래프 에서는 1개의 노드을 색칠 하는 순간 그 그래프의 모든 색깔이 정해집니다.
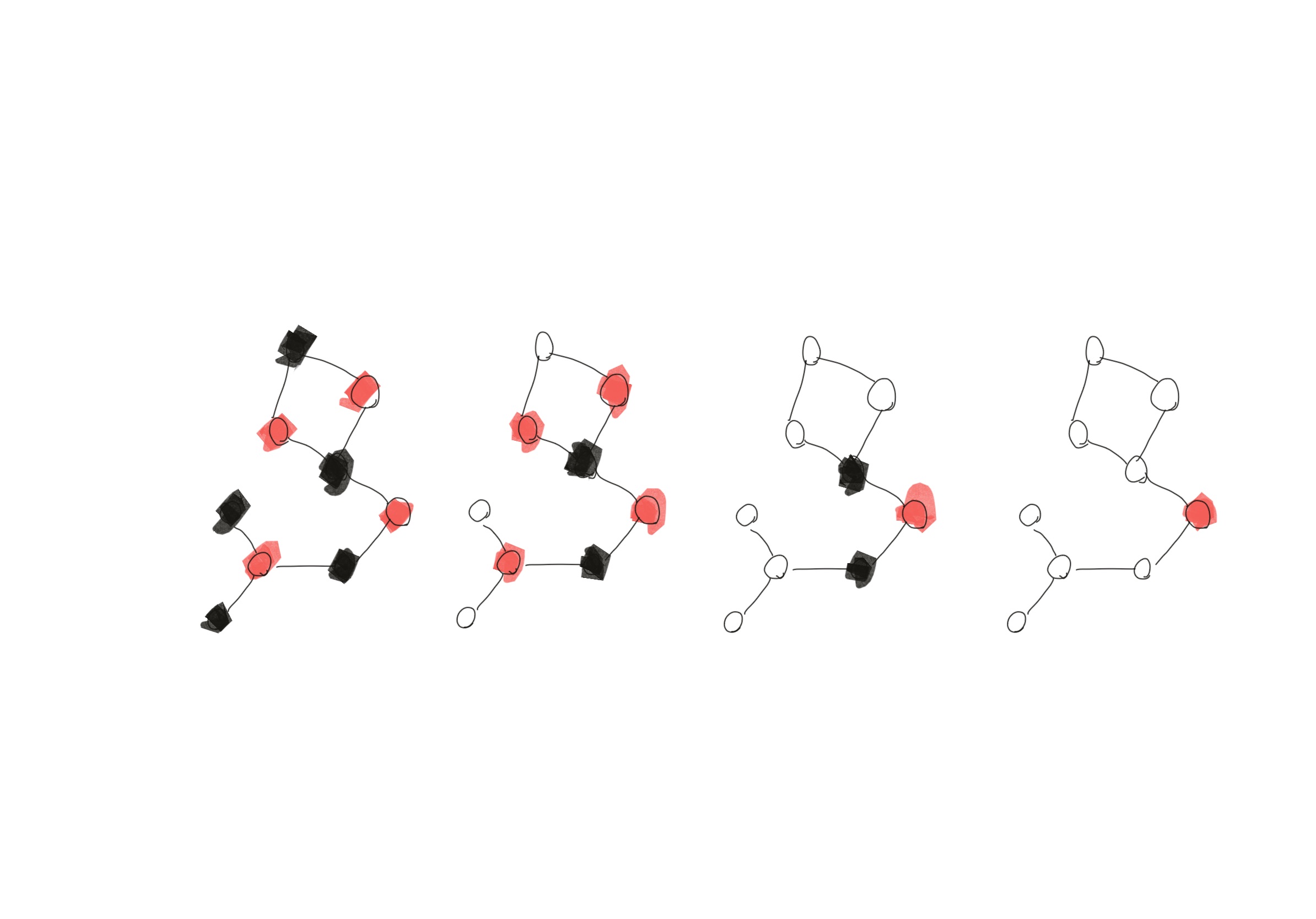
예를 들어서 위의 그림을 보죠. 어느 한점을 빨간색으로 색칠 하는 순간 인접 노드는 검정색을 칠해야만 하고, 다시 그 인접노드는 빨간색을 칠해야 하고, 결국 1개의 색칠된 그래프가 됩니다.
즉 그래프로 표현을 하고, 그 그래프의 노드 한개를 적당한 색깔 하나로 색칠하고 그 색깔을 지속적으로 전파하면 됩니다. 만약 전파 도중에 빨간색과 검정색이 동시에 존재해야하는 노드가 생긴다면 False 을 리턴하면 됩니다.
class Solution:
def possibleBipartition(self, N: int, dislikes: List[List[int]]) -> bool:
# 그래프로 표현합니다.
graph = collections.defaultdict(set)
for u, v in dislikes:
graph[u].add(v)
graph[v].add(u)
# 어떤 노드을 무슨색으로 칠했는지 저장합니다.
visited = dict()
# 모든 노드가 연결되어 잇다는 이야기가 없기 때문에 모든 노드에 대해서 BFS 을 해줍니다.
for i in range(1, N+1):
if i not in visited:
# BFS 을 합니다.
queue = collections.deque()
queue.append((i, 0))
while len(queue)> 0:
node, color = queue.popleft()
if node in visited:
# 두 가지 색깔이 상충한다면 False 을 리턴합니다.
if color != visited[node]:
return False
continue
visited[node] = color
for nxt in graph[node]:
queue.append((nxt, color^1))
return True전체 시간복잡도는 O(N+len(dislikes)) 가 됩니다.
