시퀀스 데이터

• 시퀀스(Sequence) 데이터란, 순차적으로 들어오는 데이터를 의미하며, event 발생 순서가 중요한 데이터다.
  • 소리, 문자열, 주가 데이터 등이 해당된다.
• 시퀀스 데이터는 독립동등분포(i.i.d.) 가정을 잘 위배하기 때문에 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포다 바뀌게 된다.
  • 개가 사람을 물었다 vs 사람이 개를 물었다. <- 매우 다르지 않은가?

즉, 과거 정보를 고려하여 미래를 예측해야 한다. 어떻게 해야할까?

---

시퀀스 데이터를 다루는 방법

방법 1. 조건부확률

즉, 초기시점 s=1부터 바로 직전의 과거 정보인 s-1 시점까지의 정보를 사용해서 현재 시점인 $X_{s}$를 모델링하는 방법이다.

그러나, 조건부확률을 활용한 예측은 문제가 있다. 과거의 모든 정보를 활용하여 시퀀스 데이터를 분석한다는 점이다. 사실 우리는 이렇게 모든 정보가 필요하지는 않는데 말이다. 예를 들어, 어떤 기업의 주가 예측 시, 이 기업의 30년전 데이터까지는 필요하지 않다. 최근 5년 데이터가 가장 중요한 것처럼 말이다.

해결책 1.
이에 대한 첫번째 가장 직관적인 해결책은 과거의 모든 data, t개의 정보를 모두 사용하는 것이 아니라, 고정된 길이 $\tau$ 만큼의 시퀀스만 사용하는 것이다. 이를 Aggressive Model (자기회귀모델): AR($\tau$) 라고 부른다.

해결책 1의 문제점.
그러나 이 방법의 문제는 $\tau$가 hyperparameter라는 것이다. 즉, $\tau$를 지정하기 위해 우리는 사전지식이 있어야할 수도 있고, 문제에 따라서 $\tau$가 가변적으로 변해야할 수도 있다. 우리는 과거 정보를 적절히 알아서(정보의 중요도에 따라 다르게?) 처리하는 다른 방법이 필요하다. 이름하여 RNN!

방법 2. RNN

다른 방법은 바로 이전 정보를 제외한 나머지 정보를 $H_{t}$라는 잠재변수로 인코딩하여 활용하는 잠재 AR 모델이다.

---

RNN 이해하기

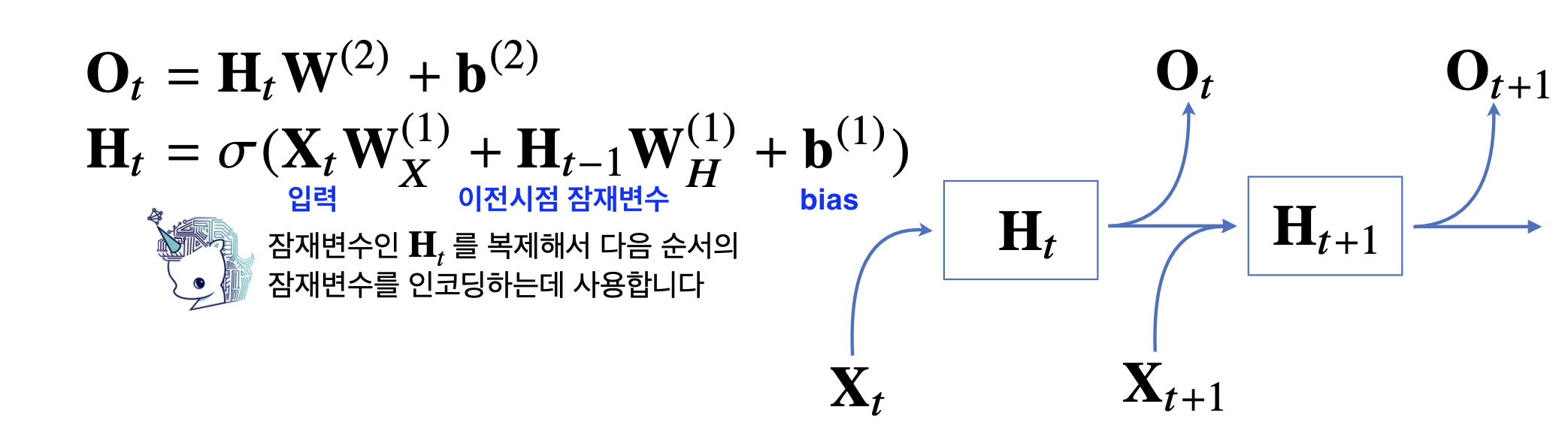
가장 기본적인 RNN 모형

1. 가중치행렬은 시점에 상관없이 (첫번째 시점은 데이터에 곱하던, 두번째 시점의 데이터에 곱하던 상관없이) 공유한다.

2. 가중치행렬은 3개이다. 다시 말하지만, 이 가중치는 t에 따라 변하는 것은 아니다.

   • $W_{x}^{(1)}$: 입력 $\rightarrow$ 잠재변수
   • $W_{H}^{(1)}$: 이전시점 잠재변수 $\rightarrow$ 현재시점 잠재변수
   • $W_{x}^{(2)}$: 잠재변수 $\rightarrow$ 출력

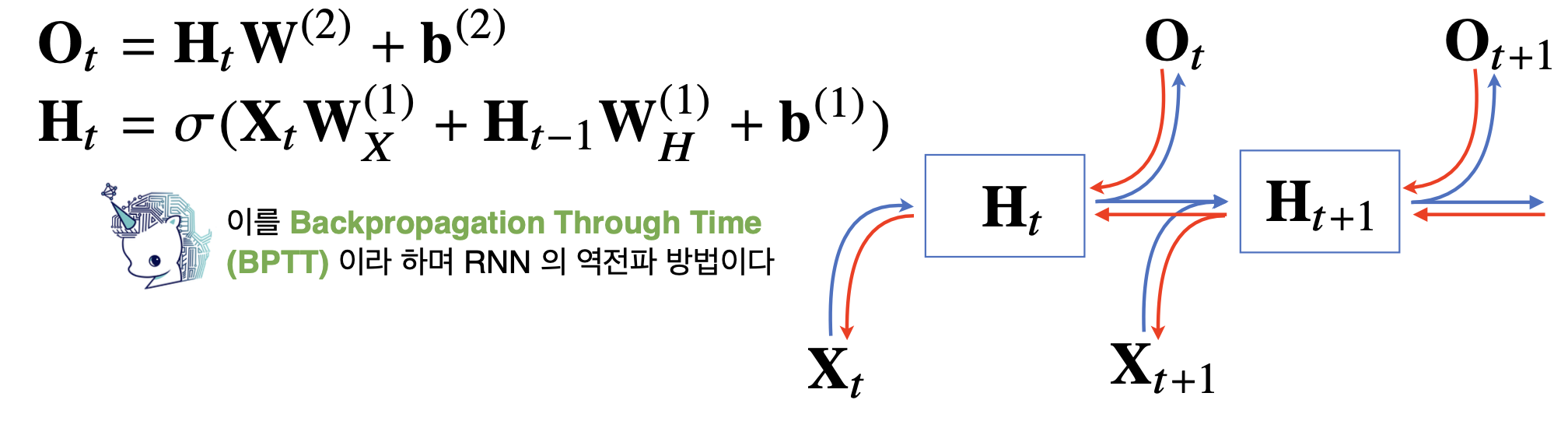
RNN의 Backpropagation

RNN의 역전파는 잠재변수의 연결그래프에 따라 순차적으로 계산한다. 이를 Backpropagation Through Time (BPTT)라고 한다.

왜 시퀀스 길이가 길어질수록 gradient 값이 불안정해질까?
가중치행렬 결과 값을 보면, gradient 값을 모두 곱해주는 형태이다. 따라서 현재시점부터 t까지의 길이가 길어질수록 gradient 값이 1보다 크면 전체적인 값이 크게 커지고, 1보다 작으면 전체 값이 매우 작아지게 된다. 즉, 미분값이 엄청 커지거나 작아질 확률이 높아진다. 즉, 일반적인 BPTT를 모든 시점에 적용하면 RNN학습이 불안정해지기 쉽상이다.

무엇보다 gradient vanishing 문제가 커지게 된다. 이는 문장의 길이가 긴데 과거의 정보가 중요한 데이터의 경우 더욱 큰 문제가 된다. 따라서 우리는 중간에 끊어주는 truncated BPTT를 만들었다.

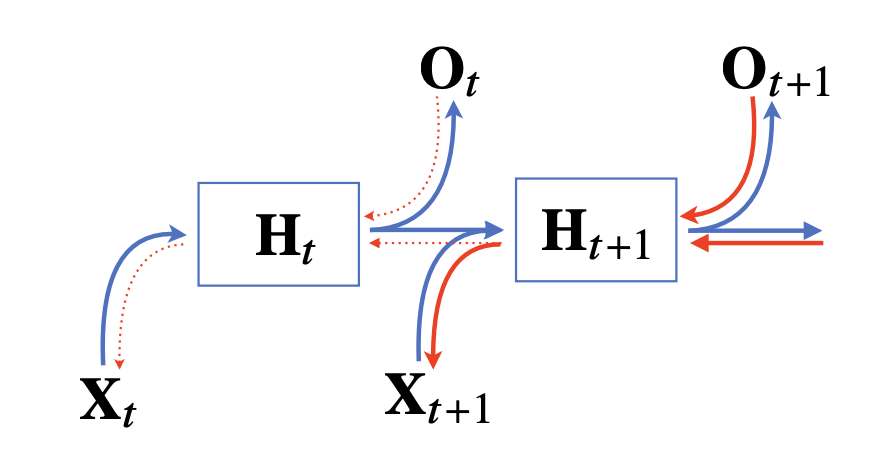
그런데 이것만으로도 완벽히 해결되지 않았다. 이를 해결하기 위해 등장한 것이 LSTM과 GRU이다. 이는 나중에 설명하도록 하겠다.