아래 내용은 네이버 AI precourse 강의를 개인 공부를 위해 정리한 내용입니다.

순한맛

미분과 경사하강법

• 미분값을 빼면 함수의 극소값의 위치를 구할 수 있으며, 경사하강법(gradient descent)라고 함.
• 경사 하강 방법은 극값에 도달하면 움직임을 멈춤.
• 따라서 경사하강법은 손실함수(loss function)의 최소값을 찾기 위해 사용함.
  • $w \leftarrow w - \lambda \frac{dL}{dw}$
  • 여기서 $\lambda$는 학습율이며, $\frac{dL}{dw}$은 손실함수$L$에서의 가중치$w$의 기울기를 의미한다.

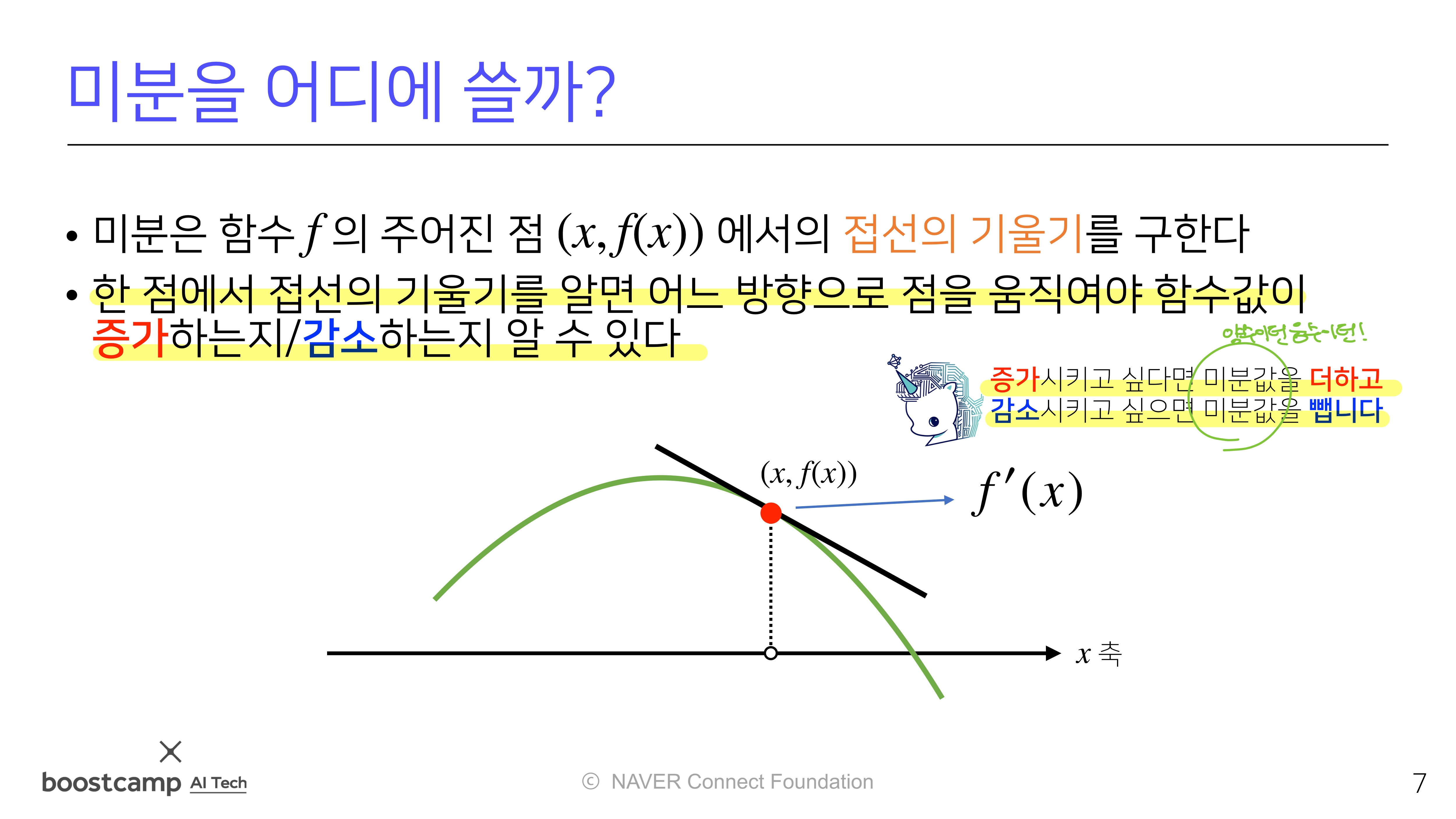
다변수 함수의 미분

• 각 변수 별로 편미분을 계산한 그레디언트(gradient) 벡터 이용
  • d차원의 vector이면 편미분을 d번 수행
  • 그레디언트 벡터는 각 점에서 가장 빨리 증가하는 방향으로 흐름
  • - 그레디언트 벡터는 각 점에서 가장 빨리 감소하는 방향으로 흐름

매운맛

선형회귀에서의 경사하강법

• 기존에는 Moore-Penrose 역행렬을 이용하여 적절한 선형모델을 구했는데, 이번에는 경사하강법을 이용하여 적절한 선형모델을 구해보자!
  • 이는 추후 선형모델이 아닌, 일반적인 모델에서의 최적화에서도 사용할 수 있을 것이다!

• 선형 모형을 편미분한 그레디언트 벡터의 결과는 가중치 벡터임
  
  
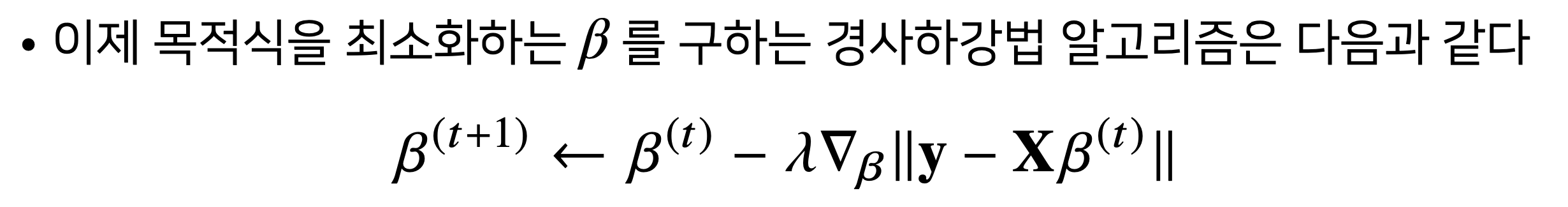  여기서 람다는 학습률을 의미함

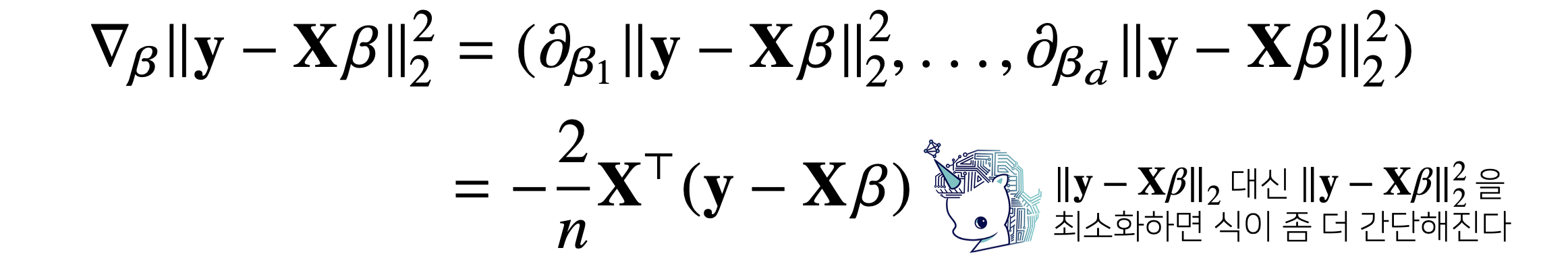
• 어차피 L2 Norm을 최소화하는 $\beta$를 찾나, L2 Norm의 제곱을 최소화하는 $\beta$를 찾나 둘 다 동일! 그런데 제곱을 활용하면 식이 더 간편해지니 이렇게 사용함

• 즉, grad = - transpose(x) @ error 꼴

확률적 경사하강법(SGD)

• 비선형회귀 문제의 경우, 목적식이 볼록하지 않을(non-convex) 수 있으므로 수렴이 항상 보장되지 않음
  => 변형된 경사하강법 필요!

• 확률적 경사하강법(Stochastic Gradient Descent, SGD)는 모든 데이터를 활용하여 업데이트하는 대신, 일부 데이터(mini-batch)만을 활용하여 업데이트 수행

  • 단점(?): 매번 다른 미니배치를 사용하여 곡선모양이 매번 바뀜 (그래도 방향은 얼추 비슷하게 감)
  • 장점: 미니배치를 활용하기 때문에 연산자원을 효율적으로 활용 가능 (연산량 $b/n$으로 감소)
    

• 결론적으로, 딥러닝의 경우 SGD가 경사하강법보다 주로 더 나은 성능을 보임

• 기존의 learning rate, 학습 횟수에 더해 mini-batch size 도 중요한 hyper parameter임