SVD(Singular Vector Decomposition)

2. SVD

정의

• SVD(Singular Value Decomposition) - 특이값 분해

• A : 실제 데이터
• U : left singular matrix(특이행렬), orthogonal matrix(직교행렬)
• V : left singular matrix(특이행렬), orthogonal matrix(직교행렬)
• $\sum$ : singular values(특이값), 대각행렬(대각선에 위치한 elements는 내림차순으로 정렬)
• 용어 정리
  • 특이행렬 : 역행렬이 존재하지 않는 행렬
  • 직교행렬 : $AA^\mathsf{T} = I$ 인 A를 지칭함

의미 파악

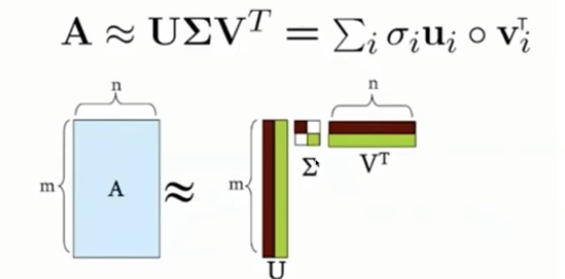
• A라는 input matrix는 다음과 같이 분해하여 A와 비슷한 근사행렬을 만들 수 있다

• 즉, 여기서 우리는 $\sum$의 크기(r r)인 r을 줄여서 차원 감소시켜 정보를 압축*할 수 있다는 의미

• A를 $U\sum{V^T}$꼴로 근사되기 때문에 우리는 A에서 압축된 행렬 $U$를 사용하기로 함

• 지금부터 r은 문서들의 concept라고 생각

  • r은 latent variable로 이해(의미를 가지고는 있지만, 눈에는 보이지 않는다는 개념)

    

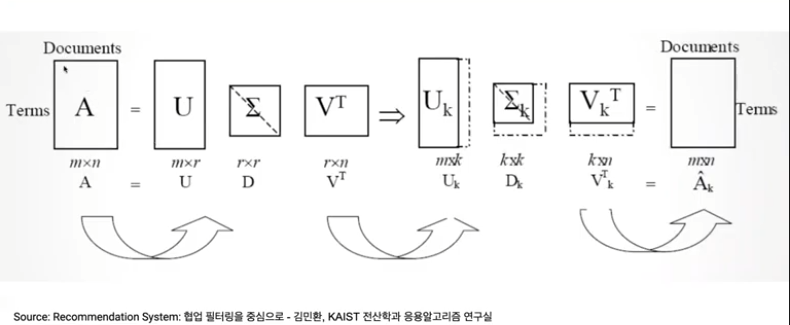
  • $\sum$은 대각행렬이고, 각 element들은 큰 순서대로 내림차순으로 정렬되었기 때문에, 이것을 풀이하자면 좌측 하단으로 갈수록 상대적으로 중요하지 않은 값들이 저장된다는 의미이다

  • 날려버린다 하더라도, A의 형태(m * n)은 유지된다!!! ⇒ 형태는 유지, 정보량은 줄어듦

예시

• 영화 추천 시스템

  

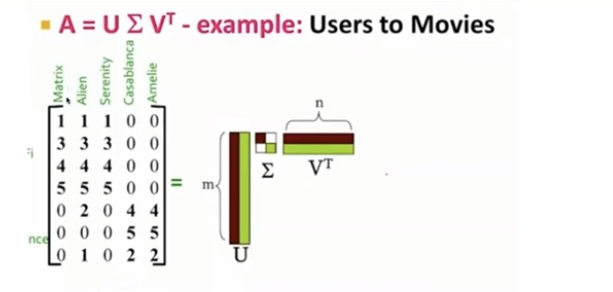
  • 행은 user, 열은 movie를 의미(즉, 각 user들이 본 영화에 대해 평점을 매겼다는 것을 행렬로 표현)

    

  • U는 각각의 user와 영화의 concept을 mapping한 행렬

    • 여기서 U를 보면, user1의 경우(U의 첫번째 행), SciFi계열 영화 주로 봄
    • 영화의 concept을 정해둔 건 아닌데, latent factor가 사후적으로 결정되었음

  • $\sum$ : SF영화가 영화를 추천하는데 많은 영향을 준다는 것(1행 1열)을 알 수 있음

  • V : 각각의 영화가 어떤 concept와 mapping되는지

    • V의 1행 1열을 통해 matrix는 SF성향 영화라는 것을 알 수 있음

• 이미지 압축

  

  • 다음 사진은 $\sum$의 r을 줄이면서 이미지를 압축시키는 것을 보여줌
  • 이미지를 압축하면서 화질을 깨지는 이유는 중요한 정보를 위주로 담기 때문에 나머지 정보를 버리면서 깨지는 현상 발생

수식

• 각각의 행렬은 그럼 어떻게 구해지느냐?
• R을 기준으로
• U : $AA^T$ 의 고유벡터(eigenvector)
• V : $A^TA$ 의 고유벡터(eigenvector)
• $\sum$ : the square roots of the non-zero eigenvalues of the $AA^T$ and $A^TA$ matrices.

참고 사이트

1. SVD
   • 강의 영상 : https://www.youtube.com/watch?v=VUUIrbMKUT4
   • SVD in R : https://rpubs.com/aaronsc32/singular-value-decomposition-r
   • 고유값, 고유벡터 : https://rfriend.tistory.com/181