Hash Function

🌩️ Hash Function(해시함수)

Hash Function - 임의의 길이를 가진 데이터를 입력받아 고정된 길이의 값(Hash Value)을 출력하는 함수

⚡️해시함수의 특징

• 단방향성
  • 입력 데이터 -> 해시값은 쉽지만, 입력데이터를 찾아내는 역변환은 불가능하다. 이는 데이터의 무결성을 보장할 수 있다.
  • 역상 저항성(preimage resistance)를 통해 단방향성을 평가할 수 있다.
  • 역상 저항성이 높으면 해시함수가 특정한 값을 출력하는 입력값을 찾기 어려움

• 해시 충돌(Hash Collision)
  • 서로 다른 입력값에 대하여 같은 해시값을 생성할 수 있음
  • 충돌 저항성(preimage resistance)을 통해 해시 충돌을 평가

• 입력값이 아주 일부분만 변경되어도 전혀 다른 결과값을 가짐

• 고정된 결과값의 길이
  • 해시함수는 항상 일정 길이의 결과값을 출력 ⇒ 데이터의 일관성과 효율적인 처리에 용이하다.
  • 해시값을 통해 데이터의 무결성을 검사 할 수 있다.

---

⚡️해시함수의 안전성을 평가하는 요소

• 역상 저항성(preimage resistance)
  • $y$가 주어지고, $f(x) = y$ 인 $x$를 찾는 것이 어려움
  • 제 1 역상 공격($x$를 찾는 것)에 대해 안전함
  • 출력이 n-bit일 경우 역상 저항성의 강도도 n과 동일
    
    
• 제 2 역상 저항성
  • $f(x)=y$인 $x, y$가 주어지고, $f(x’)=y$인 $x’$를 찾는 것이 어려움
  • 제 2 역상 공격($x’$를 찾는 것)에 대해 안전함
  • 출력이 n-bit일 경우 역상 저항성의 강도도 n과 동일하거나 약간 짧음
    
    
• 충돌 저항성
  • $f(x) = f(x’)$인 $x, x’$를 찾는 것이 어려움
  • 출력이 n-bit일 경우 충돌 저항성의 강도는 n의 절반정도임(Birthday Problem)
  
  

⚡️Birthday Problem

• 비둘기집 원리 - n개 보다 많은 물건을 n개의 바구니에 담을 경우 어느 한 바구니에는 반드시 2개 이상의 물건이 담김 ⇒ 1년은 365일 이므로 366명이 모이게 되면 생일이 같은 사람이 있을 확률은 1이다.

• 한 집단에 23명만 모여도 생일이 같은 사람이 있을 확률은 50%를 넘어간다.

  • 생일이 같을 확률 = 1 - 생일이 같지 않을 확률
  • A와 B(서로 다른 2명)의 생일이 같지않을 확률
  • 23명 중 생일이 같은 사람이 있을 확률 = 1 - 23명 모두 생일이 같지않을 확률
    p의 실제값은 0.5073이다
    
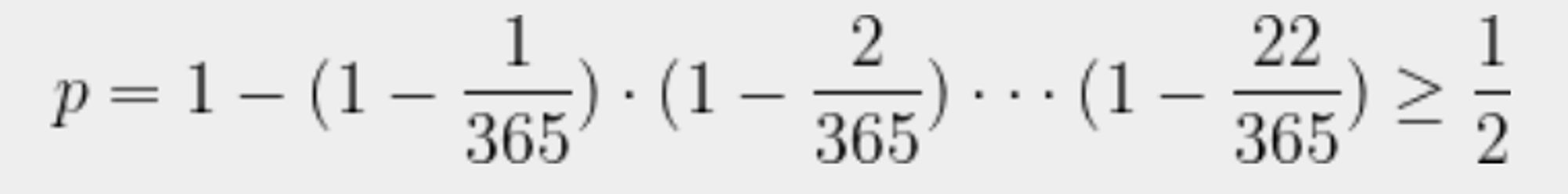
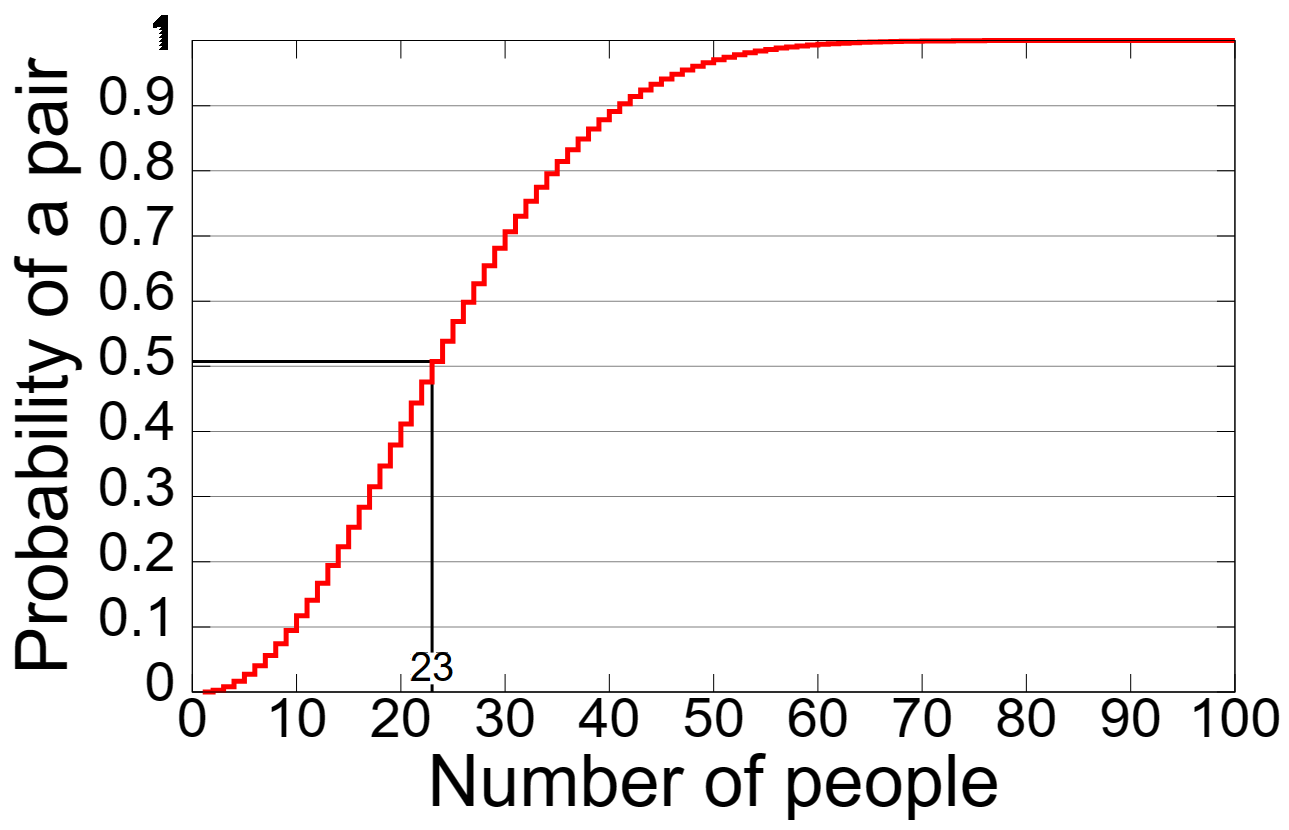
  • 사람 수가 늘어나면 확률도 급격히 늘어난다
    
  
  

• q개의 랜덤 입력값에 대해 해시 충돌이 일어날 확률(n-bit 출력의 해시함수)
  

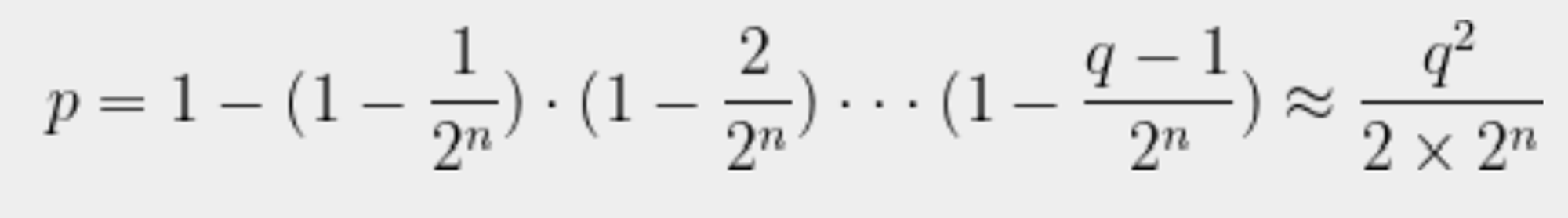
• 해시충돌 쌍을 찾을 확률을 0.5이상으로 갖기위한 해시값의 개수
  아래 식을 통해 해시함수의 안전성은 출력비트 n의 절반 수준임을 알 수 있다.
  

---

⚡️해시함수 in 블록체인

비트코인에서는 SHA-256을 해시 생성 및 보안에 사용한다.

블록체인 데이터를 고유한 해시값으로 변환하여 저장함으로써 식별성, 데이터의 무결성등의 장점을 얻을 수 있다

• Transaction Hash(=Transaction ID = TXID)
  • TXID는 거래내역의 식별자이다.
  • 트랜잭션을 해시함수를 거쳐 일정한 길이의 해시값으로 변환한다.
  • 식별이 용이하고, 무결성 확인이 가능하다.

❓Transaction은 거래 전표로써 수신, 발신 주소, 금액, 수수료 등을 표시한 거래 내역이다.

• Block Hash

  • 블록은 블록 헤더 정보에 기반한 블록 고유의 해시값을 가진다.
  • 블록의 식별자

• Merkle Root(=Root Hash)

  • Merkle Tree - 여러 데이터에 의해 단계적으로 해시 함수를 적용하여 하나의 해시값으로 나타내는 데이터 구조이다. ⇒ 여러개의 데이터를 하나의 해시값으로 만든다.
    
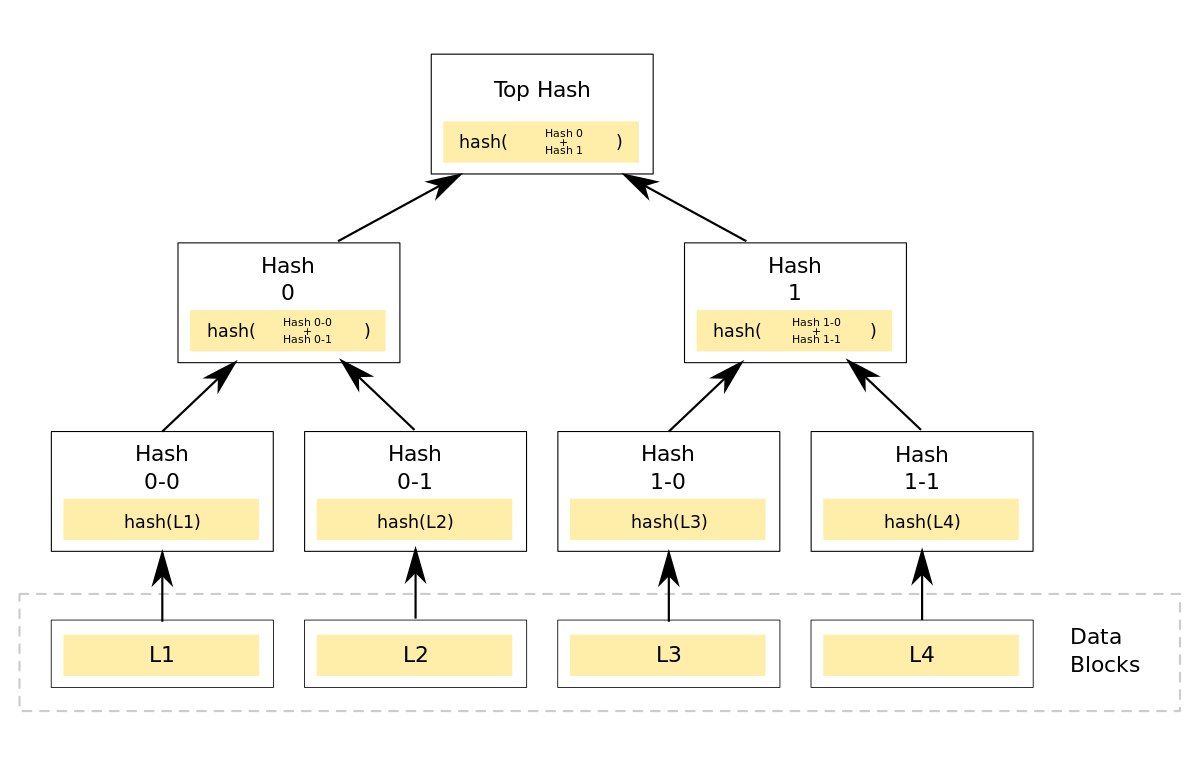
  • 무결성 검사에 용이하다. 하위 해시값이 바뀌면 루트해시(최상위 해시)값도 바뀌므로 루트해시만 비교해보아도 데이터의 무결성을 검사할 수 있다.
  
  

• SHA-256

  • 무결성 검증에 이용되는 암호화 해싱 알고리즘
  • 입력 문자열을 256-bit길이의 키로 변환한다.
    

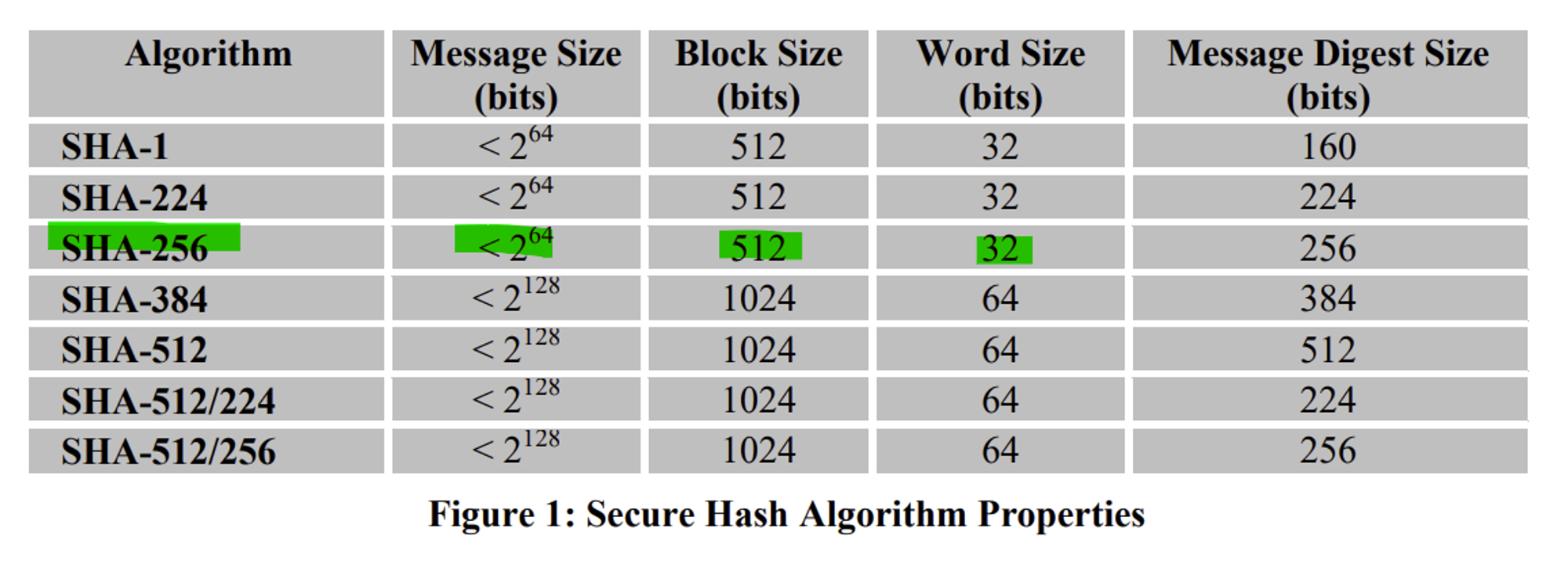
참조
https://m.blog.naver.com/alwaysneoi/220261751961
https://www.codestates.com/blog/content/%EB%B8%94%EB%A1%9D%EC%B2%B4%EC%9D%B8-%ED%95%B4%EC%8B%9C%ED%95%A8%EC%88%98
https://jusths.tistory.com/43
https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf