맥스 풀링의 원리

맥스 풀링은 단순하다. (6,6) 사이즈의 이미지가 있다고 할 때, 그 절반인 (3,3) 크기의 사이즈로 이미지를 줄이는 것에 불과하다.
가장 큰 수를 유지하면서 사이즈를 줄이는 방식을 max pooling이라고 부른다.
맥스 풀링 방식을 쓰는 이유는 풀링의 대상이 컨볼루션의 결과 특징 맵이기 때문이다.
큰 값으로 표현된 부분은 컨볼루션 필터로 찾으려 했던 특징이 나타난 것을 의미한다. 맥스 풀링은 유의미한 정보를 남기면서 사이즈를 줄이려는 의도가 담겨있다.
CNN의 구조는 컨볼루션 레이어, 풀링 레이어, 플래튼 레이어로 3개의 조합으로 이루어져 있다.

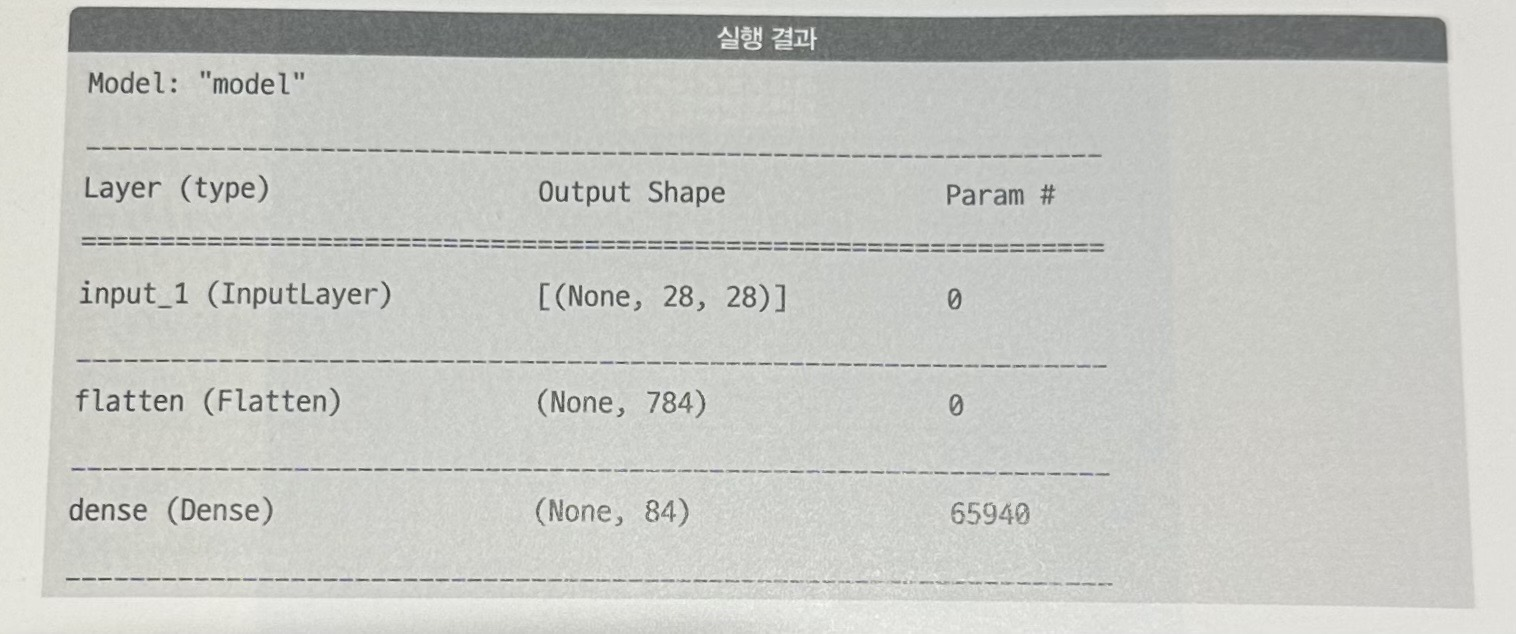
플래튼만 사용한 모델

플랠튼 레이어에서는 (28,28)의 2차원 형태의 숫자들을 한 줄로 펼쳐서 784개의 변수를 가지는 데이터를 출력한다.
첫번째 히든레이어(dense)는 84개의 칼럼을 가지는 데이터를 출력하고, 마지막 레이어(dense_1)에서는 10개의 칼럼을 가지는 출력을 만든다.
첫번째 히든 레이어에서 84개 칼럼의 출력을 만든다는 것은 84개의 출력이 있다는 말인데, 하나의 수식을 위해서 784개의 가중치와 1개의 바이어스가 필요하므로 이 히든 레이어를 구성하는 데 필요한 가중치의 수는 84x(784+1) = 65,940개이다.
마지막 레이어는 10개의 수식이 있고, 하나의 수식을 위해서는 84개의 가중치와 1개의 바이어스가 필요하므로 마지막 출력층을 구성하는 데 필요한 가중치의 수는 10x(84+1)=850개이다.

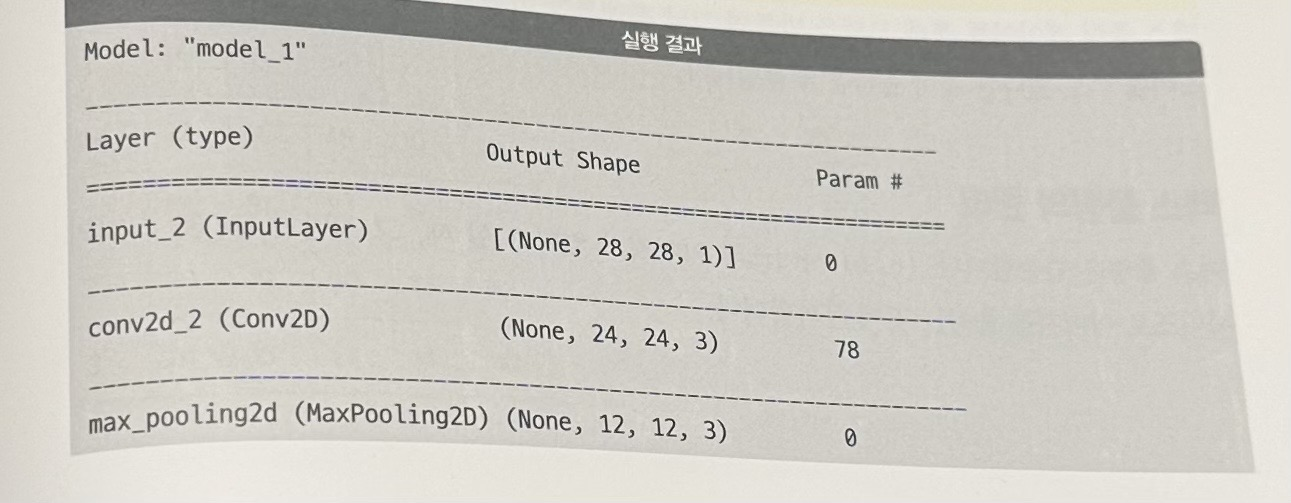
컨볼루션 레이어를 추가한 모델

flatten 레이어의 입력으로 (20,20,6)의 형태로 입력을 받는다. (20,20) 이미지가 6장 있다는 말이다. 한장에 400개의 숫자가 있을 것이고 거기에 6을 곱하여 2400개 칼럼에 데이터를 출력한다.
다음 히든레이어(dense)에서 84개 칼럼의 출력을 만드는데, 이는 84개의 수식이 있다는 말이고, 이 하나의 수식을 위해서는 2400개의 가중치와 1개의 바이어스가 필요하므로 히든 레이어를 구성하는 데 필요한 가중치의 수는 84x(2400+1) =201,684개이다.

컨볼루션 레이어(conv2d_1)로 출력된 특징 맵의 개수가 증가하면 플래튼 이후 입력으로 사용할 데이터의 칼럼 수가 증가하고, 이는 곧 컴퓨터가 찾아야하는 가중치 수의 증가를 의미한다.

풀링 레이어를 사용한 모델

플래튼 레이어(flatten_1)에서는 입력으로 (4,4) 이미지 6장을 사용하는데, 한장에 16개의 숫자가 있을 것이고 16x6=96개의 칼럼에 데이터를 출력한다.
다음 히든 레이어(dense_2)에서는 84개의 칼럼에 출력을 만드는데, 그것은 84개의 수식이 있다는 얘기이다. 하나의 수식을 위해서는 그 16개의 가중치와 1개의 바이어스가 필요하므로 하든 레이어를 구성하는데 필요한 가중치 수는 84x(96+1) = 8,148개이다.
컨볼루션 레이어로 출력된 특징맵 이미지의 사이즈가 맥스 풀링 레이어를 거치면서 절반으로 줄어드는 것을 확인할 수 있따.
맥스 풀링 레이어를 통해 모델을 만들면 그냥 플래튼만 이용해 만든 모델보다도 가중치 수가 적어질 수도 있다.