[자료구조] 트리?? 그게 뭔데? 🌳

chiyongs·2022년 6월 22일

트리의 개념 🌳

트리 구조란 정보의 항목들이 가지로 연결될 수 있게 데이터가 조직되는 것을 말합니다. 또한, 그래프의 일종으로, 여러 노드가 한 노드를 가리킬 수 없는 구조입니다. 간단하게는 회로가 없고, 서로 다른 두 노드를 잇는 길이 하나뿐인 그래프를 트리라고 부릅니다. 계층적인 자료를 표현하는 데 이용되는 자료구조이며 노드로 이루어져 있습니다.

ex) 혈통표, 계보표

정의

트리는 1개 이상의 노드로 이루어진 유한 집합

노드 중에는 루트라는 노드가 하나 있고,
나머지 노드들은 n개의 분리 집합으로 분할될 수 있습니다. 각각의 분리 집합은 하나의 트리이며 루트의 서브트리라고 합니다.

용어

노드(node) : 한 정보 아이템에 다른 노드로 뻗어진 가지를 합친 것
차수(degree) : 한 노드의 서브트리의 수 = 각 노드가 지닌 가지의 수 = 각 노드가 가진 자식 노드의 수
리프(leaf) or 단말노드(terminal node) : 차수가 0인 노드 == 서브트리가 없는 노드
비단말 노드(non-terminal node) : 차수가 0이 아닌 노드 == 서브트리가 있는 노드
조상(ancestors) : 루트에서부터 그 노드에 이르는 경로상에 있는 모든 노드들
간선(edge) : 노드를 연결하는 선, branch or link
노드의 크기(size) : 자신을 포함한 모든 자손 노드의 개수
노드의 깊이(depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
노드의 레벨(level) : 트리의 특정 깊이를 가지는 노드의 집합
형제(sibling) : 같은 부모를 가지는 노드
트리의 차수(degree of a tree) : 그 트리에 있는 노드의 최대 차수
트리의 높이 (height) : 루트 노드에서 가장 깊숙히 있는 노드까지의 깊이

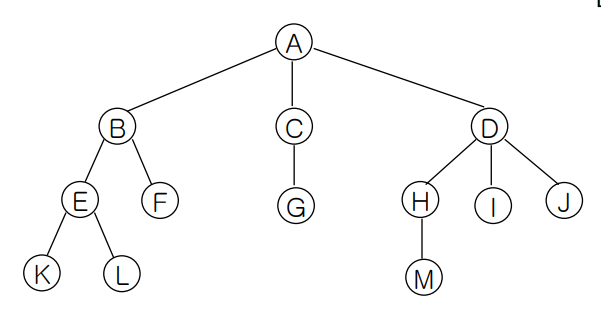
위 트리를 리스트로 표현한다면

(A(B(E(K,L)F),C(G),D(H(M),I,J)))

트리의 특징

노드로 이루어진 자료구조이다.
1개의 루트 노드를 가진다.
계층 모델이다. 디렉토리 구조 생각
루트 노드는 0개 이상의 자식 노드를 가지고 있다.
노드가 N개인 트리는 항상 N-1개의 간선을 가진다.
루트에서 어떤 노드로 가는 경로는 항상 unique하다. → 두 개의 정점 사이에 반드시 1개의 경로만 가진다.
비선형 자료구조이다.

💡 선형 자료구조는 자료를 저장하고 꺼내는 것에 초점을 맞추고 비선형 자료구조는 표현에 초점이 맞춰져 있습니다.

이진트리 Binary Tree

정의

이진트리는 공백이거나 루트와 왼쪽 서브트리, 오른쪽 서브트리라고 하는 2개의 분리된 이진트리로 구성된 노드의 유한 집합

특성

• 한 노드의 차수가 2보다 크지 않다. == 한 노드는 최대 두 개의 자식 노드를 가진다.

• 0개의 노드를 가질 수 있다. → 일반 트리에서는 0개의 노드를 가진 트리는 없으나 공백 이진 트리는 존재

• 자식의 순서를 구분한다. == 왼쪽 서브트리와 오른쪽 서브트리를 구별해야 한다.

성질

레벨 i에서의 최대 노드 수 : $2^{i-1}$ (i≥1)
깊이가 k인 이진 트리의 최대 노드 수 : $2^k-1 (k>=1)$
리프 노드 수 = 차수가 2인 노드 수 + 1
포화 이진 트리
- 깊이가 k이고, 노드 수가 2^k -1 (k≥0)인 이진 트리

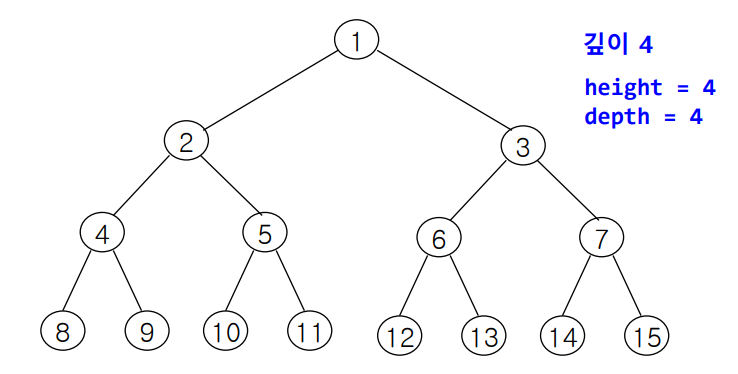
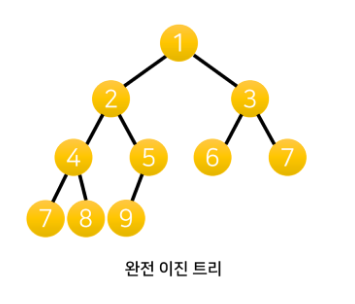
완전 이진 트리
- 깊이가 k이고 노드 수가 n인 이진 트리
- 각 노드들이 깊이가 k인 포화 이진 트리에서 1부터 n까지 번호를 붙인 노드와 1대 1로 일치
- n개의 노드를 가진 완전 이진 트리의 높이 : $log_2(n+1)$

순회

순회 방법 : LVR, LRV, VLR, VRL, RVL, RLV

L : 왼쪽 이동, V : 노드방문, R : 오른쪽 이동
왼쪽을 오른쪽보다 먼저 방문(LR)
- LVR : 중위 순회 (inorder traversal)
- VLR : 전위 순회 (preorder traversal)
- LRV : 후위 순회 (postorder traversal)

이진 탐색 트리(Binary Search Tree = BST)

정의

이진 탐색 트리는 공백이 가능하고, 만약 공백이 아니라면
1. 모든 원소는 서로 상이한 키를 갖는다.
2. 왼쪽 서브트리의 키들은 구 루트의 키보다 작다.
3. 오른쪽 서브트리의 키들은 그 루트의 키보다 크다.
4. 왼쪽과 오른쪽 서브트리도 이원 탐색 트리다.

출처 : https://blog.penjee.com/5-gifs-to-understand-binary-search-tree/#binary-search-tree-insertion-node

BST의 시간복잡도

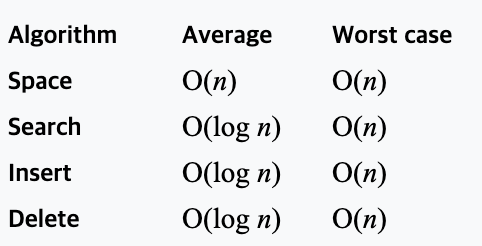
이진탐색트리에서의 삽입, 삭제, 탐색 연산의 시간복잡도는 트리의 높이에 비례한다. 따라서, 균형잡힌 BST에서는 O(logN)의 시간복잡도를 가지지만 트리가 편향되어있다면 최악의 경우 O(N)의 시간복잡도를 가질 수 있다.

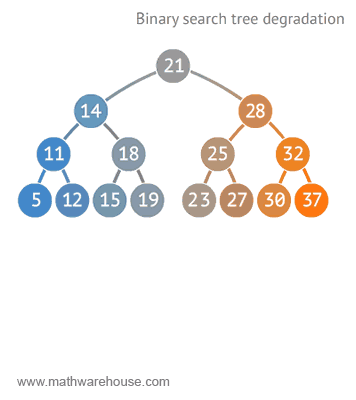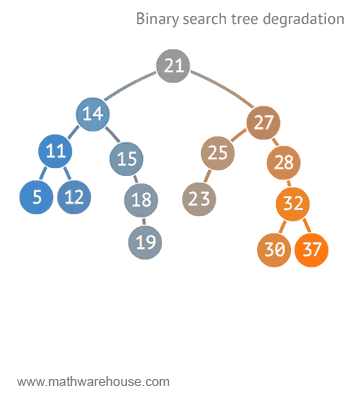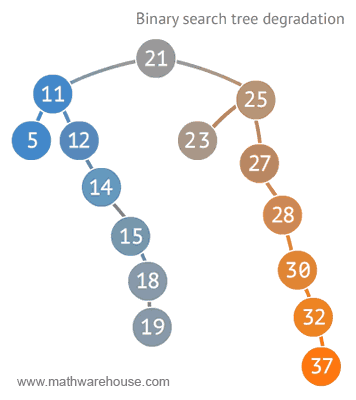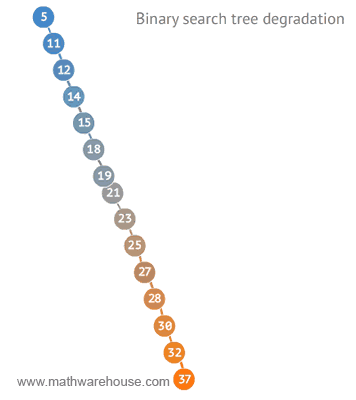
이러한 이진탐색트리의 편향문제를 해결하기 위해 AVL Tree, Red-Black Tree 등의 자료구조가 등장한다.

출처 : https://blog.penjee.com/5-gifs-to-understand-binary-search-tree/#binary-search-tree-insertion-node

BST의 탐색

k = 루트의 키 : 성공 → 종료
k < 루트의 키 : 왼쪽 서브트리 탐색
k > 루트의 키 : 오른쪽 서브트리 탐색

BST 구현

search (탐색)
insert (삽입)
delete (삭제)

탐색

현재 노드의 값과 찾고자 하는 값이 일치하면 현재 노드를 반환합니다.
현재 노드의 값보다 찾고자 하는 값이 크면 오른쪽 자식노드로 이동합니다.
현재 노드의 값보다 찾고자 하는 값이 작으면 왼쪽 자식노드로 이동합니다.
위 1~3 과정을 반복합니다.

	public Node search(int key) {
		Node temp = this.head;
		while (temp != null) {
			if (temp.key == key) {
				return temp;
			}
			temp = temp.key < key ? temp.right : temp.left;
		}
		return null;
	}

삽입

현재 노드가 null이면 현재 위치에 노드를 삽입합니다.
현재 노드의 값이 삽입할 값과 일치하면 삽입하지 않고 false를 반환합니다.
현재 노드의 값보다 삽입할 값이 크면 오른쪽 자식노드로 이동합니다.
현재 노드의 값보다 삽입할 값이 작으면 왼쪽 자식노드로 이동합니다.
위 1~4 과정을 반복합니다.

public boolean insert(Node input) {
		if (this.head == null) {
			this.head = input;
			return true;
		}
		Node temp = head;
		Node parent = temp.parent;

		while (temp != null) {
			if (input.key == temp.key)
				return false;
			temp = temp.key < input.key ? temp.right : temp.left;
			parent = temp;
		}

		if (parent.key < input.key)
			parent.right = input;
		else
			parent.left = input;

		input.parent = parent;
		return true;
	}

삭제

삭제할 값을 가진 노드를 탐색합니다.
삭제할 노드가 존재하지 않으면 false를 반환합니다.
삭제할 노드가 단말노드라면 삭제하고 true를 반환합니다.
한쪽 서브트리만 존재할 경우, 삭제할 노드의 자식노드와 부모노드를 연결하고 true를 반환합니다.
양쪽 서브트리가 모두 존재한다면, 삭제할 노드를 대체할 노드를 찾아 서브트리와 부모노드를 연결합니다.

public boolean delete(int key) {
		 Node target = search(key);
		 
		 if(target == null) {
			 // 삭제하려는 대상이 없음
			 return false;
		 }
		 if(target.left == null && target.right == null) {
			 // 단말 노드인 경우
			 target = null;
			 return true;
		 }
		 
		 // 오른쪽 서브트리만 존재할 때
		 if(target.left == null) {
			 if(target.parent.left == target) target.parent.left = target.right;
			 
			 if(target.parent.right == target) target.parent.right = target.right;
			 
			 target.right.parent = target.parent;
			 return true;
		 }
		 
		 // 왼쪽 서브트리만 존재할 때
		 if(target.right == null) {
			 if(target.parent.left == target) target.parent.left = target.left;
			 if(target.parent.right == target) target.parent.right = target.left;
			 
			 target.left.parent = target.parent;
		 } else {
			 // 양쪽 서브트리 모두 존재할 뗴
			 Node alternativeNode = findMinNode(target.right);
			 if(alternativeNode == target.right) target.right = null;
			 else alternativeNode.parent.left = null;
			 
			 alternativeNode.left = target.left;
			 if(alternativeNode.left != null) alternativeNode.left.parent = alternativeNode;

			 alternativeNode.right = target.right;
			 if(alternativeNode.right != null) alternativeNode.right.parent = alternativeNode;

			 alternativeNode.parent = target.parent;
			 
			 if(target.parent.left == target) target.parent.left = alternativeNode;
			 else if(target.parent.right == target) target.parent.right = alternativeNode;
			 target = null;
			 return true;
		 }
		 return false;
	}
	
	public Node findMinNode(Node target) {
		while(target.left != null) target = target.left;
		return target;
	}

BST 탐색, 삽입, 삭제 구현

package sample;

public class BST {

	private Node head;

	public class Node {
		Node left;
		Node right;
		int key;
		Node parent;
	}

	public Node search(int key) {
		Node temp = this.head;
		while (temp != null) {
			if (temp.key == key) {
				return temp;
			}
			temp = temp.key < key ? temp.right : temp.left;
		}
		return null;
	}

	public boolean insert(Node input) {
		if (this.head == null) {
			this.head = input;
			return true;
		}
		Node temp = head;
		Node parent = temp.parent;

		while (temp != null) {
			if (input.key == temp.key)
				return false;
			temp = temp.key < input.key ? temp.right : temp.left;
			parent = temp;
		}

		if (parent.key < input.key)
			parent.right = input;
		else
			parent.left = input;

		input.parent = parent;
		return true;
	}
	
	public boolean delete(int key) {
		 Node target = search(key);
		 
		 if(target == null) {
			 // 삭제하려는 대상이 없음
			 return false;
		 }
		 if(target.left == null && target.right == null) {
			 // 단말 노드인 경우
			 target = null;
			 return true;
		 }
		 
		 // 오른쪽 서브트리만 존재할 때
		 if(target.left == null) {
			 if(target.parent.left == target) target.parent.left = target.right;
			 
			 if(target.parent.right == target) target.parent.right = target.right;
			 
			 target.right.parent = target.parent;
			 return true;
		 }
		 
		 // 왼쪽 서브트리만 존재할 때
		 if(target.right == null) {
			 if(target.parent.left == target) target.parent.left = target.left;
			 if(target.parent.right == target) target.parent.right = target.left;
			 
			 target.left.parent = target.parent;
		 } else {
			 // 양쪽 서브트리 모두 존재할 뗴
			 Node alternativeNode = findMinNode(target.right);
			 if(alternativeNode == target.right) target.right = null;
			 else alternativeNode.parent.left = null;
			 
			 alternativeNode.left = target.left;
			 if(alternativeNode.left != null) alternativeNode.left.parent = alternativeNode;

			 alternativeNode.right = target.right;
			 if(alternativeNode.right != null) alternativeNode.right.parent = alternativeNode;

			 alternativeNode.parent = target.parent;
			 
			 if(target.parent.left == target) target.parent.left = alternativeNode;
			 else if(target.parent.right == target) target.parent.right = alternativeNode;
			 target = null;
			 return true;
		 }
		 return false;
	}
	
	public Node findMinNode(Node target) {
		while(target.left != null) target = target.left;
		return target;
	}

	public static void main(String[] args) {

	}

}

트리 자료구조에 대해 공부하며 기록한 글이어서 잘못된 내용이 있다면 댓글로 알려주시면 감사하겠습니다!! 😊

chiyongs

이전 포스트

객체지향 프로그래밍?? 그게 뭔데?

다음 포스트