1.1 과목 소개

1.2 강의소개 및 계획소개

Definition of Computer Science

Computer science is science of intelligence.

Application of Computer Science

Extension of Human Intelligence, Human Instince, Human Reality

이 수업은 크게 네 가지 파트로 나눠져 있다.

1. 컴퓨터의 원천 아이디어
2. 컴퓨터의 구현
3. 컴퓨터의 활용 : SW
4. 컴퓨터를 통한 확장

1.3 컴퓨터의 탄생비화1 - 수리명제 자동판결 문제

컴퓨터라는 도구의 놀라운 특이점

컴퓨터는 다른 도구와 다르다.

다른 도구들은 어떤 하나의 문제점만을 해결하기 위한 도구이다.

그러나 컴퓨터는 만능이다. 이것이 바로 컴퓨터라는 도구의 놀라운 특이점이다.

“보편만능의 도구(universal machine)”

컴퓨터 디자인의 “탄생 비화”

20세기 수학의 좌절을 재확인하는 데 동원된 소품

(아래서 더 자세하게 상술)

수학자들의 꿈

David Hilbert라는 수학자는 다음과 같은 생각을 한다.

논리적 추론을 할 때 패턴이 존재하는데 이것의 개수가 많지 않다. 즉, 유한 개의 유형으로 정리할 수 있다.

추론 규칙의 예를 들면 다음과 같다.

$A \rightarrow B = \frac{A}{B} =$ “A이면 B다”

$A \bigwedge B \rightarrow C = \frac{A \space B}{C} =$ “A 그리고 B이면 C이다.”

$\frac{A \space \space B}{A \bigwedge B}$.... 등등

이런 식으로 추론 규칙이 몇 가지 없을 것다고 생각한 것이다.

그렇다면 위와 같이 몇 가지의 추론 규칙을 정하고 이를 활용하면 모든 수학 문제들을 위와 추론 규칙들을 이용해서 풀어낼 수 있다고 생각한다.

그래서 직접 위와 같은 아이디어를 이용해서 문제를 풀어보고자 수학자들에게 이런 문제를 소개한다. 그리고 이 문제를 수리 명제 자동 판결 문제(Decision Problem)이라고 한다.

💡 참고로 → 에 해당하는 논리식은 위와 같이 분수꼴로 표현할 수 있다.

수리 명제 자동 판결 문제(Decision Problem), Entscheidungsproblem

모든 명제들의 참/거짓을 “기계적으로” 판명할 수 없을까?

참인 모든 명제들을 “기계적으로” 만들어낼 수 없을까?

자동 판결 문제는 유한 개의 추론 규칙을 찾아낸 후에, 이 추론 규칙을 이용하여 자동으로 수리 명제들을 판결할 수 있는가?에 대한 문제이다.

그런데 이 문제는 위의 언급한 내용대로 해석할 수도 있다. 왜냐하면 추론 규칙의 전제에 해당하는 부분만 진실로 증명하면 나머지는 알아서 추론 규칙에 의해서 결론들이 도출되기 때문이다.

이때 당시에 수학자들은 이 문제를 풀기 위해서 나선다.

“기계적”

기계적이라고 하면 “아무 생각 없이 자동으로 술술”이 핵심이다.

즉, 수리 명제를 판단하는 알고리즘을 찾는다면, 이 알고리즘대로 수행할 수 있는 기계를 만들 수 있다. 그렇다면 ‘자동으로 술술’ 문제들을 해결해나갈 수 있다.

그런데 이때 이 기계는 모든 수리 명제를 생성해낼 수 있어야 한다. 즉, 어떤 알고리즘을 넣어두면 자동으로 더 필요한 규칙들을 알아서 생성해낼 수도 있어야 한다. 다시 말해 계속해서 이전에 알아냈던 규칙들이 연쇄 작용을 거쳐서 새로운 규칙들도 생성되는 방식인 것이다.

추론 기계 : 추론 규칙

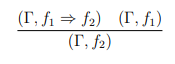
예를 들어서 $f_1 \Rightarrow f_2, \space f_1$이 참임을 밝혀졌다면, $f_2$가 자동으로 참임이 증명되는 것이다. 그렇게 되면, 다시 $f_2$를 이용하여 새로운 규칙을 생성해낼 수 있게 된다. 바로 아래와 같이 말이다.

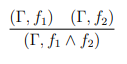
이처럼 계속해서 추론이 이어지게 만들 수 있는 원자격에 해당하는 추론 규칙들만 알아낼 수 있다면, 계속해서 새로운 추론 규칙을 만들어 낼 수 있게 된다. 그렇게 이 세상에 존재하는 모든 추론 규칙들을 만들어낸다면, 그 규칙을 이용하여 이 세상 모든 수학 문제들을 풀어낼 수 있게 된다.

다시 정리해본다. 즉, 원소격에 해당하는 몇 가지 추론 규칙을 알아낼 수 있다면, 그 추론 규칙들을 조합하여 새로운 추론 규칙을 추가할 수 있다. 이를 재귀적으로 활용하여 계속해서 새로운 추론 규칙 또한 만들어낼 수 있다. 그럼 결론적으로는 이 세상 모든 수리 명제들을 알아낼 수 있다는게 아이디어다. 만약 이 세상 모든 참인 수리 명제들을 알아냈다면, 우리가 어떤 문제를 만나든 그 문제에 대응되는 참인 수리 명제를 활용하여 그 문제를 풀어낼 수 있게 된다는 것이다.

1931년, 수학계의 “좌절” 혹은 “희소식”

“기계적인 방식만으론 사실인지 판정할 수 없는, 그런 명제가 존재한다.”

위의 명제가 참임을 쿠르트 괴델이 증명해낸다.

즉, 힐베르트의 꿈은 쿠르트 괴델이란 수학자에 의해 깨지게 된다.

원소격에 해당하는 몇 가지 추론 규칙들을 기계적으로 이미 알려진 방식대로 조합하면, 새로운 추론규칙을 만들어 낼 수 있다.

이때 힐베르트는 이 방법을 계속해서 재귀적으로 적용하면 이 세상 모든 수리 명제들을 만들어낼 수 있을 수 있겠다고 생각한다.

그러나 이런 생각은 괴델이 깨트린다. 괴델은 아무리 힐베르트가 말한 방식대로 수리 명제들을 조합한다고 해도, 절대로 참임을 판정해낼 수 없는 명제가 존재함을 증명해낸다.

1936년, 8월 9일 vs 5월 28일

앨런 튜링도 힐베르트가 제시한 문제에 대해서 듣게 된다. 그리고 또한 괴델의 증명도 알게 된다.

앨런 튜링은 괴델의 증명을 자신의 방식대로 다시 재증명하여 이를 논문으로 발표한다.

“계산 가능한 수에 대해서, 수리 명제 자동 판별 문제에 응용하면서”(On Computabel Numbers, with an Application to the Entscheidungsproblem)

튜링의 그 때 그 시절

떠나자 : 오리지날 논문 속으로

“기계적인 방식만으론 사실인지 판정할 수 없는, 그런 명제가 존재한다.”

앨런 튜링은 논문에서 먼저 기계적인 계산이란 뭔지 정의한다.

“1. Computing Machines”, “2. Definitions”

(이미지 : Part 1 강의자료 17쪽 참고)

튜링은 먼저 위와 같은 방식대로 어떤 기계를 정의한다. 그리고 이 기계를 통해서 계산할 수 있는 것만 기계적인 계산이라고 부르기로 정의한다.

이때 튜링이 정의한 기계를 튜링 머신이라고 부른다.

튜링 머신은 수학 문제들을 풀 수 있다.

그리고 중요한 점은 튜링 머신에 어떤 튜링 머신을 입력값으로 넣으면, 튜링 머신은 입력된 튜링 머신을 그대로 따라할 수 있다.(내장 프로그래밍 방식)

튜링 머신의 구성

1. 빈칸이 무한히 많은 테이프
2. 유한 개의 기호
3. 규칙표
4. 테이프를 읽고, 기호를 쓰고, 상태를 나타내는 기계

---

튜링 기계는 튜링이 구성한 수학적인 기계다. 그것은 추상적인 계산 기계다. 튜링은 인간이 실제로 어떻게 계산을 수행하는지를 관찰한 뒤, 계산의 본질적 요소를 추출하여 재구성함으로써 튜링 기계를 구성해냈다. 요컨대 튜링 기계는 인간이 계산하는 과정을 본떠서 만든 것이다.
[from “앨런 튜링과 현대 컴퓨터의 기원”]

튜링 기계가 나오게 된 아이디어나 마찬가지이다. 즉, 튜링 머신은 인간이 사고과정하는 과정을 모방하여 만들어진 것이라고도 할 수 있다.

참고자료

1. https://www.youtube.com/playlist?list=PL0Nf1KJu6Ui7yoc9RQ2TiiYL9Z0MKoggH
2. http://kwangkeunyi.snu.ac.kr/046.016/19/

위 글은 이광근 교수님의 유튜브 강의와 공개된 강의자료를 참고했음을 밝힙니다. 추후에 문제가 될 시 곧바로 삭제하겠습니다.