1. 유전자 분석을 통한 암 진단
1.1 프로젝트 소개
유전자 분석을 통해 암을 진단하는 인공지능을 만들어 본다.
1.2 데이터 살펴보기
실제 암 환자로부터 채취된 조직을 갈아서 유전자를 분석한 데이터
BRCA는 유방암, COAD는 대장암, LUAD는 폐암, THCA는 갑상선암
총 2,905명의 환자로부터 수집된 데이터
환자 한 명당 피쳐(유전자)수는 2만 개
데이터는 0부터 1 사이 숫자로 노멀라이즈
트레이닝:테스트 = 8:2
1.3 어떤 인공지능을 만드나
(1) 신경망의 구조
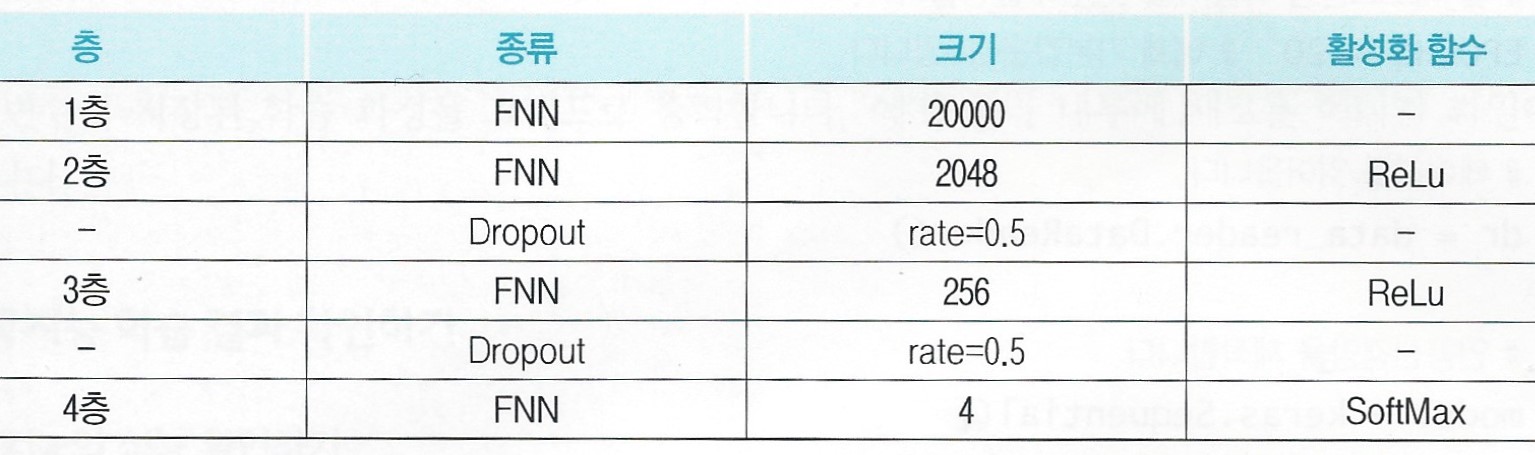
4층짜리 FNN
입력 데이터의 크기가 굉장히 크기에 입력층의 사이즈도 함께 커졌다.
2, 3층은 드롭아웃 적용
4층은 4개의 암 카테고리를 구분하기 위해 사이즈는 4
분류 문제이기에 활성화 함수는 softmax 함수
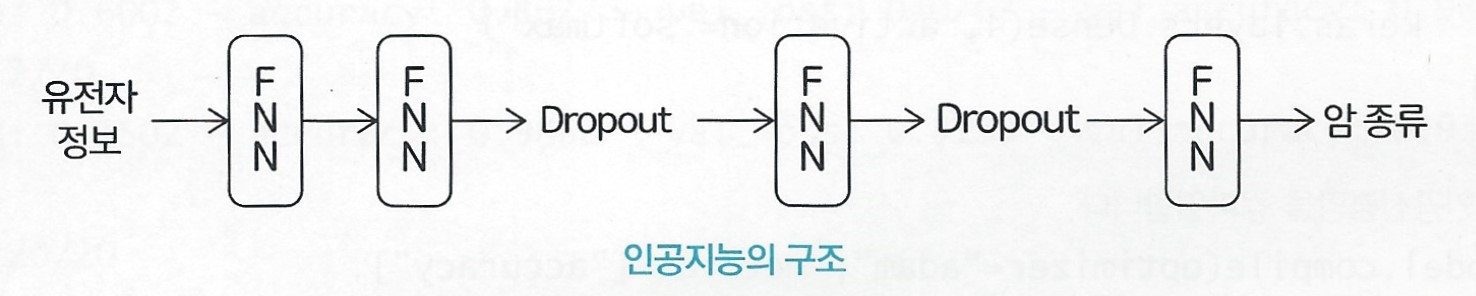
1.4 딥러닝 모델 코딩
from tensorflow import keras
import data_reader
# 몇 에포크 만큼 학습을 시킬 것인지 결정합니다.
EPOCHS = 20 # 예제 기본값은 20입니다.
# 데이터를 읽어옵니다.
dr = data_reader.DataReader()
# 인공신경망을 제작합니다.
model = keras.Sequential([
keras.layers.Dense(20000),
keras.layers.Dense(2048, activation="relu"),
keras.layers.Dropout(rate=0.5),
keras.layers.Dense(256, activation="relu"),
keras.layers.Dropout(rate=0.5),
keras.layers.Dense(4, activation='softmax')
])
# 인공신경망을 컴파일합니다.
model.compile(optimizer="adam", metrics=["accuracy"],
loss="sparse_categorical_crossentropy")loss는 "sparse_categorical_crossentropy"를 활용했다.
1.5 인공지능 학습
(1) 인공신경망 학습
# 인공신경망을 학습시킵니다.
print("************ TRAINING START ************ ")
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
history = model.fit(dr.train_X, dr.train_Y, epochs=EPOCHS,
validation_data=(dr.test_X, dr.test_Y),
callbacks=[early_stop])val_loss를 대상으로 콜백
fit() 함수로 학습 진행
(2) 학습 결과 출력
# 학습 결과를 그래프로 출력합니다.
data_reader.draw_graph(history)(3) 전체 코드
from tensorflow import keras
import data_reader
# 몇 에포크 만큼 학습을 시킬 것인지 결정합니다.
EPOCHS = 20 # 예제 기본값은 20입니다.
# 데이터를 읽어옵니다.
dr = data_reader.DataReader()
# 인공신경망을 제작합니다.
model = keras.Sequential([
keras.layers.Dense(20000),
keras.layers.Dense(2048, activation="relu"),
keras.layers.Dropout(rate=0.5),
keras.layers.Dense(256, activation="relu"),
keras.layers.Dropout(rate=0.5),
keras.layers.Dense(4, activation='softmax')
])
# 인공신경망을 컴파일합니다.
model.compile(optimizer="adam", metrics=["accuracy"],
loss="sparse_categorical_crossentropy")
# 인공신경망을 학습시킵니다.
print("************ TRAINING START ************ ")
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
history = model.fit(dr.train_X, dr.train_Y, epochs=EPOCHS,
validation_data=(dr.test_X, dr.test_Y),
callbacks=[early_stop])
# 학습 결과를 그래프로 출력합니다.
data_reader.draw_graph(history)1.6 인공지능 학습 결과 확인하기
(1) 인공지능 성능 확인하기
가장 우측의 val_accuracy가 최종 성능
정확도 99.83%에 해당된다.
(2) 학습 기록 확인하기
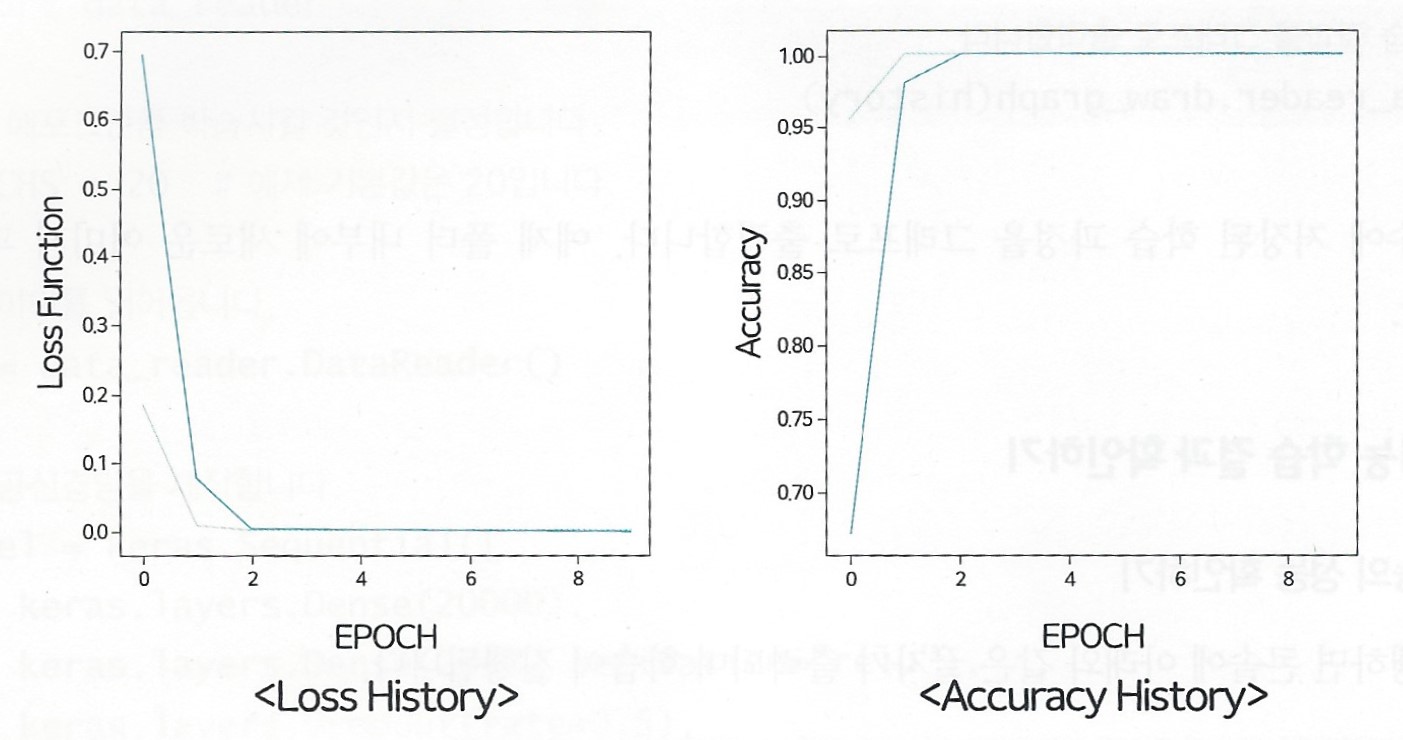
Loss History, Accuracy History 모두 학습 초반에는 큰 폭으로 흔들린다.
학습 후반부에는 로스도 0에 가까운 안정적인 수치가 나오고 정확도도 높은 수준으로 유지
중간중간 정확도 100%를 달성한 적도 있는 만큼, 분류가 잘 되는 문제
이 말은 암 유형에 따른 유전자 발현 패턴에는 굉장히 큰 차이가 있다는 이야기
유전자 발현 패턴이 워낙 다르니, AI가 헷갈리지 않고 정확하게 암을 진단할 수 있었다.
1.7 하이퍼 파라미터 수정하기
이번 예제에서는 입력 데이터 개수가 굉장이 많아 입력층 크기를 크게 만들었다.
2층의 크기는 1층에 비해 적은 편이지만, 만약 2층의 크기를 더 줄이면 성능은 어떻게 변할까
2. BMI 분석을 위한 키, 체중 추론
2.1 프로젝트 소개
앞에서의 X값 피쳐 개수를 줄이고, '몸무게'와 '키'를 동시에 예측하는 인공지능을 만들어본다.
2.2 데이터 살펴보기
가슴 둘레, 소매 길이, 허리 둘레, 샅높이, 머리 둘레, 발 길이 총 6개 피쳐를 X값으로 사용하며,
키와 몸무게를 Y값으로 사용한다.
0부터 1 사이 수치로 노멀라이즈하고,
트레이닝:테스트=8:2로 진행한다.
2.3 어떤 인공지능을 만드나
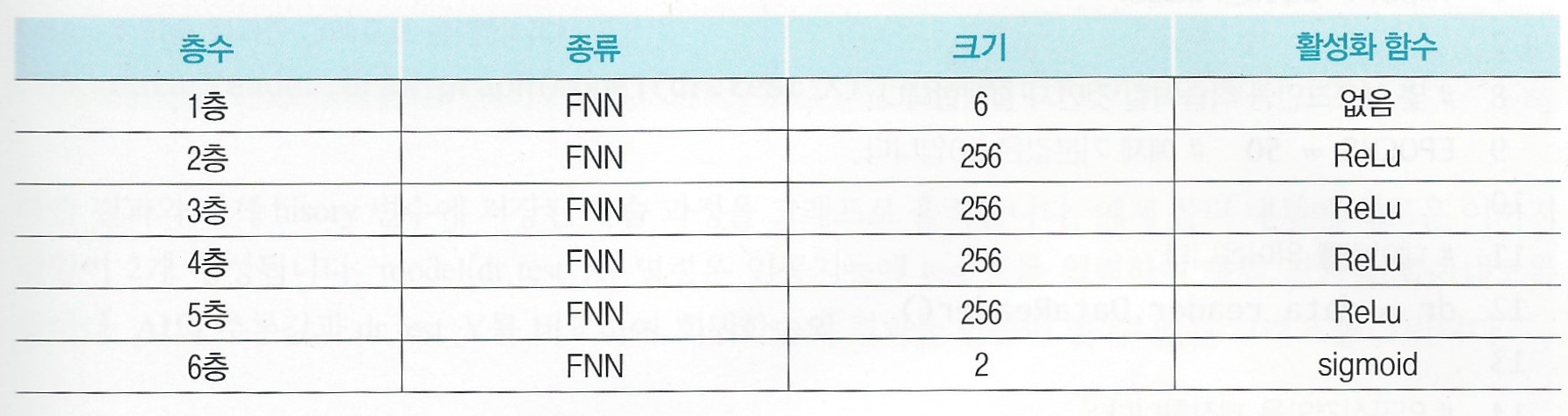
입력층의 크기는 6으로 세팅
2가지 종류 값을 동시에 회귀분석 하기 위해 출력층의 크기를 2로 증가
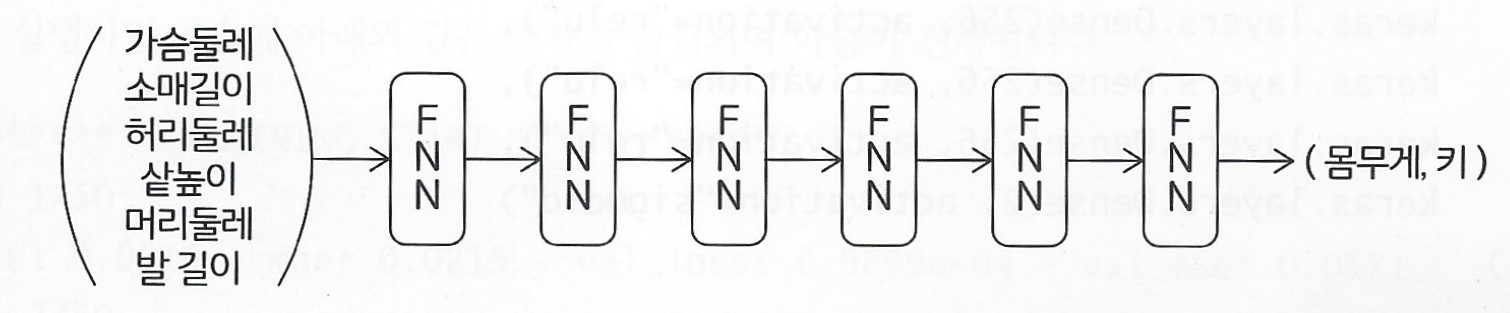
2.4 딥러닝 모델 코딩
from tensorflow import keras
import data_reader
# 몇 에포크 만큼 학습을 시킬 것인지 결정합니다.
EPOCHS = 50 # 예제 기본값은 50입니다.
# 데이터를 읽어옵니다.
dr = data_reader.DataReader()
# 인공신경망을 제작합니다.
model = keras.Sequential([
keras.layers.Dense(6),
keras.layers.Dense(256, activation="relu"),
keras.layers.Dense(256, activation="relu"),
keras.layers.Dense(256, activation="relu"),
keras.layers.Dense(256, activation="relu"),
keras.layers.Dense(2, activation='sigmoid')
])
# 인공신경망을 컴파일합니다.
model.compile(optimizer="adam", loss="mse", metrics=['mae'])이전 FNN 회귀 코드와 크게 다르지 않다.
학습 에포크는 50으로 세팅
optimizer는 adam
loss는 MSE 사용
2.5 인공지능 학습
(1) 인공신경망 학습
# 인공신경망을 학습시킵니다.
print("\n\n************ TRAINING START ************ ")
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
history = model.fit(dr.train_X, dr.train_Y, epochs=EPOCHS,
validation_data=(dr.test_X, dr.test_Y),
callbacks=[early_stop])(2) 학습 결과 출력
# 학습 결과를 그래프로 출력합니다.
data_reader.draw_graph(model(dr.test_X), dr.test_Y, history)model(dr.test_X) 명령은 인공지능에 test_X를 입력하여 출력 결과를 뽑아내도록 한다.
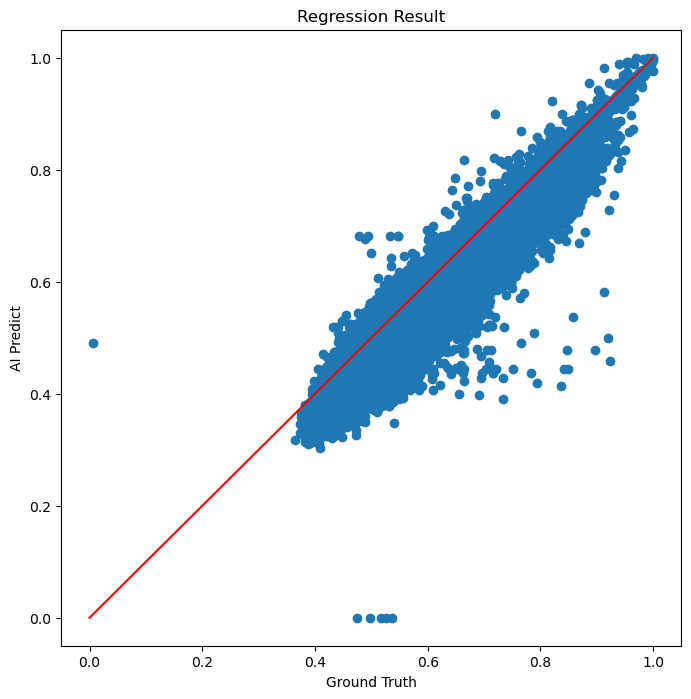
AI의 추론값과 dr.test_Y를 비교하여 회귀학습의 결과를 한눈에 볼 수 있는 그래프를 그린다.
분류 문제에선 data_reader.draw_graph(history)로만 구성되지만,
회귀 문제에선 data_reader.draw_graph(model(dr.test_X), dr.test_Y, history)로 구성된다.
분류의 Accuracy History 그래프가 없어지고,
회귀의 Regression Result 그래프가 생긴다.
2.6 인공지능 학습 결과 학인하기
(1) 인공지능의 성능 확인하기

콜백 작용으로 30에서 학습이 멈췄다.
최종 성능은 MAE 기준, 1.55% 오차 수준
거의 98% 이상 정답에 근접한 수치를 예측할 수 있다는 의미
(2) 학습 기록 확인하기
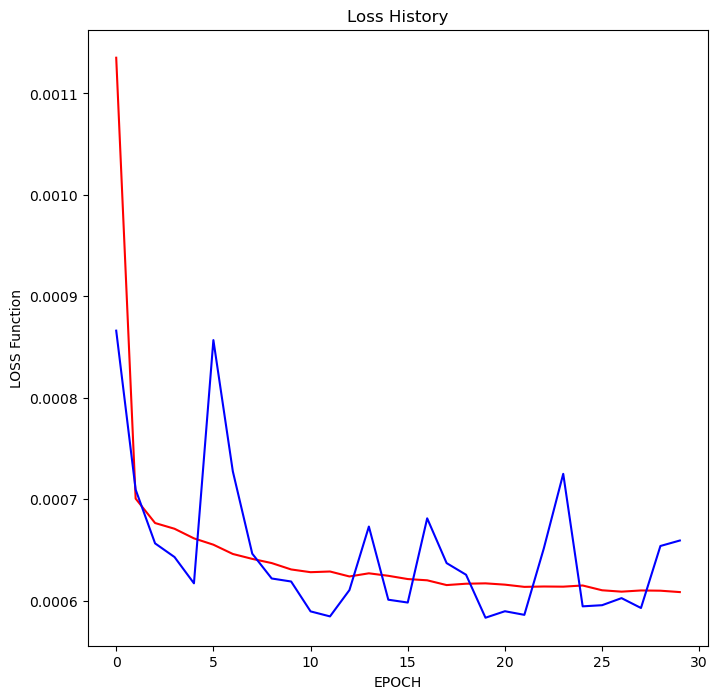
Loss History 그래프의 일부 구간에서 트레이닝 loss보다 테스트 loss가 낮은 값을 보이기도 한다.
회귀 결과 또한 선의 축을 따라 얇게 분포하고 있다.
학습이 잘 된 것으로 파악됨
