피보나치 수열

피보나치 수열은 다음과 같이 정의된다.

• $F_0 = 0$
• $F_1 = 1$
• $F_N = F_{N-1} + F_{N-2}$ $(N = 2,3,...)$

$N$이 3일 때
$F_3 = F_2 + F_1 = (F_1 + F_0) + F_1 = (1+0)+1$
과 같은 재귀함수의 모양이 된다.

로직 구성

피보나치 수열에서 더 이상 나누어지지 않는 것은 $F_1$과 $F_0$이다.

피보나치 수열을 재귀함수로 생각하면 베이스 케이스가 되어 리턴을 시작하는 부분도 $F_1$과 $F_0$이다.

• 베이스 케이스 = $F_1$, $F_0$
• 베이스 케이스 만나기 전까지 하는 호출 = $F_{N-1} + F_{N-2}$

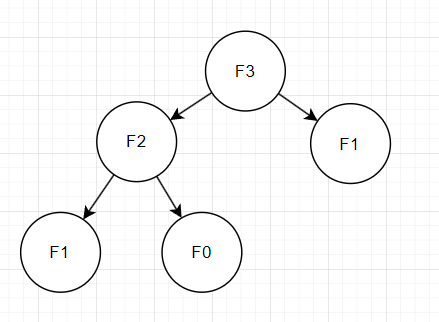
위에 $N$이 3일 때의 예시를 보면
$F_3$일땐 $F_2$와 $F_1$를 필요로 하고, $F_2$일땐 $F_1$과 $F_0$을 필요로 한다.

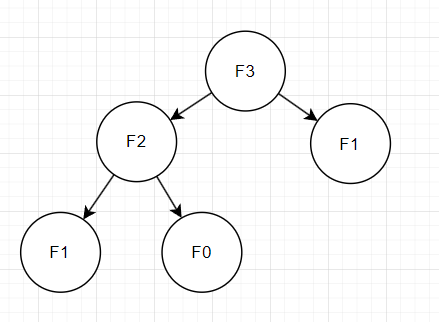
내가 말을 복잡하게 써놔서 난해할 수 있지만 코드를 보면 이해에 도움이 될 것이다.

구현

#include <iostream>
using namespace std;

int Fibo(int N)
{
    //베이스 케이스
    if (N == 0)
        return 0;
    else if (N == 1)
        return 1;

    return Fibo(N-1) + Fibo(N-2);
}

int main()
{
    cout << "Fibo(6) : " << Fibo(6)<< endl;
}

• $F_1$과 $F_0$일땐 1과 0을 리턴해준다.
• N이 2 이상의의 값일 땐 Fibo(N-1) + Fibo(N-2) ($F_{N-1} + F_{N-2}$) 를 베이스 케이스 만나기 전까지 계속 호출해서 베이스 케이스에서 리턴 값을 받아낸다.

위와 같은 구현 방식은 같은 계산을 많이 반복하게 돼서 비효율적이다.
이런 부분을 보완하기 위해서 메모제이션 동적 계획법이 사용된다.
그 내용은 다음에..

---

참고 자료
오츠키 켄스케 , 『문제 해결력을 높이는 알고리즘과 자료구조, 서수환 옮김, 길벗(2022)