[전체 코드]

// 1, 2, 3, 더하기 4
package DynamicProgramming;
import java.util.*;

public class BJ15989 {
    static int t, maxN = 0, MAX_VALUE = 10001;
    static int[][] dp = new int[MAX_VALUE][4];
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        t = sc.nextInt();
        int[] queries = new int[t];

        for (int i = 0; i < t; i++) {
            queries[i] = sc.nextInt();
            maxN = Math.max(maxN, queries[i]);
        } 

        solve(maxN); // maxN을 기준으로 한 번만 호출하여 dp를 완성함.

        for (int n : queries) {
            System.out.println(dp[n][1] + dp[n][2] + dp[n][3]);
        }
    }

    public static void solve(int maxN) {
        // 초기값 
        dp[1][1] = 1;
        dp[1][2] = 0;
        dp[1][3] = 0;
        dp[2][1] = 1;
        dp[2][2] = 1;
        dp[2][3] = 0;
        dp[3][1] = 1;
        dp[3][2] = 1;
        dp[3][3] = 1;

        // 점화식 (필요한 maxN까지만 계산)
        // 조합을 구해야하므로, 오름차순인 경우만 인정한다.
        // 따라서 dp[][]의 2번째 인자가 2일 경우, 1과 2로 끝나는 경우만 구해야 한다. (3으로 끝나는 경우를 구해버리면 오름차순이 깨짐.)
        for (int i = 4; i <= maxN; i++) {
            dp[i][1] = dp[i - 1][1];
            dp[i][2] = dp[i - 2][1] + dp[i - 2][2];
            dp[i][3] = dp[i - 3][1] + dp[i - 3][2] + dp[i - 3][3];
        }
    }
}

[문제 풀이 설명]

이 문제는 9095(1, 2, 3 더하기) 문제를 기반으로 "합을 이루고 있는 수의 순서만 다른 것은 같은 것으로 친다." 의 조건이 더해진 문제이다.

n이 4인 경우를 예로 들면,

1로 끝나는 경우: 1+1+1+1, 1+2+1, 2+1+1, 3+1
2로 끝나는 경우: 1+1+2, 2+2
3으로 끝나는 경우: 1+3

이 전체 경우이지만, 문제의 조건으로 인해서 1+2+1, 2+1+1, 3+1은 제외된다.
따라서 우리는 순열이 아닌 조합인 경우를 구해야 한다.

-> 이 경우 오름차순을 생각해서 구하면 쉽다!

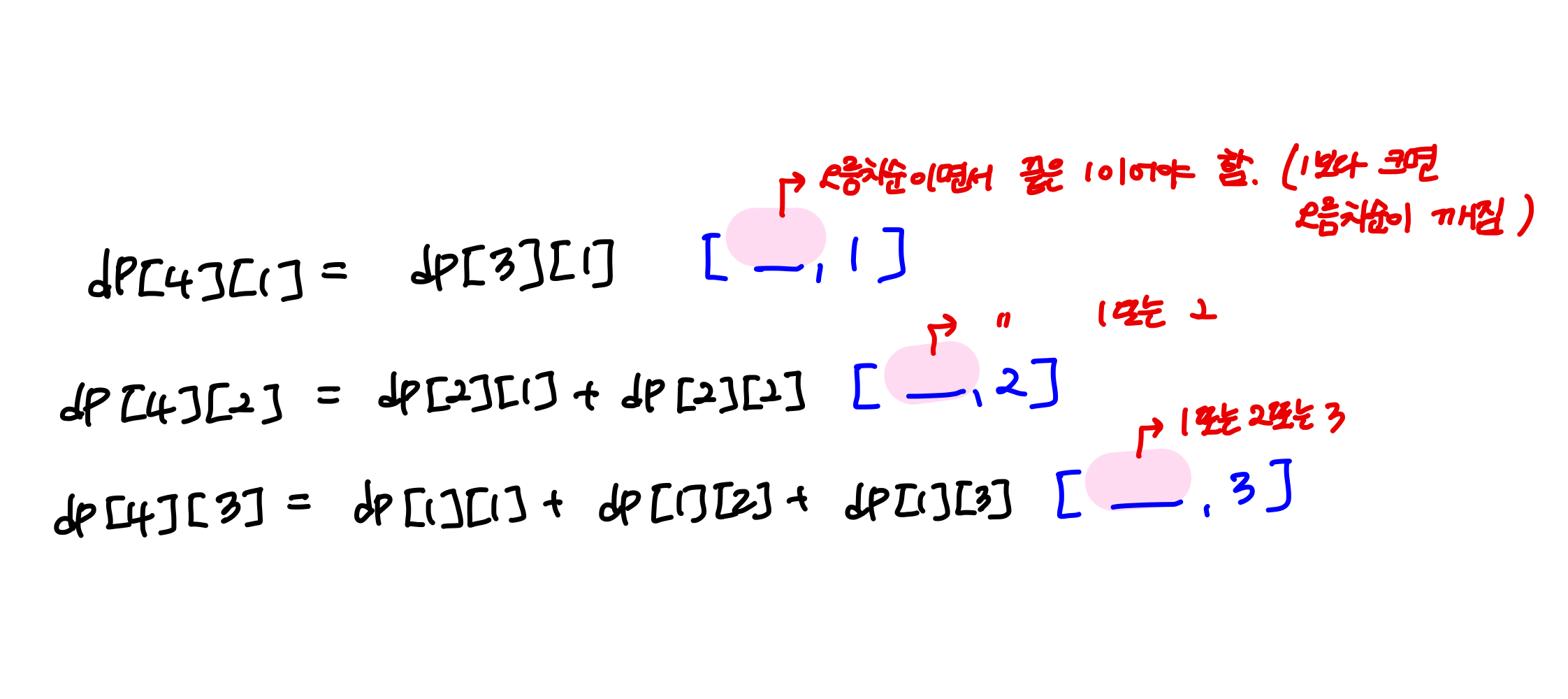
n이 4일 때 1, 2, 3을 각각 마지막인 경우의 수를 각각 구해준다.
1을 마지막이라고 가정한 경우, 그 앞에 올 값들은 오름차순이면서 끝 값이 1이어야 한다.
dp[3][1]이므로, 1+1+1이 될 것이다.

왜 2+1은 안 되냐? dp[3][1]은 점화식을 통해 dp[2][1]과 같다. dp[2][1]이 1+1이므로, dp[3][1]은 결국 1+1+1이 된다. 그리고 오름차순이라는 조건이 있으므로 애초에 2+1은 오름차순을 만족하지 않는다.

이런 규칙으로 점화식을 찾아주면 된다!

[어려웠던 점]

1+2+3 더하기 시리즈 중 제일 어려웠다.
뭔가 중복 체크를 하면서 푸는 건줄 알고 visited 배열을 활용해야 하나,, 했었어서 더 복잡하게 느껴졌었다.

[느낀점]

경우의 수를 모두 보면서 차근 차근 규칙과 조건을 찾아가는 것이 중요한 것 같다.