[전체 코드]
// 이분 그래프
package graphSearh;
import java.util.*;
public class BJ1707 {
static int k;
static ArrayList<ArrayList<Integer>> adjList; // 인접행렬 -> 인접리스트 (메모리 절약)
static int[] visited; // int로 한 이유는, 방문하지 않았으면 무조건 0. color를 구분하기 위하여 1과 -1를 사용하기 위함.
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 입력
k = scanner.nextInt(); // test case의 개수
for (int i = 0; i < k; i++) {
int v = scanner.nextInt();
int e = scanner.nextInt();
adjList = new ArrayList<>(); // 인접리스트 초기화
visited = new int[v]; // visited 초기화
for (int j = 0; j < v; j++) {
adjList.add(new ArrayList<>());
}
// 간선 수 만큼 간선 입력받기
for (int j = 0; j < e; j++) {
int a = scanner.nextInt() - 1;
int b = scanner.nextInt() - 1;
adjList.get(a).add(b); // 양방향 연결
adjList.get(b).add(a);
}
// 비연결 그래프일 수도 있으니, 방문하지 않은 모든 정점에서 함수 실행해야 함.
boolean isFalse = true;
for (int j = 0; j < v; j++) {
if (visited[j] == 0) {
if (!bfs(j, v)) {
isFalse = false;
break;
}
}
}
System.out.println(isFalse ? "YES" : "NO");
}
}
public static boolean bfs(int start, int n) { // 시작 좌표, graph 크기
visited[start] = 1; // 1로 체크.
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
// queue가 빌 때까지
while (!queue.isEmpty()) {
int curVertex = queue.poll(); // 정점 번호.
// curVertex와 이웃한 노드 찾기
for (int nextVertex : adjList.get(curVertex)) {
// 방문하지 않았다면
if (visited[nextVertex] == 0) {
visited[nextVertex] = -visited[curVertex];
queue.add(nextVertex);
}
// 방문했다면
else {
// 현재와 같은 색상이면 false
if (visited[curVertex] == visited[nextVertex]) {
return false;
}
}
}
}
return true;
}
}
[문제 풀이 설명]
🔎 이분 그래프란?
일단! 이 문제를 풀기 전에, 당연히 이분 그래프가 무엇인지부터 간단하게 살펴보자.
*이분 그래프란?
인접한 정점끼리는 서로 다른 색상 -> 모든 정점을 2가지 색으로만 칠할 수 있는 그래프.
한 마디로, 이웃하고 있는 정점끼리는 같은 색상이면 안 된다.
그리고 여기서 중요한 점!!
비연결 그래프도 이분 그래프가 될 수 있다.
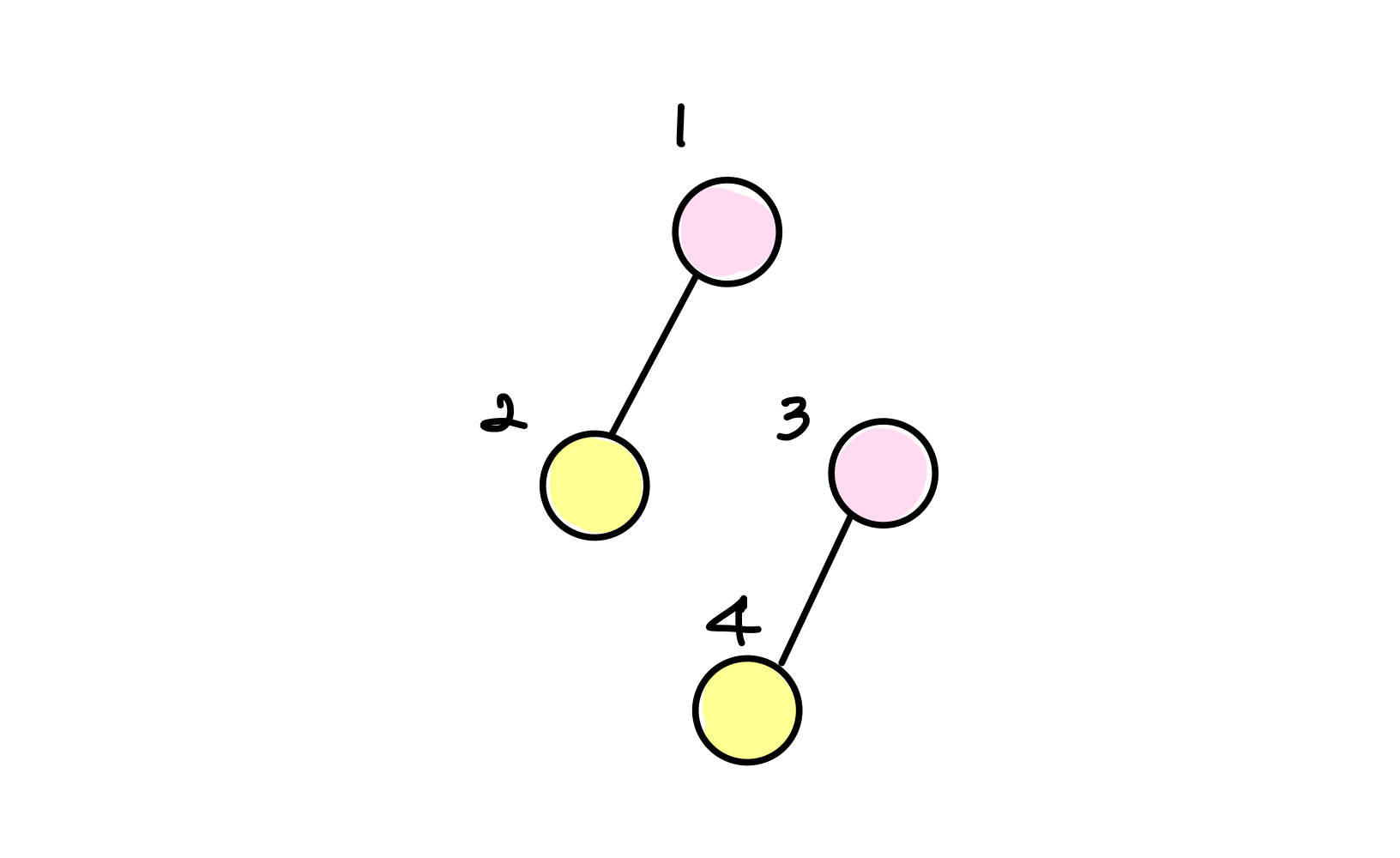
위 사진처럼, 비연결 그래프도 이분 그래프가 될 수 있다는 것을 명심하자.
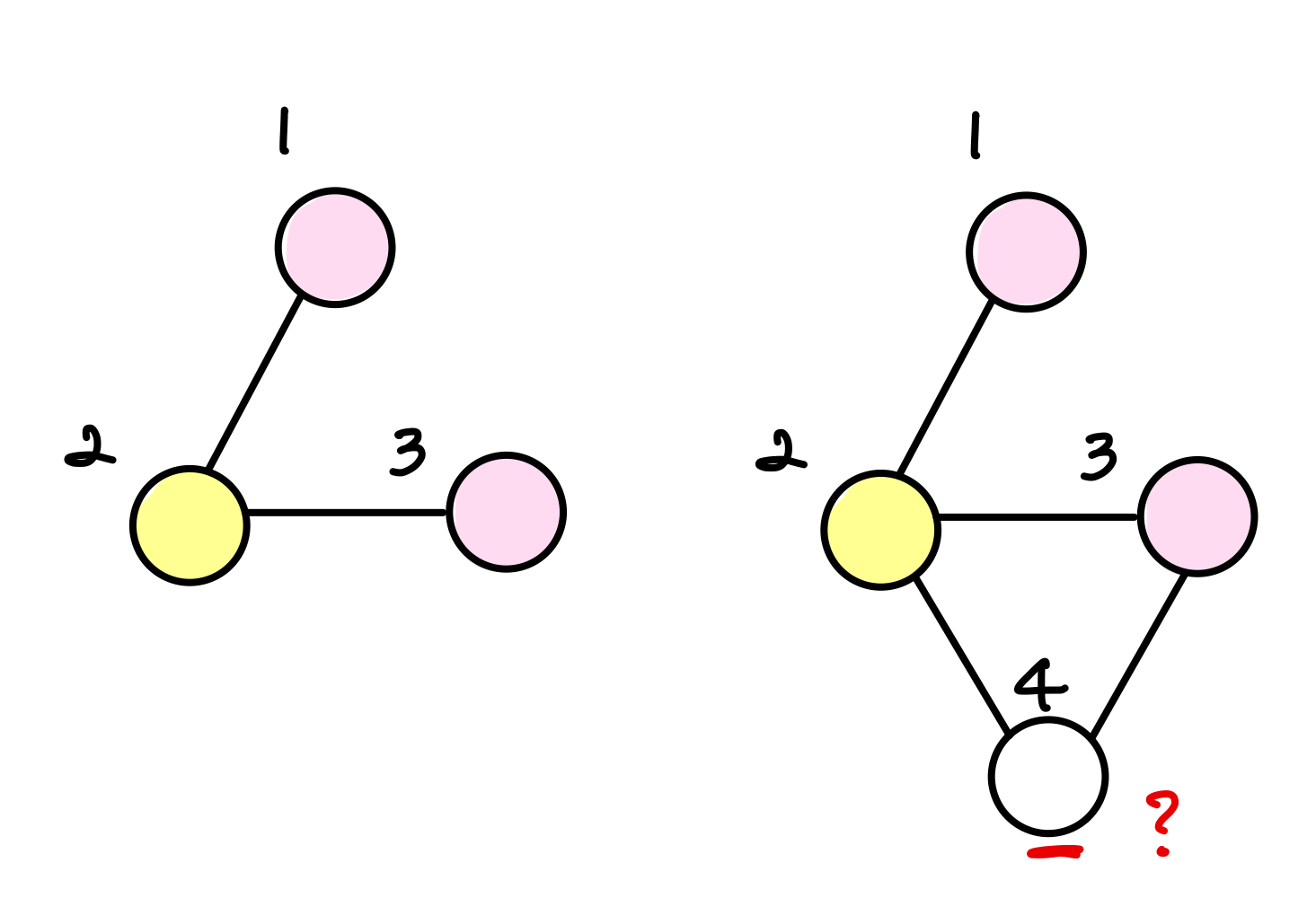
위 그림은 이분 그래프를 이해하기 쉽게 예제 입력 1의 상황을 그려본 것이다.
왼쪽 상황은 "YES"가 출력되고, 오른쪽 상황은 "NO"가 출력된다.
오른쪽 상황의 경우, 2는 3과 4와 인접하고 있다. 만약 4에 노랑색을 칠한다면 그럼 3과 4는???
4는 3과도 인접하고 있기 때문에 핑크색이 아닌 노랑색이어야 하는데,, 따라서 이 그래프는 이분 그래프가 아니므로 "NO"가 출력이 된 것이다.
☝🏻 그래서 어떻게 푸냐
dfs나 bfs로 그래프를 탐색하면서, 나와 이웃하고 있는 정점의 색상이 나와 같으면 false를 반환하면 된다!
[어려웠던 점]
2가지가 있다.
☝🏻첫 번째는, 인접 행렬로 풀었기 때문에 메모리 초과가 뜬 것이었다.
분명 알고리즘 수업 때, 인접 행렬과 인접 리스트에 대해서 배웠는데 그새 까먹었ㅇ..
인접 행렬을 이용하면, Worst Case의 경우 v가 20,000일 때, 인접 행렬은 총 400,000,000칸이 되고, int가 4byte이니, 4byte * 400,000,000 = ?? 따라서, 백준 메모리가 제한된다. 따라서 이 문제점은 인접 리스트를 사용하여 해결하였다.
✌🏻두 번재는, main함수에서 bfs를 호출할 때 bfs(0) 이렇게만 해주었다.
아까 말했듯이, 비연결 그래프도 이분 그래프에 해당될 수 있으므로, (방문하지 않은) 모든 정점에서 bfs를 실행해야 한다.
정점 0번에서만 실행하면 연결되지 않은 노드들은 탐색하지도 않기 때문이다! 이 문제점은 for문을 사용하여서 방문하지 않은 정점들을 탐색하도록하여 해결하였다.
[느낀점]
코테 언어를 java로 바꾼 후, 아직 문법에 익숙치가 않다.
특히 인접 리스트로 구현하는 코드 복습해야겠다.