깊이 우선 탐색 (Depth First Search)
- 한 정점에서 시작해서 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면, 다시 가장 가까운 갈림길로 돌아와서 이곳으로 부터 아직 방문하지 않은 정점을 다른 방향으로 탐색하는 방법
- 모든 정점을 방문하고자 하는 경우 사용
- 어떤 노드를 방문했었는지 여부를 반드시 검사
- 스택 OR 재귀를 이용해 구현
- 너비우선탐색(BFS)보다 더 간단
- 검색 속도는 BFS 보다 느리다
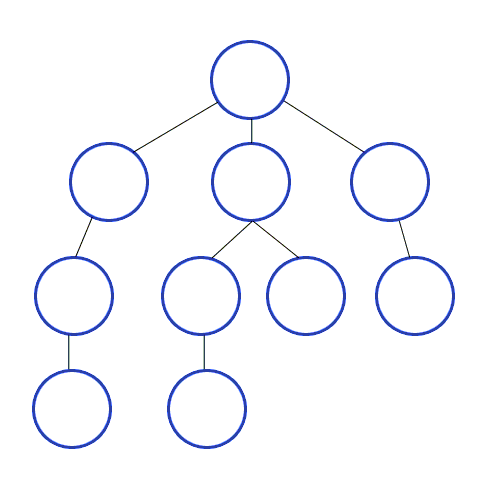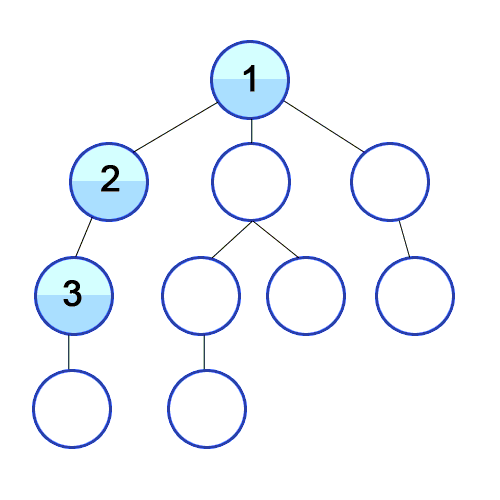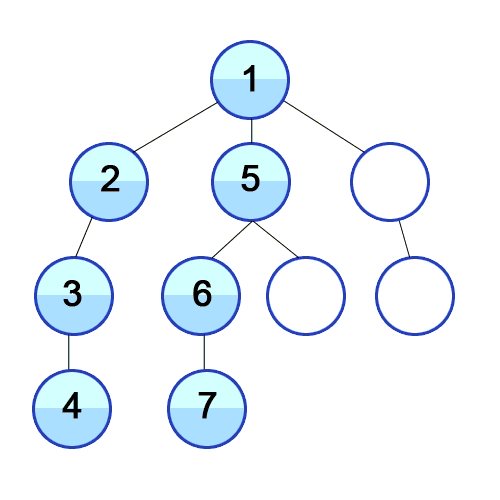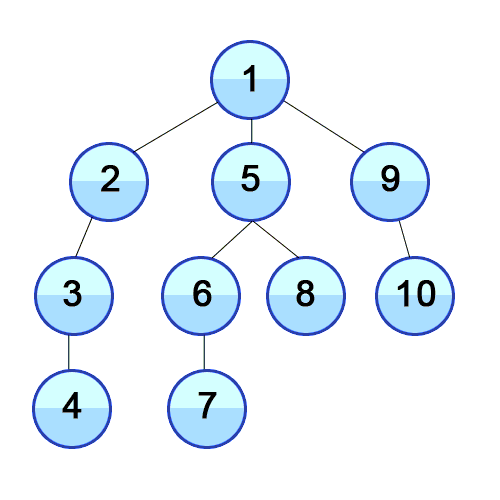
// dfs, 재귀, 인접 행렬, i 정점부터 시작한다.
public static void dfs(int i) {
visit[i] = true;
System.out.print(i + " ");
for(int j=1; j<n+1; j++) {
if(map[i][j] == 1 && visit[j] == false) {
dfs(j);
}
}
}- 시간 복잡도
- 인접 행렬 : O(V²)
- 인접 리스트 : O(V+E)
- V : 점점, E : 간선
너비 우선 탐색 (Depth First Search)
- 한 정점에서 시작해서 인접한 정점을 모두 방문한 다음 첫번째로 연결 된 정점으로 가서 그것과 연결된 정점들을 방문하고 다음으로 나머지 정점들을 방문하여 동일한 동작을 반복하는 방법
- 두 정점사이에 최단 경로를 찾고자 할 때 사용
- 선입선출 원칙으로 탐색으로 큐를 이용하여 구현
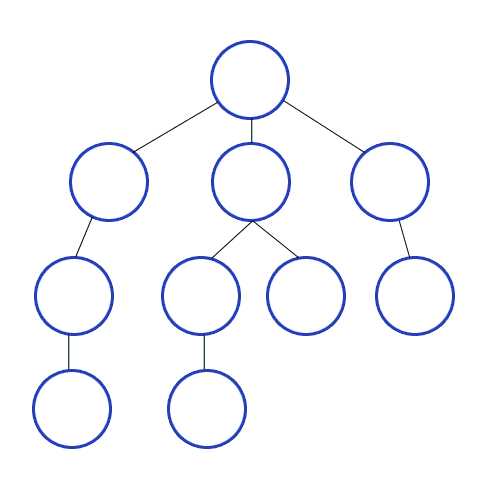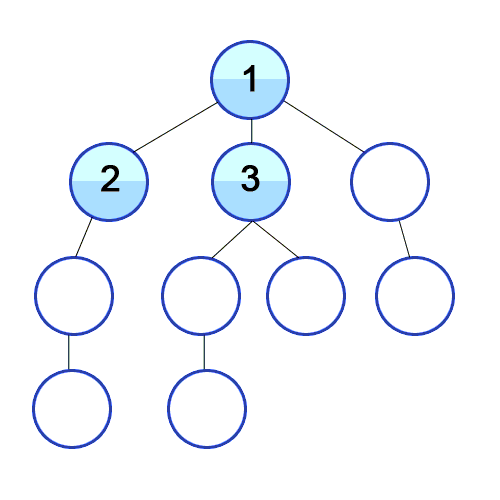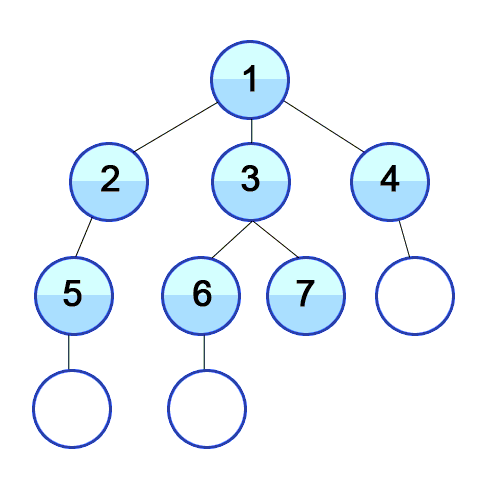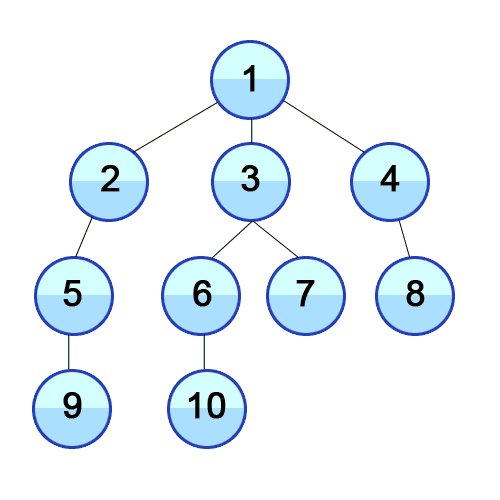
// bfs, q사용, 인접행렬, i 정점부터 시작한다.
public static void bfs(int i) {
Queue<Integer> q = new LinkedList<>();
q.offer(i);
visit[i] = true;
while(!q.isEmpty()) {
int temp = q.poll();
System.out.print(temp + " ");
for(int j=1; j<n+1; j++) {
if(map[temp][j] == 1 && visit[j] == false) {
q.offer(j);
visit[j] = true;
}
}
}
}- 시간 복잡도
- 인접 행렬 : O(V²)
- 인접 리스트 : O(V+E)
- V : 점점, E : 간선
정리
- 모든 정점을 방문해야하는 문제, 경로의 특징을 저장해야 하는 문제 -> DFS
- 최단경로를 구해야 하는 문제 -> BFS
출처
New, Strange, Want to try