그리디 알고리즘

그리디 알고리즘, 탐욕 알고리즘은 최적해를 구하는 데 사용되는 방법이다.
최적화 문제(optimization)에 사용되는 최대 혹은 최소 해를 찾는다.
여러 경우 중 하나를 선택할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행되며 해답에 도달한다.
각 선택 시점에서 이루어지는 결정은 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적인 해답을 만들었다고 하여 그것이 최적이라는 보장은 없다.
일단 한번 선택된 것은 번복하지 않는다. 이때문에 대부분의 탐욕 알고리즘들은 단순하며, 또한 제한적인 문제들에 적용된다.

거스름돈

대표적인 문제로 거스름돈 주기가 있다.

물건값: 1200원
받은돈: 2000원
거스름돈: 800원

이 때 거스름돈으로 주는 최적해는 500원 1개, 100원 3개이다

https://www.acmicpc.net/problem/14916
백준 거스름돈 문제로 풀어보자

public class boj_14916 {
    public static void main(String[] args) throws IOException {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        int cnt = 0;
        boolean isAns = false;
        while(n >= 0){
            // 5로 나누어 떨어지면 바로 답 출력
            if(n % 5 == 0){
                System.out.println(cnt + n/5);
                isAns = true;
                break;
            }
            // 안되면 2씩 뺀다
            n -= 2;
            cnt++;
        }
        if(!isAns){
            System.out.println(-1);
        }
    }
}

2를 계속 빼다가 5로 나누어 떨어지면 답을 출력한다. 반복문 조건이 n>0이 아니라 n>=0인 이유는 거스름돈으로 다 주고 n이 0이 됐을 때 if(n%5==0) 조건에 걸리게 하기 위해서다. 반복문 안에서 n이 0이 안되면 5랑 2로 조합이 안되는 것이니 isAns를 둬서 불가능한 경우 -1을 출력하게 했다.

다른 블로그에서 대박 간단한 코드를 찾아서 공유한다.

https://foxtrotin.tistory.com/319

    public static void main(String[] args) throws IOException {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        int cnt = 0;
        if(n == 1 || n == 3){
            System.out.println(-1);
            return;
        }
        if(n % 5 % 2 == 0){
            cnt = n / 5 + n % 5 / 2;
        }else{
            cnt = n / 5 + (n%5 + 5)/2 - 1
        }
        System.out.println(cnt);
    }

5랑 2모두 나눠떨어지면 5원을를 더 쓰는게 이득이므로 먼저 나눠주고 남은 돈을 2로 거슬러준다.
이 코드가 cnt = n/5 + n%5/2

n이 6, 13같이 이도저도 아니면 else로 빠지는데 이걸 이해하기 힘들었다.

n을 5로 나누면 나머지가 0,1,2,3,4가 나온다

나머지가 2,4일 경우 5로 거슬러준 나머지를 2로 전부 주면 되기 때문에 n%5/2를 더해주면 된다.
예를 들어 n=9일 경우 (거스름돈/5) + (거스름돈%5/2) = 1+2 = 3이 된다

나머지가 1,3일 경우 2로 안나눠지므로 5원 동전을 하나 덜 사용해서 6, 8로 만들어주고 2로 나눠줘야 한다.
예를 들어 n=13이면 5원 1개, 2원 4개로 5개가 답이다.
(거스름돈/5 - 1) + (거스름돈%5 + 5)/2 - 1= 1+4-1 = 4

배낭 짐싸기(Knapsack)

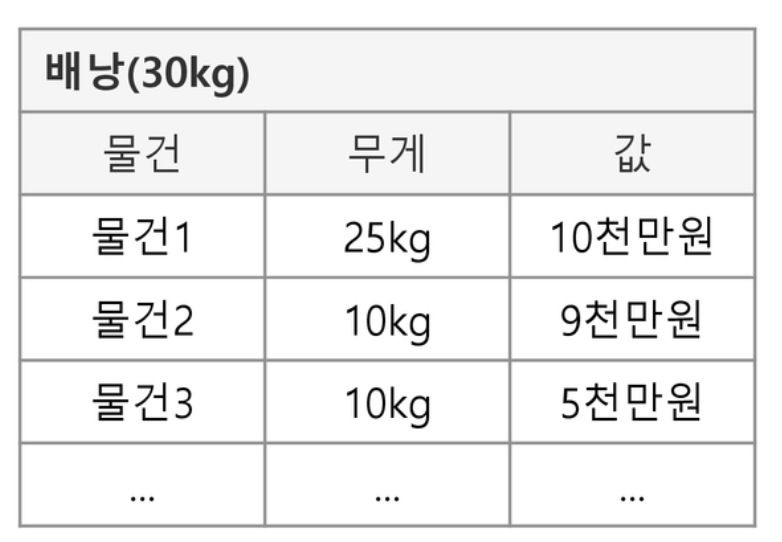
많이들 들어본 문제다. 도둑은 훔친 물건을 배낭에 담아오려고 하는데 배낭 무게가 제한되고 물건의 무게와 가치가 정해져 있다. 그 때 훔친 물건값이 최대가 되는 문제다.

배낭 무게: 30kg
물건1: 25kg, 10원
물건2: 10kg, 9원
물건3: 10kg, 5원

답: 물건2+물건3 = 9원+5원 = 14원이 답이다.
(물건이 각 한개씩만 있다고 가정)

Knapsack에 2가지 종류가 있는데 탐욕법 최적해를 구하려면 Fractional knapsack만 가능하다. 0-1 knapsack은 dp로 풀 수 있다.

1. 0-1 Knapsack
   • 물건을 못쪼개는 경우
2. Fracktional Knapsack
   * 물건을 쪼갤 수 있는 경우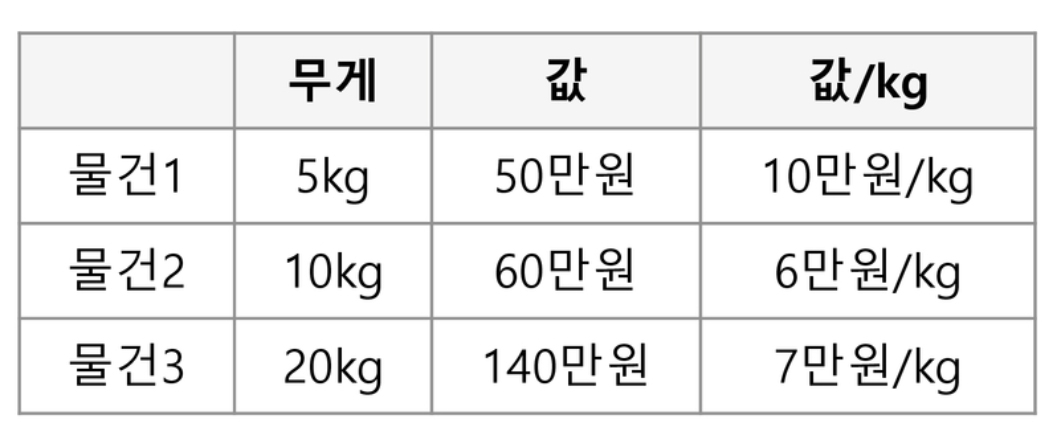
   Fractional knapsack일 때 간단하게 생각하면 배낭 안에 키로당 비싼 물건을 많이 넣으면 된다.
   그럼 kg당 값을 계산해서 배낭 무게에 맞추면 된다. 배낭이 30kg라 했을 때
   물건1(50) + 물건3(140) + 물건2의절반(30) = 220만원이 정답