Asymmetric Key Cryptography
Problems of Symmetric Key Cryptography
- Number of keys
- Symmetric key cryptography needs a shared secret key between two parties.
- For n people, we need n(n-1)/2 shared secret keys.
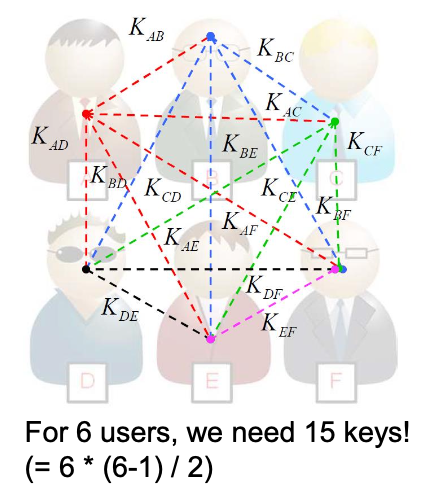
- Key distribution
- Since the secret key of symmetric key cryptography must be shared by both sender and receiver.
- Thus, the symmetric key cryptography needs a secured key distribution protocol.
→ Asymmetric key cryptography!
Asymmetric Key Cryptography
- Asymmetric key cryptography uses two separate keys: one private and one public.
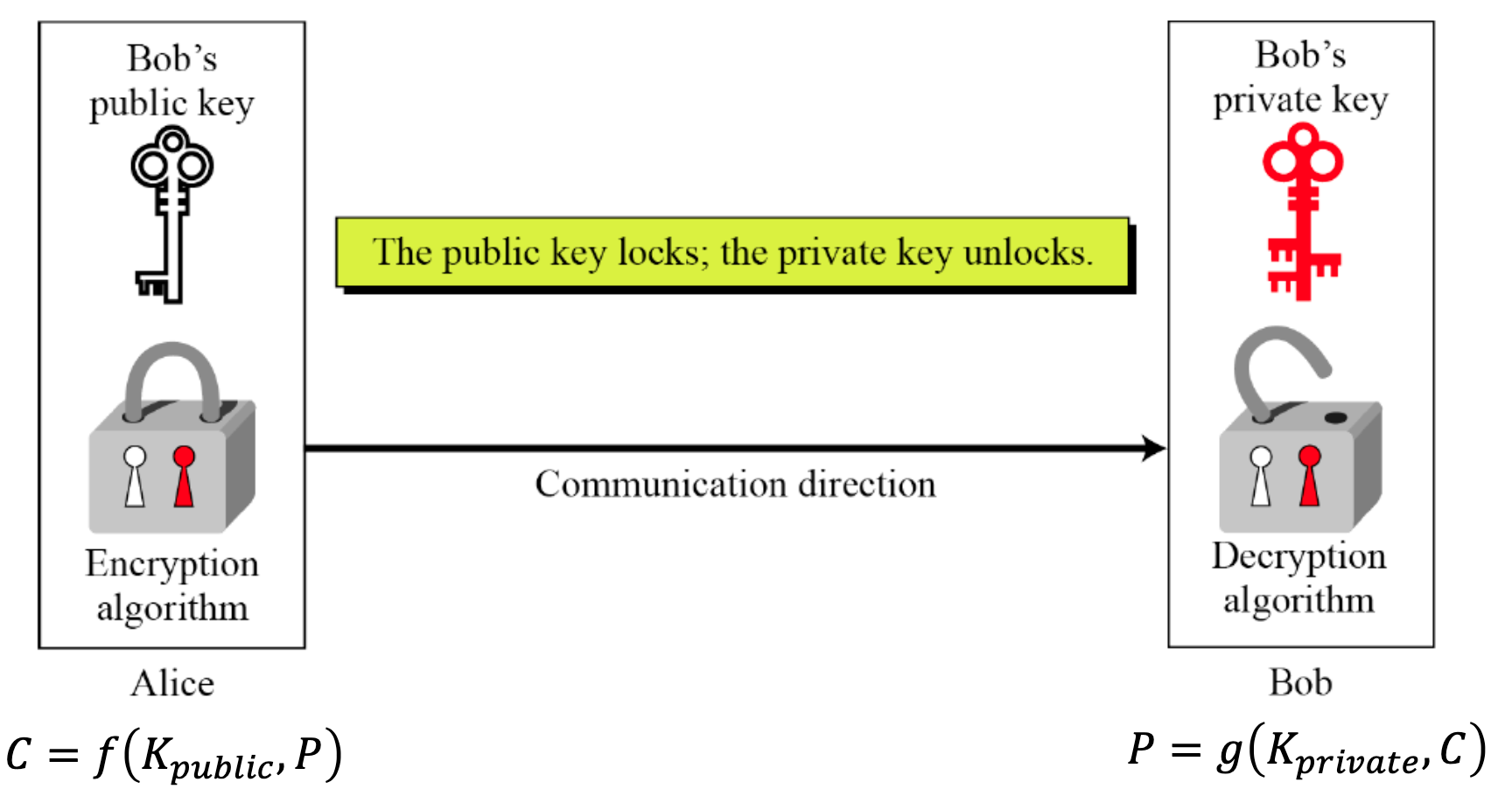
- Example
- Consider a bank and its customers
- Customers encrypt their messages with bank’s public key
- Bank decrypts messages with its private key
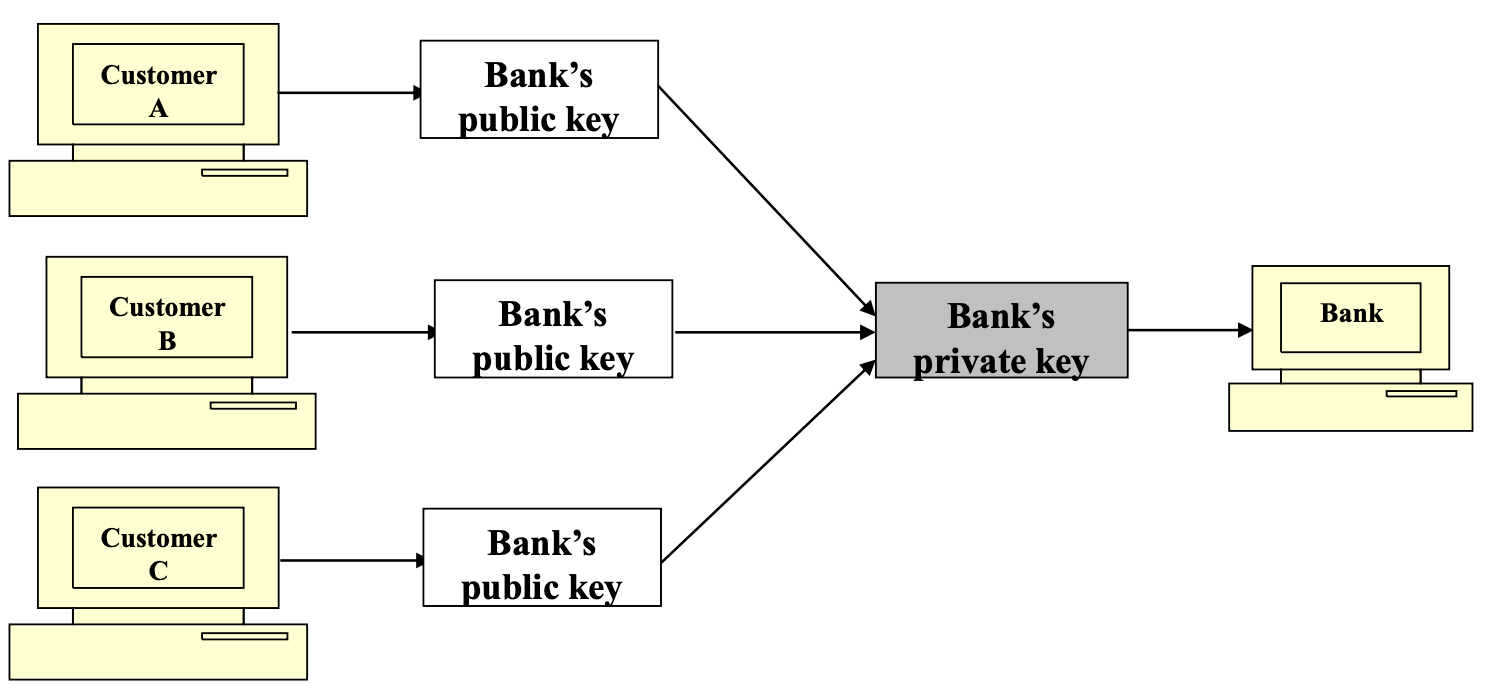
- Asymmetric key cryptography also known as public key cryptography
- Asymmetric key cryptography are complements to the symmetric key cryptography.
- Symmetric- and asymmetric-key cryptography will exist in parallel and continue to serve the community.
- Public key cryptography was invented by Whitfield Diffie and Martin Hellman at Stanford University in 1976.
- Paper “New Directions in Cryptography”
- They won the 2015 Turing Award
Symmetric Key vs. Asymmetric Key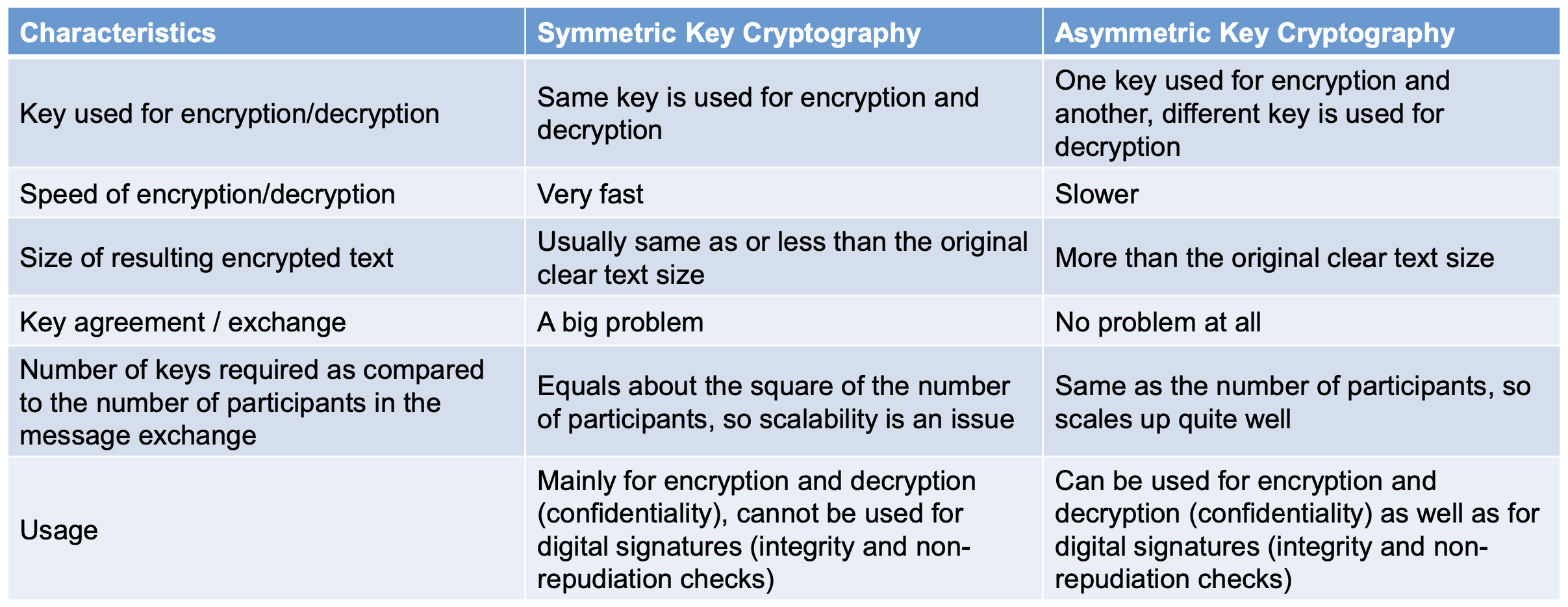
The Best of Both Worlds
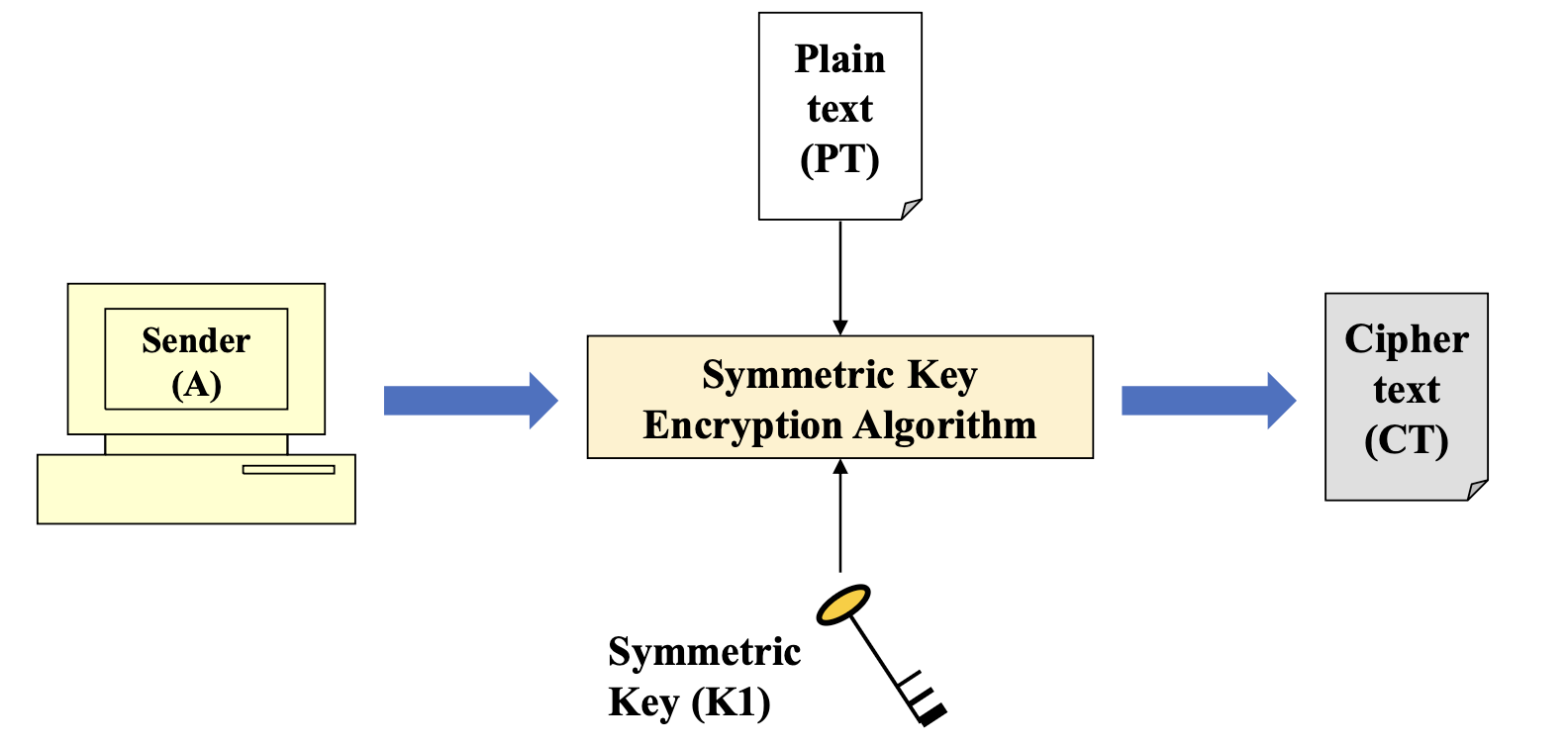
- Encrypting the plaintext with a symmetric-key algorithm
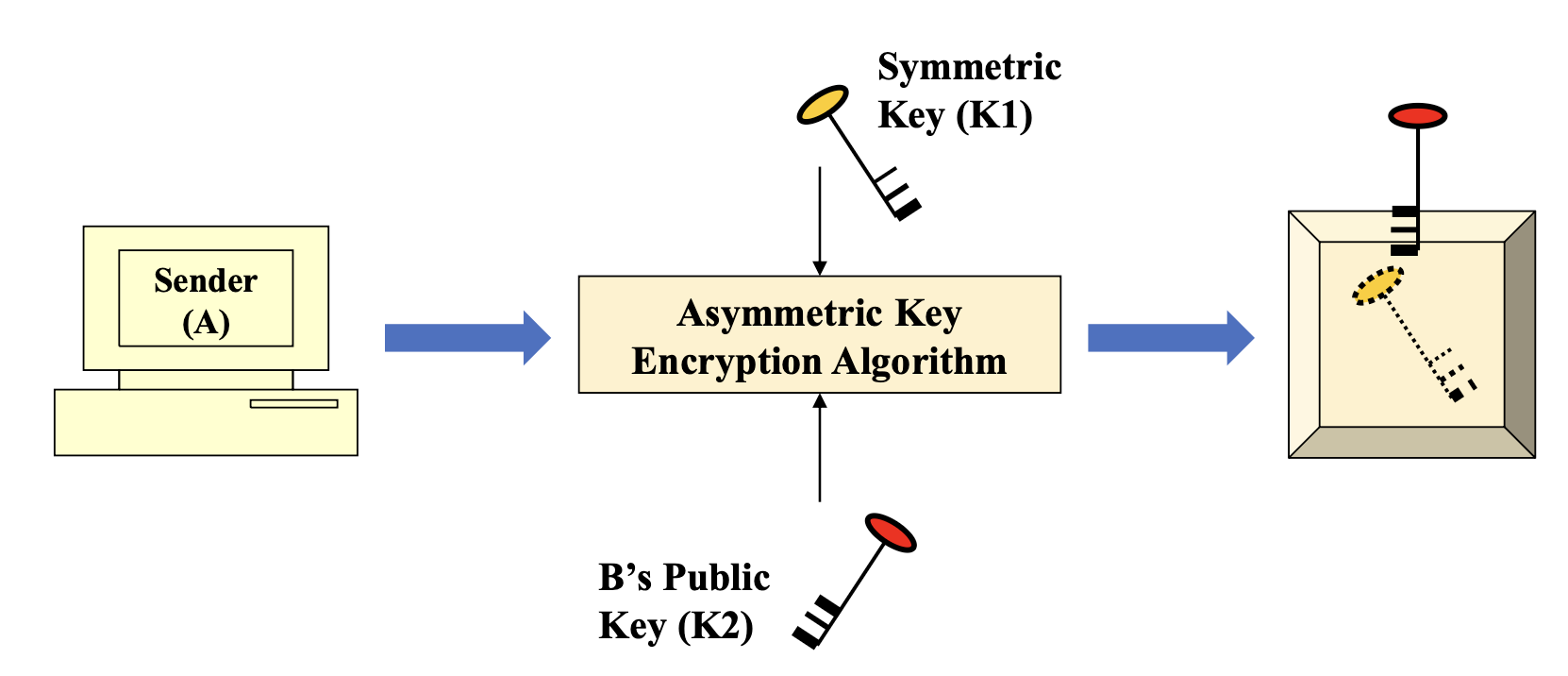
- Symmetric-key wrapping using the receiver’s public key
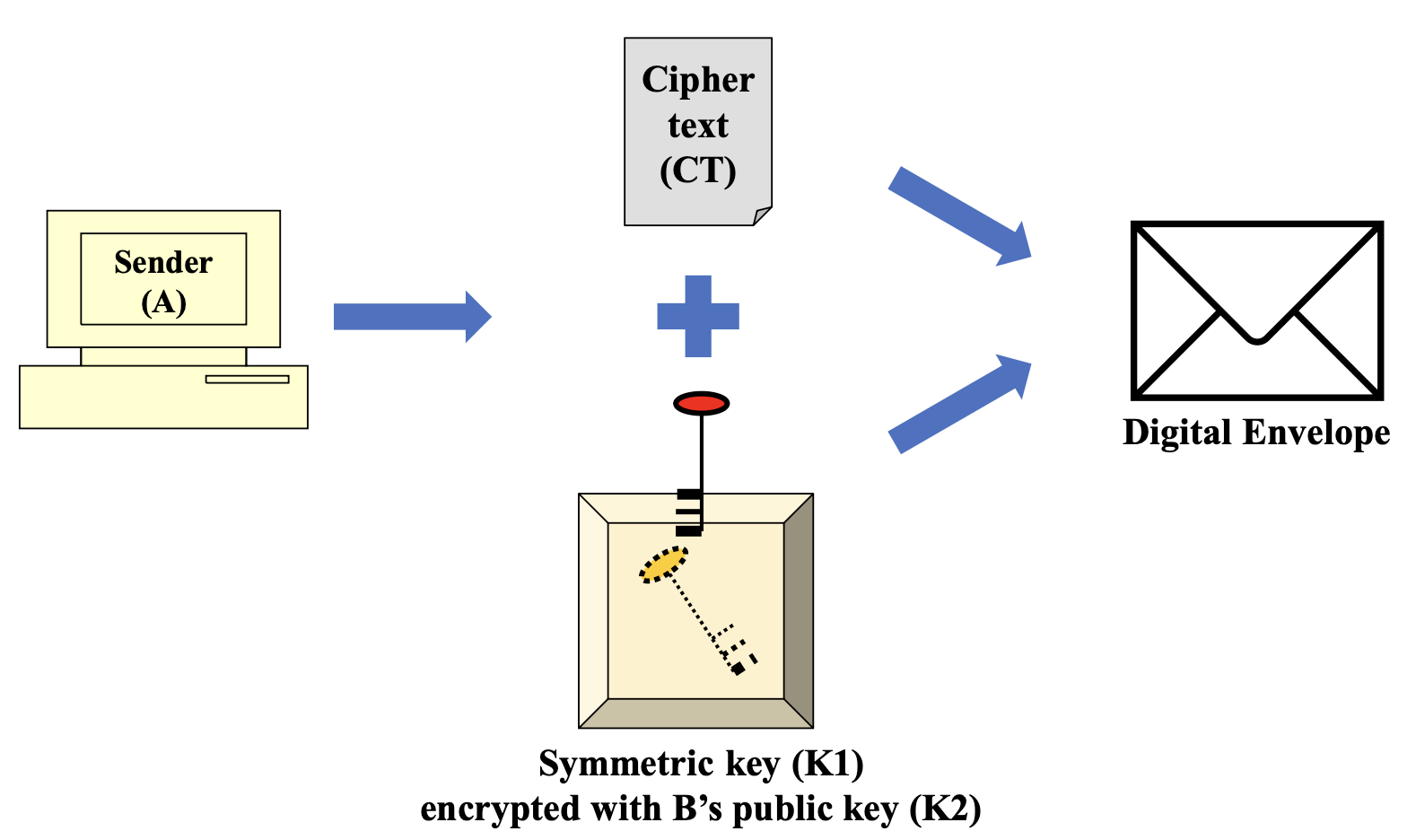
- Digital envelope
- Digital envelope reaches B over the network
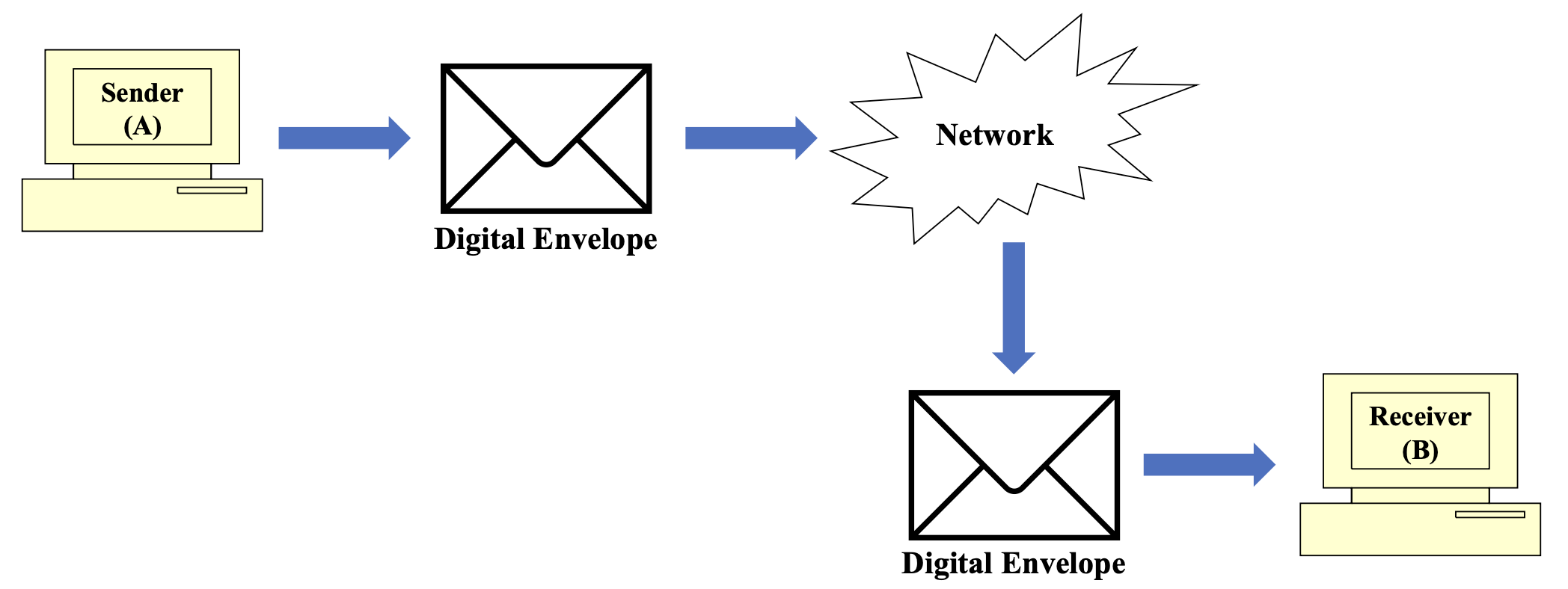
- B opens the digital envelope
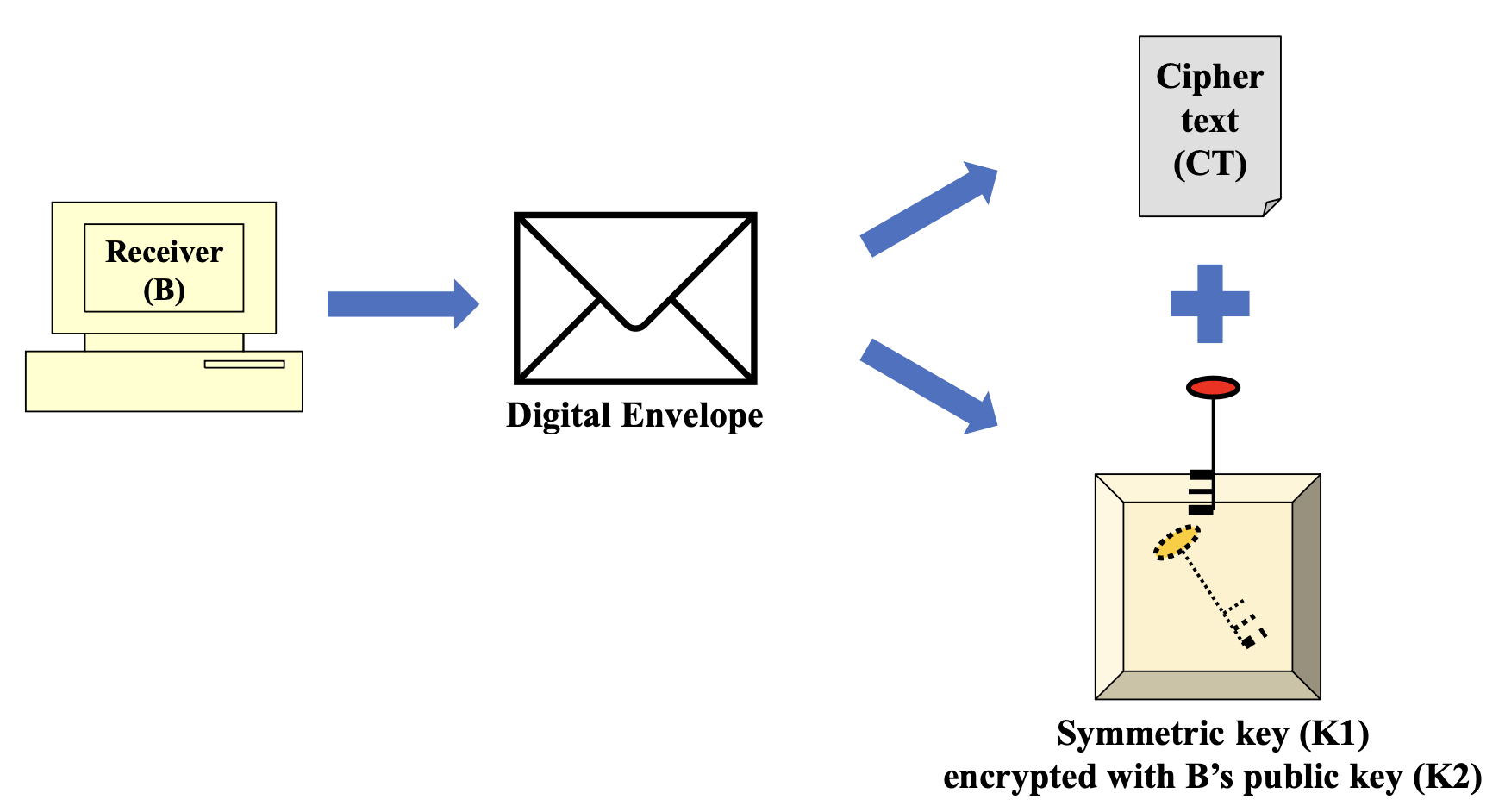
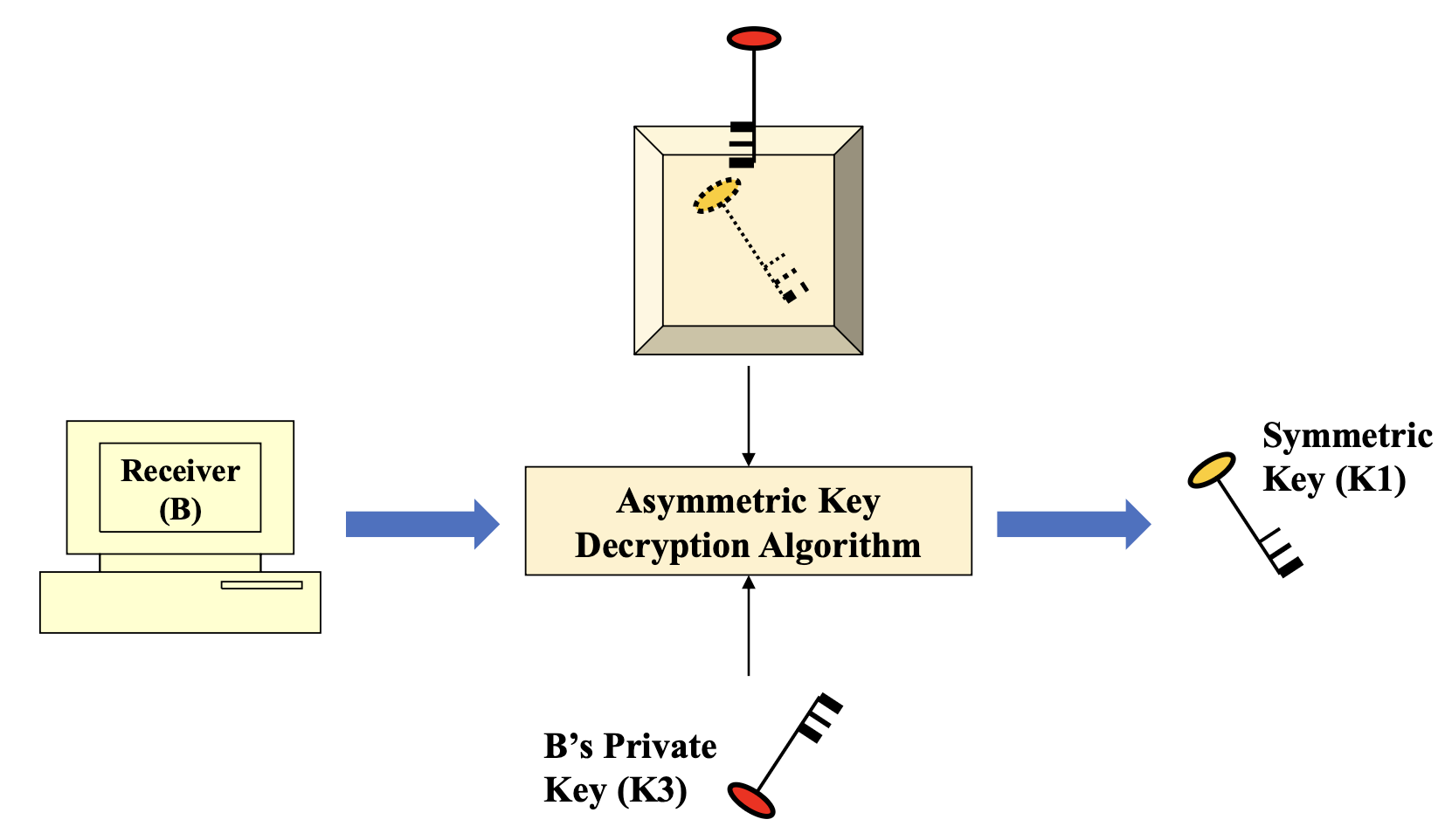
- Retrieval of symmetric key using B’ private key
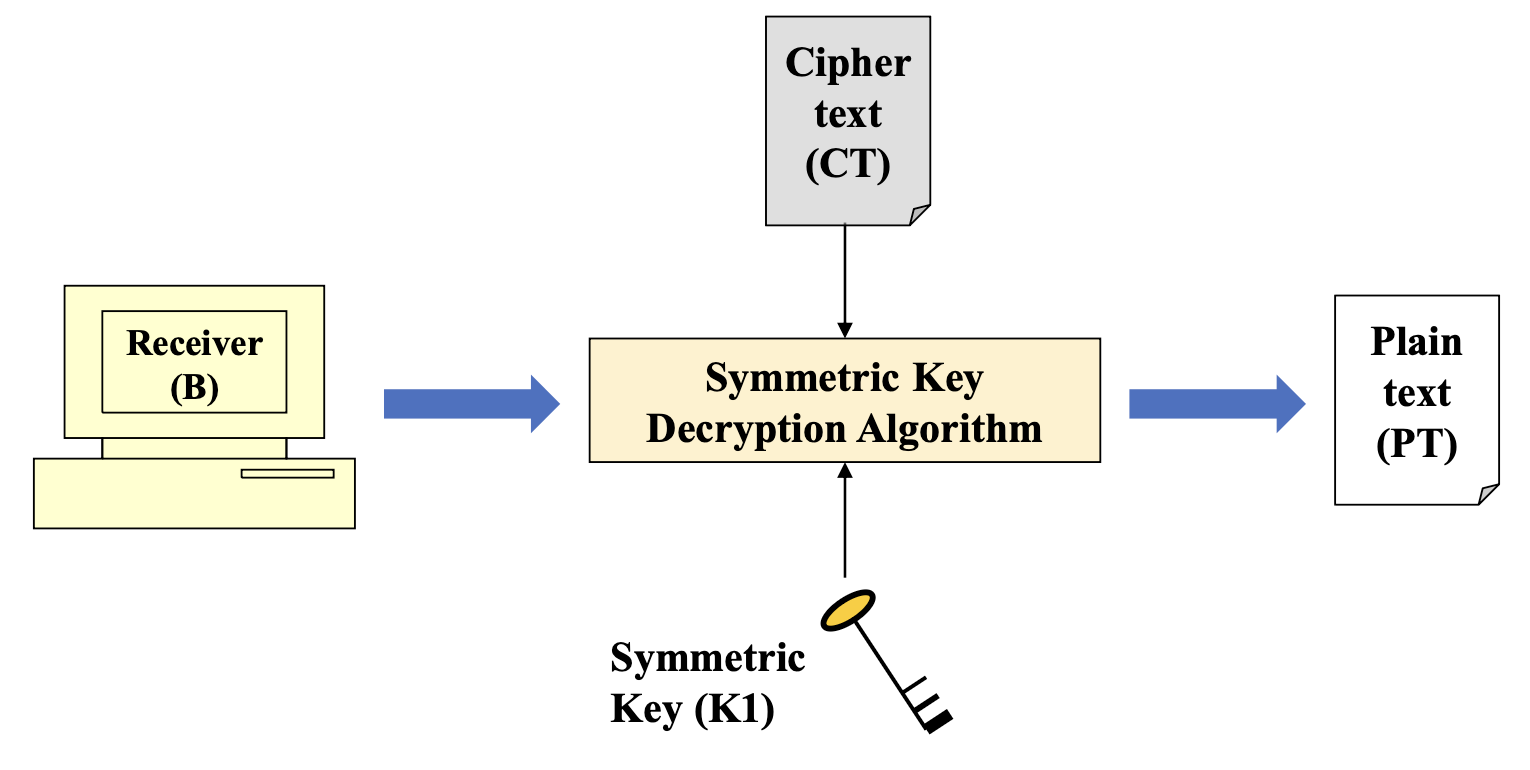
- Retrieval of the original plain text using symmetric key
The RSA Algorithm
- World’s most popular asymmetric key cryptography algorithm
- RSA comes from the surnames of Ron Rivest, Adi Shamir and Leonard Adleman, who publicly described the algorithm in 1977.
- Based on the theory of Prime Numbers
 In RSA, 𝑃 and 𝑄 must be at least 512 bits; 𝑁 must be at least 1024 bits
In RSA, 𝑃 and 𝑄 must be at least 512 bits; 𝑁 must be at least 1024 bits
- Example
- Suppose P=7 and Q=17 → N=PxQ=119

- Suppose P=7 and Q=17 → N=PxQ=119
Modular Arithmetic
- In modular arithmetic, we are interested in only one of the outputs, the remainder 𝑟
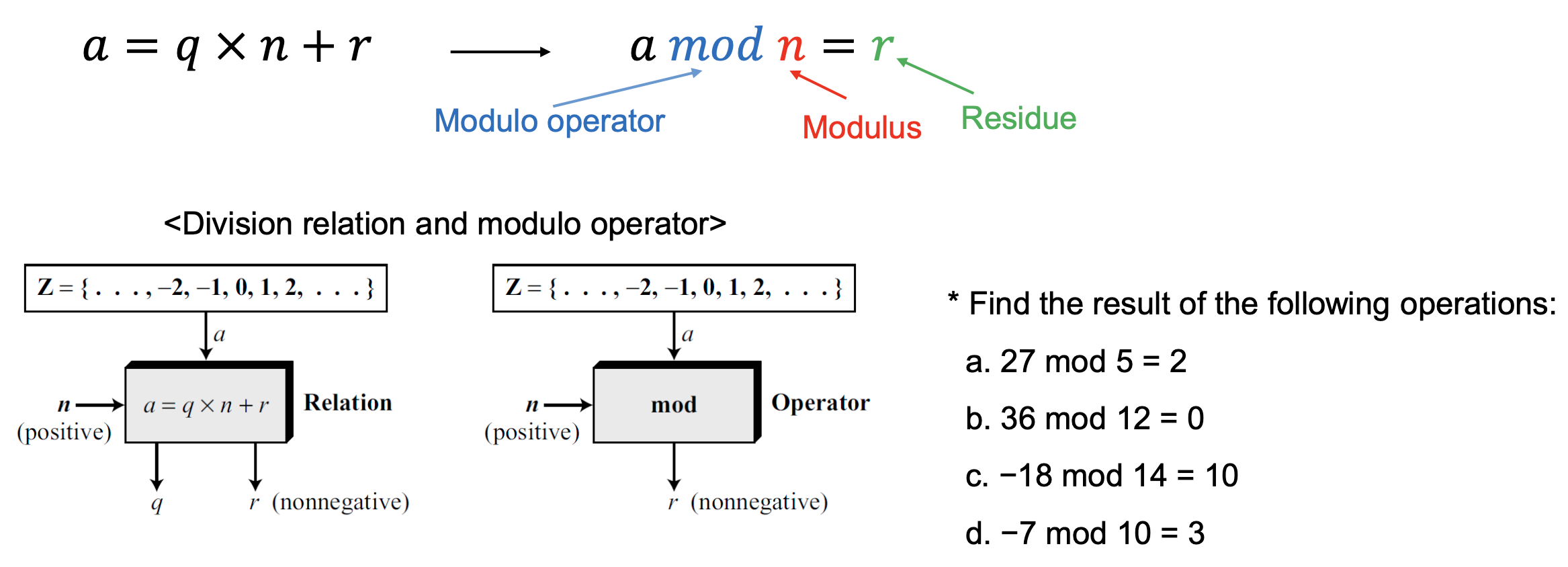 → c. -18 = -2 x 14 + 10
→ c. -18 = -2 x 14 + 10
→ d. -7 = -1 x 10 + 3 - Congruence
- In cryptography, we often used the concept of congruence instead of equality
- To show that two integers are congruent, we use the congruence operator (≡)

- Properties

Euler’s Phi-Function
- Euler’s phi-function, 𝜙(𝑛), which is sometimes called the Euler’s totient function , plays a very important role in cryptography.
- The function finds the number of integers that are both smaller than 𝑛 and relatively prime to 𝑛

- For example, if 𝑛 can be factored as 𝑛 = × × ⋯ × , then we combine the third and the fourth rule to find
𝜙(𝑛) = 𝜙( × × ⋯ × )
= (− ) × (− ) × ⋯ × (− )
- For example, if 𝑛 can be factored as 𝑛 = × × ⋯ × , then we combine the third and the fourth rule to find
- For very large composite numbers 𝑛, note that in order to calculate 𝜙(𝑛) , 𝑛 must be expressed as a product of primes. In other words, the difficulty of finding 𝜙(𝑛) depends on the difficulty of finding the factorization of 𝑛.
- Example
- What is the value of 𝜙(13) ?
- Because 13 is a prime, 𝜙(13) = 13 − 1 = 12
- What is the value of 𝜙(10) ?
- We can use the third rule: 𝜙(10) = 𝜙(2) × 𝜙(5) = 1 × 4 = 4 (2 and 5 are primes)
- What is the value of 𝜙(240) ?
- We cane write 240 = 2 × 3 × 5:
𝜙(240) = (2 − 2) × (3 − 3) × (5 − 5) = 64
- We cane write 240 = 2 × 3 × 5:
- What is the value of 𝜙(13) ?
- Can we say that 𝜙(49) = 𝜙(7) × 𝜙(7) = 6 × 6 = 36?
→ No, relatively prime(서로소)이 아니기 때문. 𝜙(49) = 𝜙(7) = (7 - 7) = 42
Euler’s Theorem
- Euler’s theorem can be thought of as a generalization of Fermat’s little theorem
- The modulus in the Fermat theorem is a prime, the modulus in Euler’s theorem is an integer.
- First version
- If 𝑎 and 𝑛 are coprime, then 𝑎≡ 1 ( 𝑚𝑜𝑑 𝑛 )
- Second version → Used in the RSA cryptography
- If 𝑛 = 𝑝 × 𝑞, 𝑎 < 𝑛, and 𝑘 is an integer, then 𝑎 ≡ 𝑎 (𝑚𝑜𝑑 𝑛)
- Informal proof of the second version based on the first version
- Because 𝑎 < 𝑛, three cases are possible:
- If 𝑎 is neither a multiple of 𝑝 nor a multiple of 𝑞, then 𝑎 and 𝑛 are coprimes.
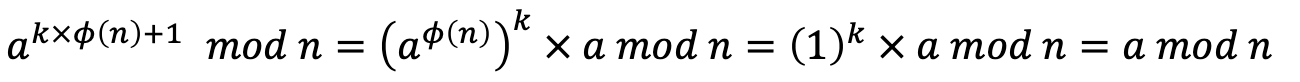
- If 𝑎 is neither a multiple of 𝑝 nor a multiple of 𝑞, then 𝑎 and 𝑛 are coprimes.
- If 𝑎 is a multiple of 𝑝 ( 𝑎 = 𝑖 × 𝑝 ) , but not a multiple of 𝑞
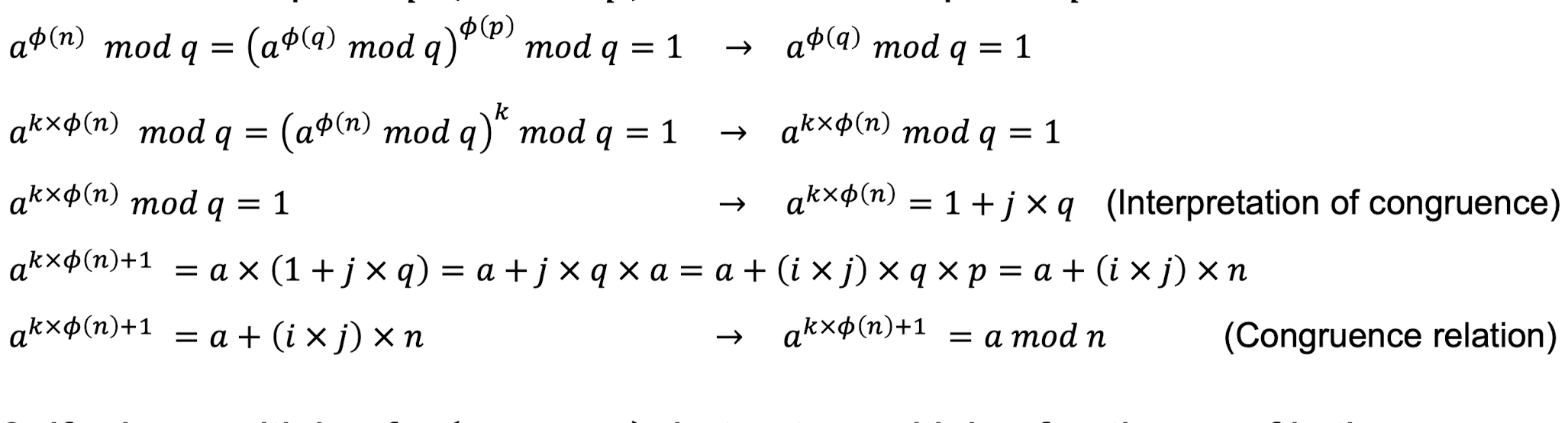
- If 𝑎 is a multiple of 𝑝 ( 𝑎 = 𝑖 × 𝑝 ) , but not a multiple of 𝑞
- If 𝑎 is a multiple of 𝑞 𝑎 = 𝑖 × 𝑞 , but not a multiple of 𝑝, the proof is the same as for the second case, but the roles of 𝑝 and 𝑞 are changed.
- Euler’s theorem sometimes is helpful for quickly finding a solution to some exponentiations.
- Examples


- Euler’s theorem can be used to find multiplicative inverses modulo a prime; Euler’s theorem can be used to find multiplicative inverses modulo a composite.
- If 𝑛 and 𝑎 are coprime, then 𝑎 𝑚𝑜𝑑 𝑛 = 𝑎 𝑚𝑜𝑑 𝑛
- Proof (by multiply both side of the equality by 𝑎)
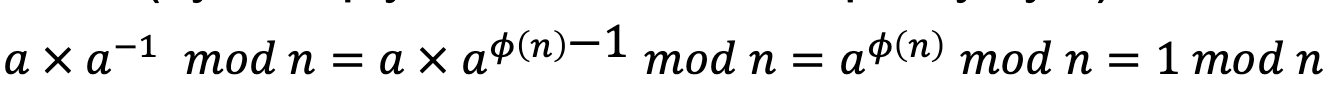
- Proof (by multiply both side of the equality by 𝑎)
- Example

- If 𝑛 and 𝑎 are coprime, then 𝑎 𝑚𝑜𝑑 𝑛 = 𝑎 𝑚𝑜𝑑 𝑛
RSA Algorithm: Another Version
Step 4 in the previous version
→ Select the private key D such that the following equation is true:
(D x E) mod (P – 1) x (Q – 1) = 1
Proof of RSA
- Using the second version of Euler’s theorem
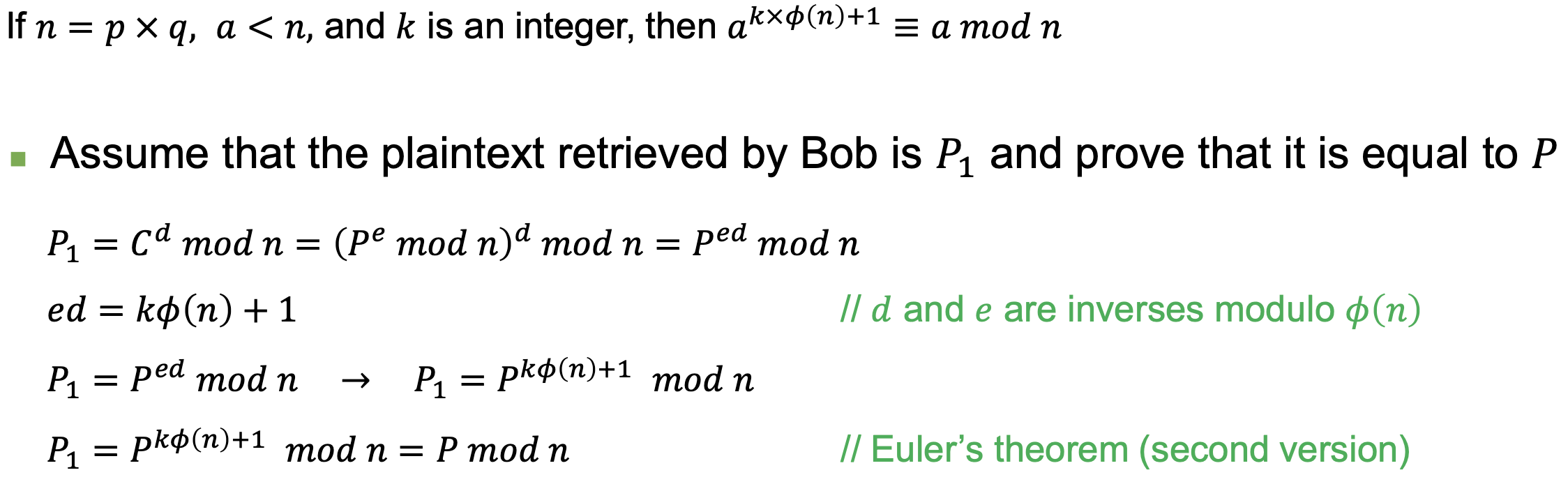
Example
- Jennifer creates a pair of keys for herself. She chooses 𝑝 = 397 and 𝑞 = 401. She calculates 𝑛 = 159197. She then calculates 𝜙(𝑛) = 158400. She then chooses 𝑒 = 343 and 𝑑 = 12007. Show how Ted can send a message to Jennifer if he knows 𝑒 and 𝑛.
- Suppose Ted wants to send the message “NO” to Jennifer.
→ N=13, O=14 (if A=0)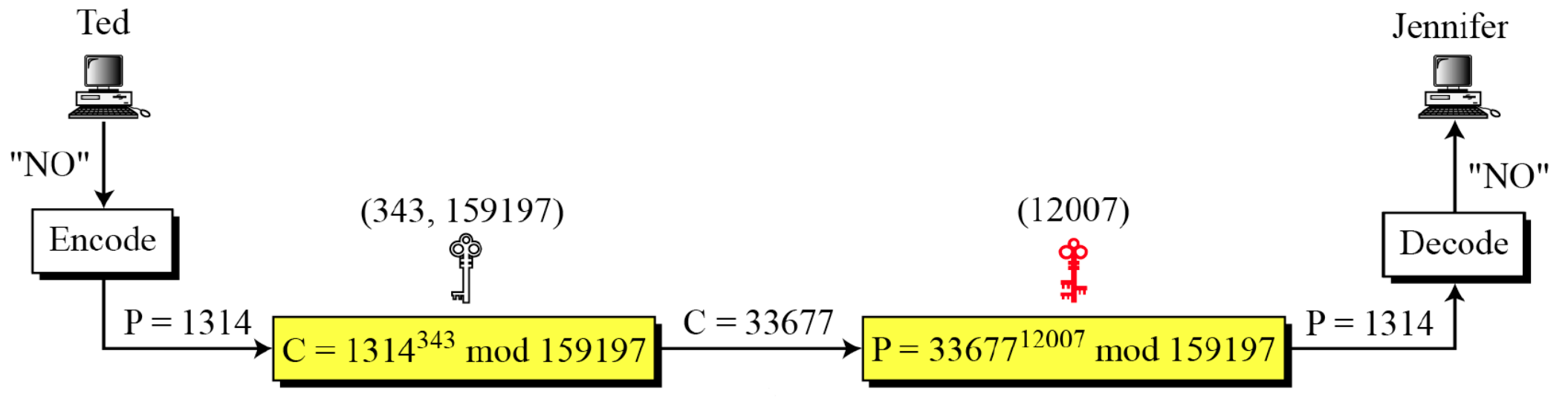
- Suppose Ted wants to send the message “NO” to Jennifer.
ElGamal Cryptography
- 4.5 Elgamal Cryptography → Please read text book
- Elliptic Curve Cryptography
Message Digests
- Message Digest(응축, 압축) Concept
- Also called as Hash
- Unique representation of a message
- Similar to fingerprint of a human
Message Integrity
- In cryptography systems secrecy, or confidentiality is a important goal.
- However, there are occasions where we may not even need secrecy but instead must have integrity.
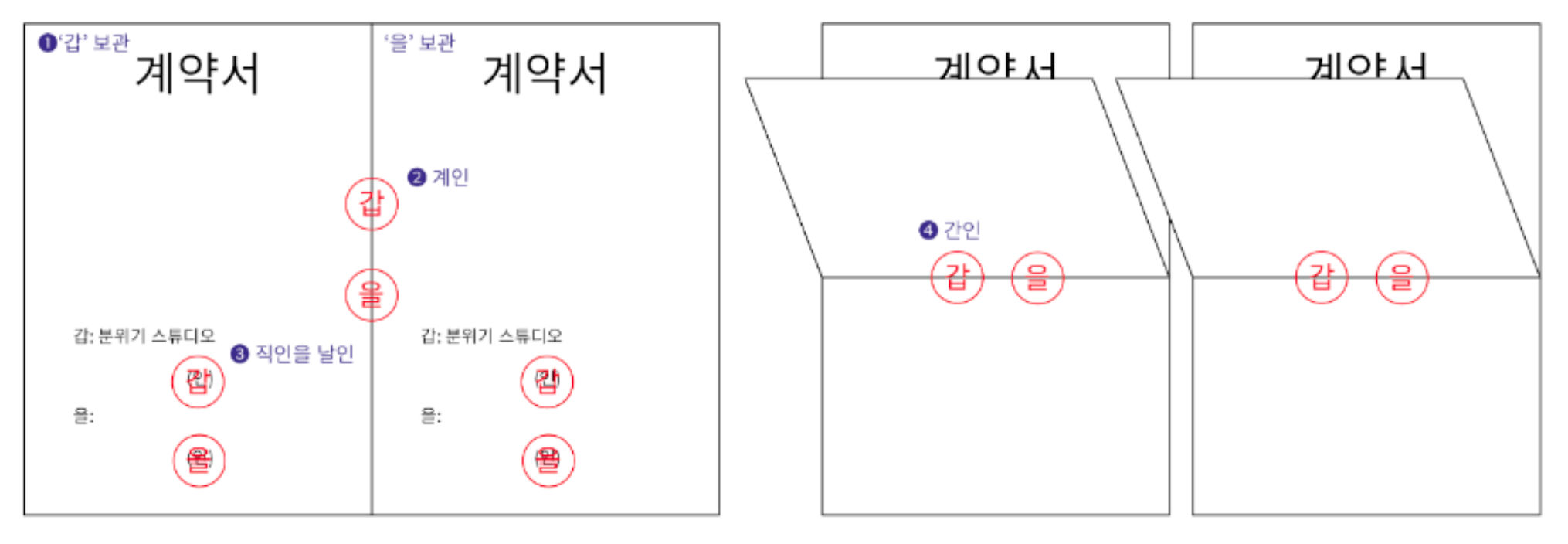
- One way to preserve the integrity of a document is through the use of a fingerprint.
- If Alice needs to be sure that the contents of her document will not be changed, she can put her fingerprint at the bottom of the document.
→ 메세지 변조 없이
- If Alice needs to be sure that the contents of her document will not be changed, she can put her fingerprint at the bottom of the document.
- 직인 날인, 계인, 간인
Message and Message Digest
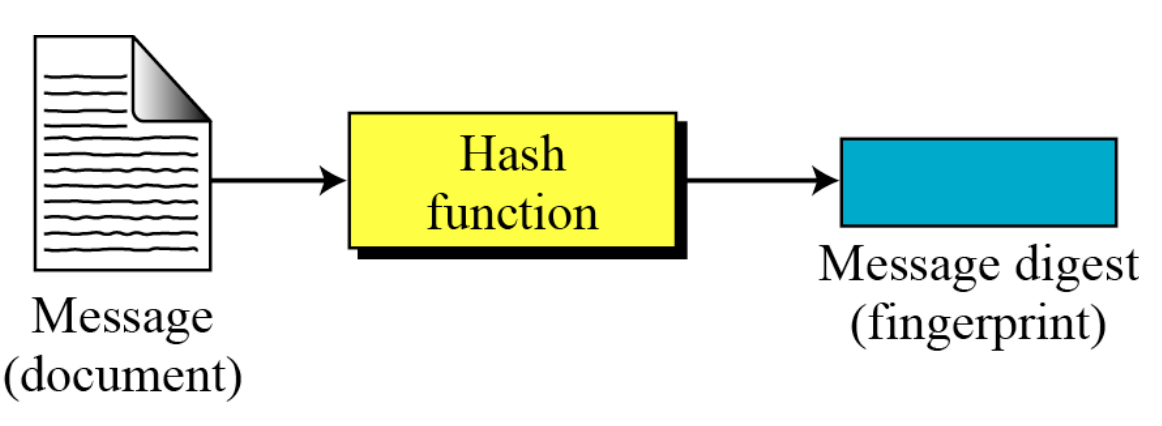
- The electronic equivalent of the document and fingerprint pair is the message and digest pair.
- To preserve the integrity of a message, the message is passed through an algorithm called a cryptographic hash function
- The function creates a compressed image of the message that can be used like a fingerprint.
- The two pairs (document / fingerprint) and (message / message digest) are similar, with some differences.
- The document and fingerprint are physically linked together
- The message and message digest can be unlinked (or sent) separately.
- Most importantly, the message digest needs to be safe from change.
Idea of Message Digest
- Simplistic example of message digest
- Multiply each digit in the number with the next digit (excluding it if its 0)
- Disregarding the first digit of the multiplication operation, if the result is a two- digit number

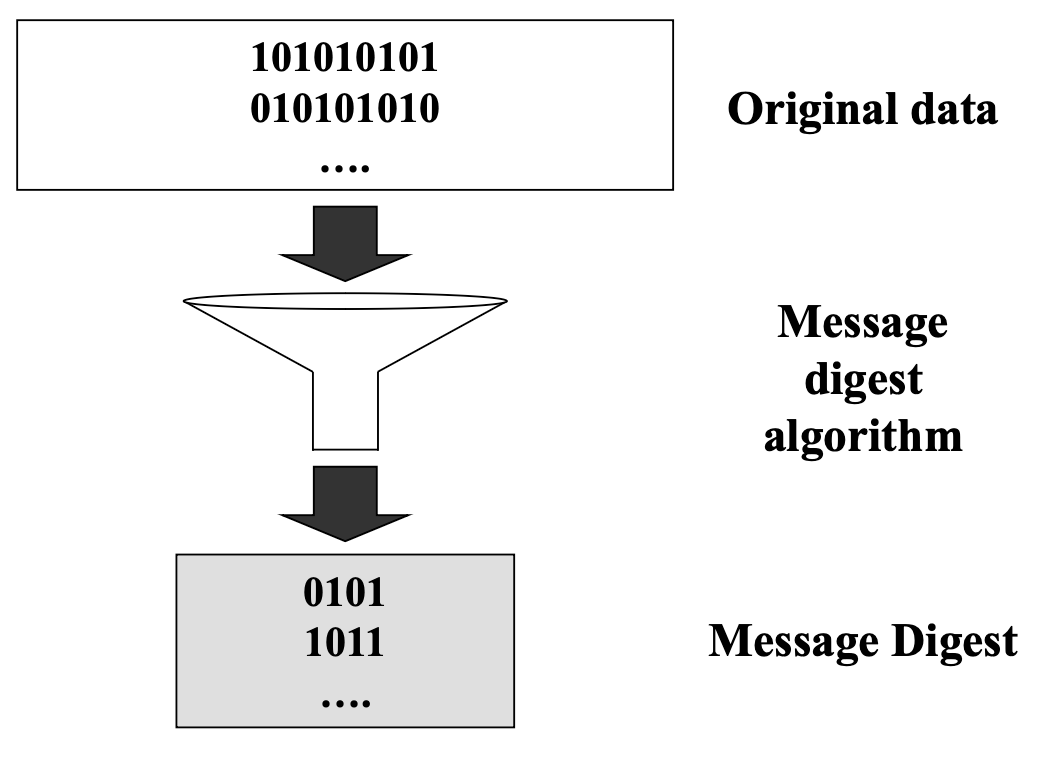
- We perform a hashing operation (or a message digest algorithm) over a block of data to produce its hash or message digest, which is smaller in size that the original message
Requirements of a Message Digest
- Given a message, it should be very easy to find its corresponding message digest and the message digest must always be the same
- Given a message digest, it should be very difficult to find the original message for which the digest was created
- Given any two messages, if we calculate their message digests, the two message digests must be different → msg 같은건 제외
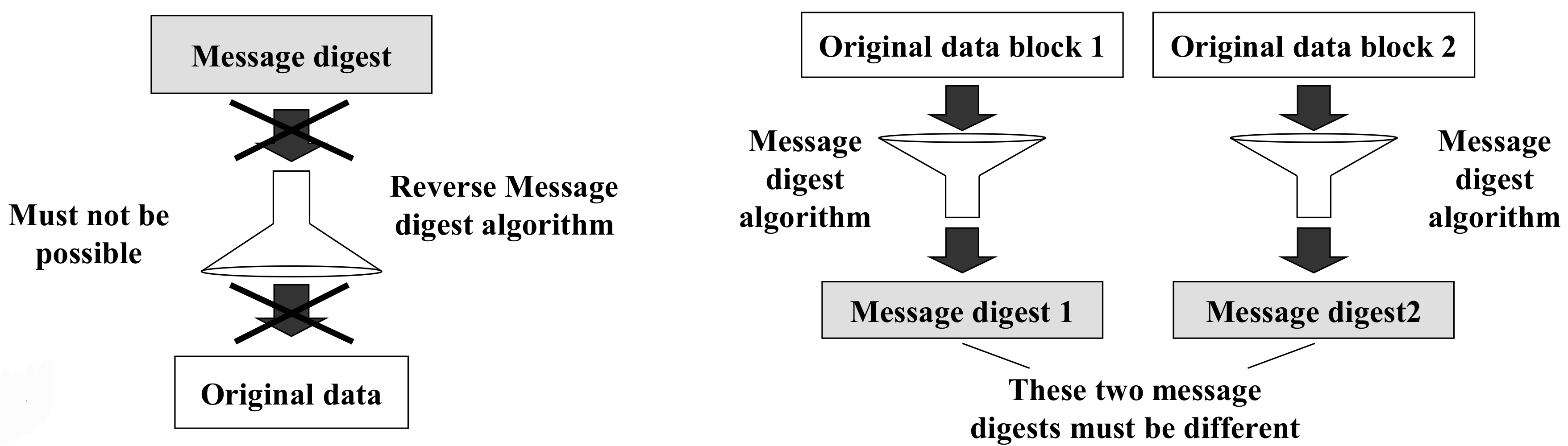
Message Digest Differences
- Even if the original messages differ minutely, message digests differ dramatically
- Basis for the guarantee of uniqueness

Hash Functions
- Condenses arbitrary message to fixed size
- h = H(M)
- No secret key for input
- Usually assume hash function is public
- Want a cryptographic hash function
- Computationally infeasible to find data mapping to specific hash (one-way property)
- Computationally infeasible to find two data to same hash (collision-free property)
Hash Function Requirements
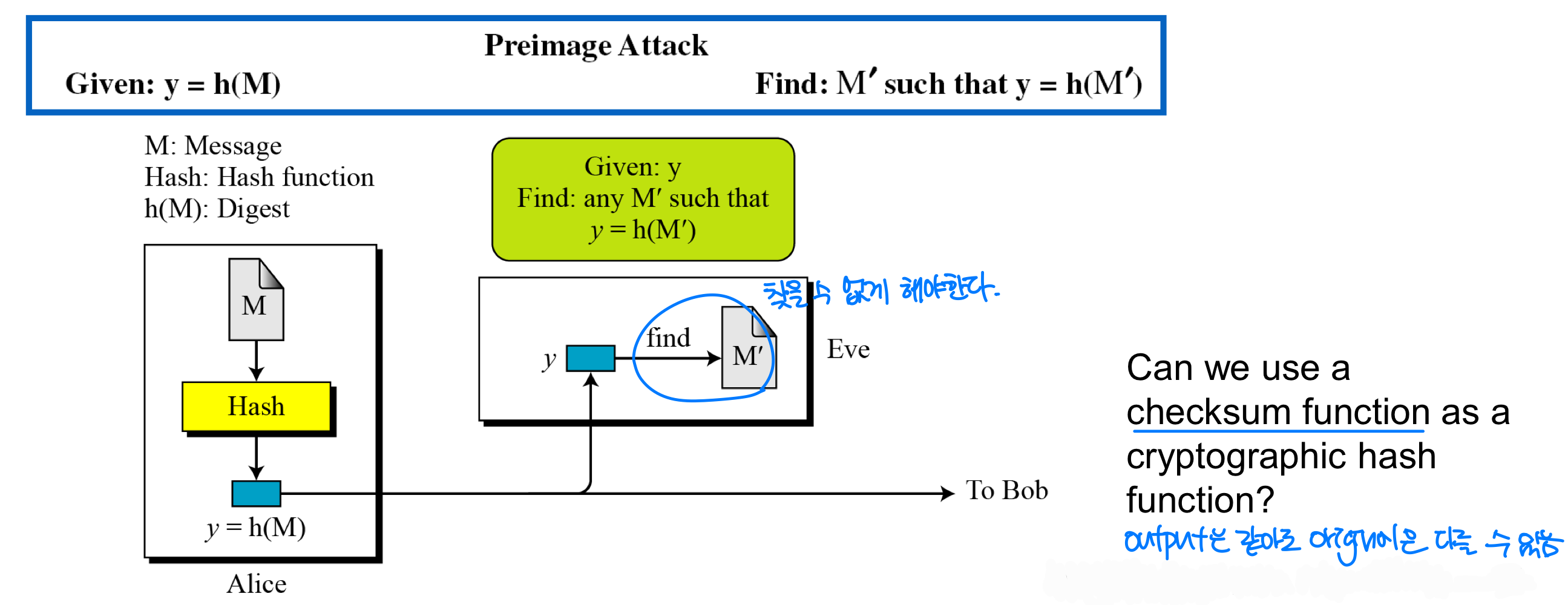
⭐️ Preimage Resistance
- Eve intercepts the digest h(M) and create a message M’.
- Then Eve can send M’ to Bob pretending it is M.
- If M is computed, secret value that is included in M can be easily recovered.
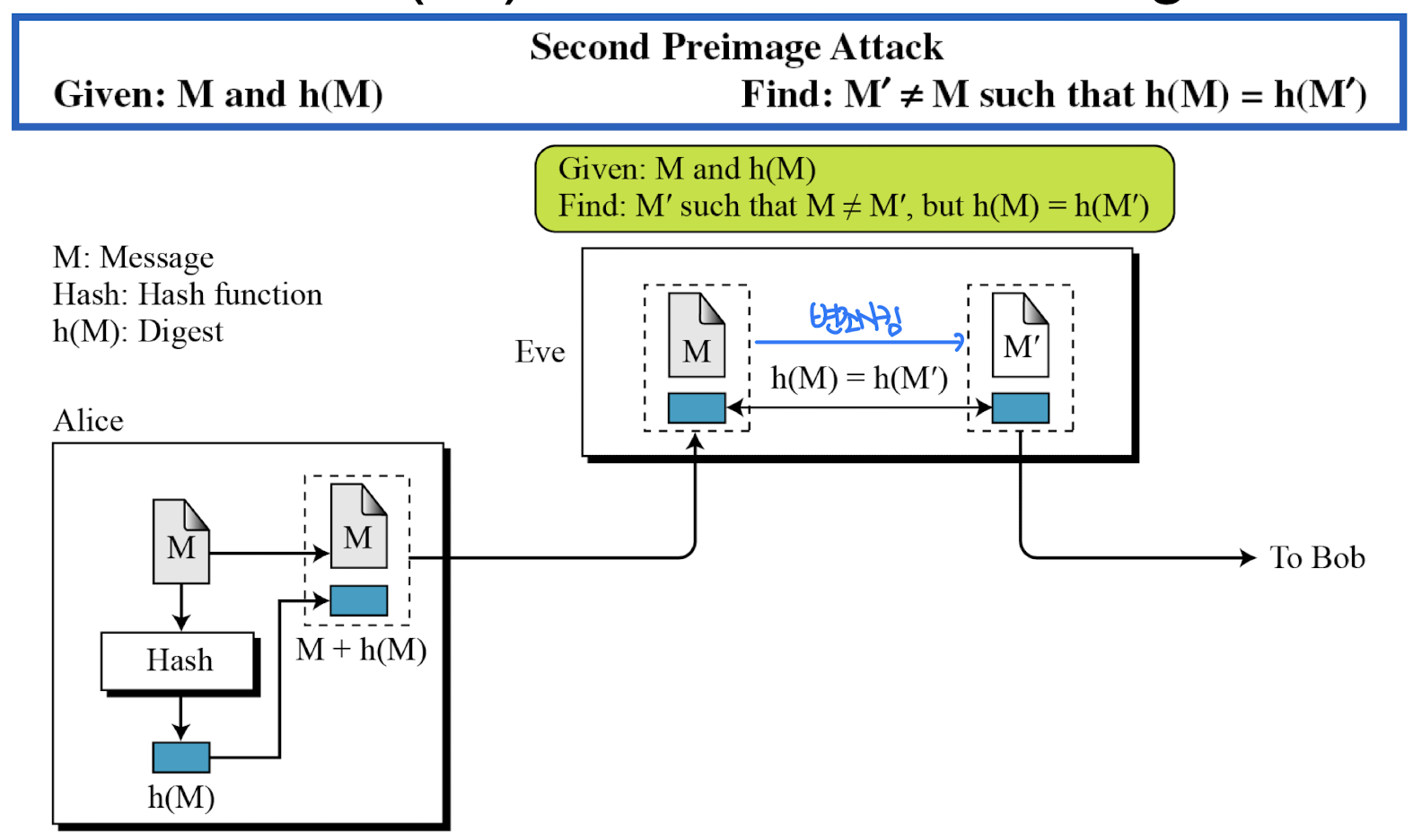
⭐️ Second Preimage Resistance
- Eve intercepts a message M and its digest h(M).
- She creates another message M’ ≠ M, but h(M) = h(M’).
- Eve sends the M’ and h(M’) to Bob. Eve has forged the message
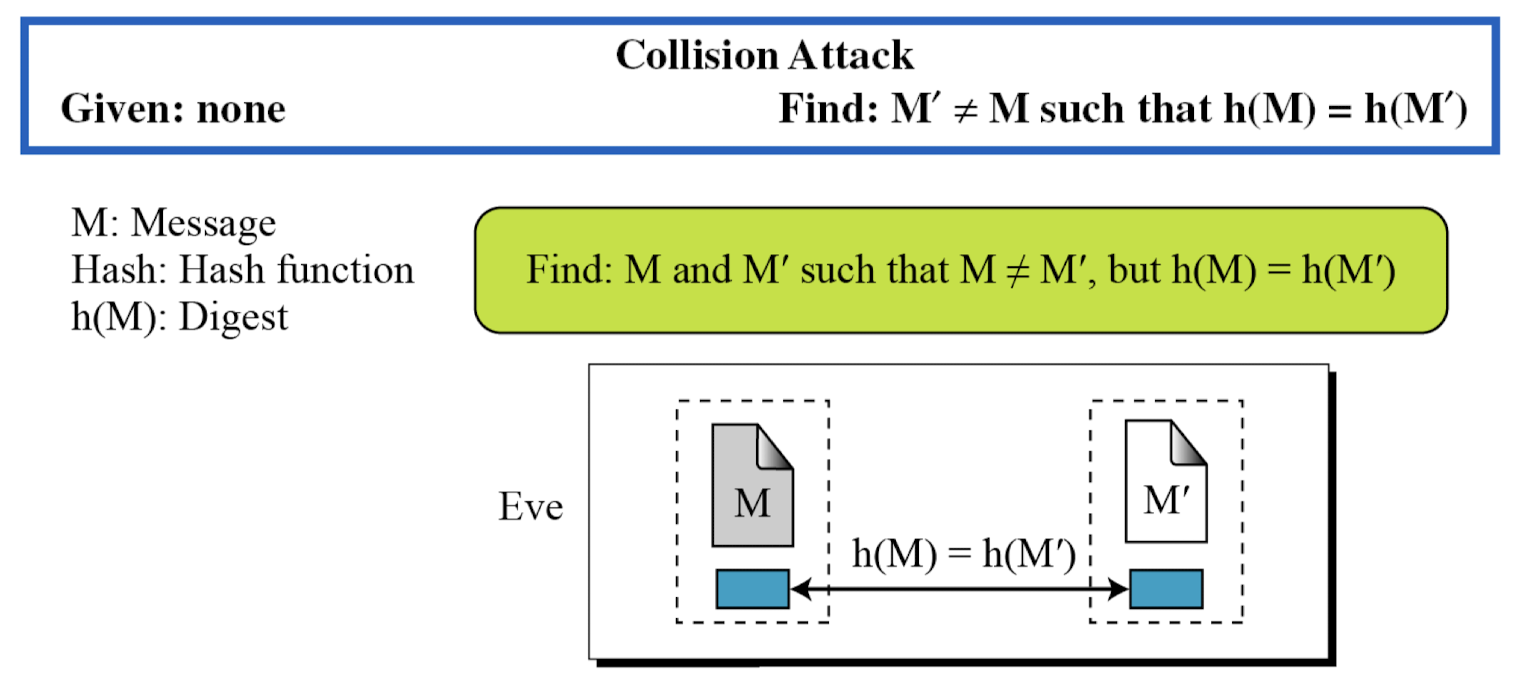
⭐️ Collision Resistance
- Eve cannot find two messages that hash to the same digest
- Here the adversary can create two messages (out of scratch) and hashed to the same digest.
- Two different wills(유언장) can be created that hash to the same digest. When the time comes for the execution of the will, the second (forged) will is presented to the heirs. Because the digest matches both wills, the substitution is undetected
Attacks on Hash Functions
- Have brute-force attacks and cryptanalysis
- A preimage or second preimage attack
- Find y s.t. H(y) equals a given hash value
- Collision resistance
- Find two messages x & y with same hash so H(x) = H(y)
- Hence value 2 determines strength of hash code against brute-force attacks
- 128-bits inadequate, 160-bits suspect
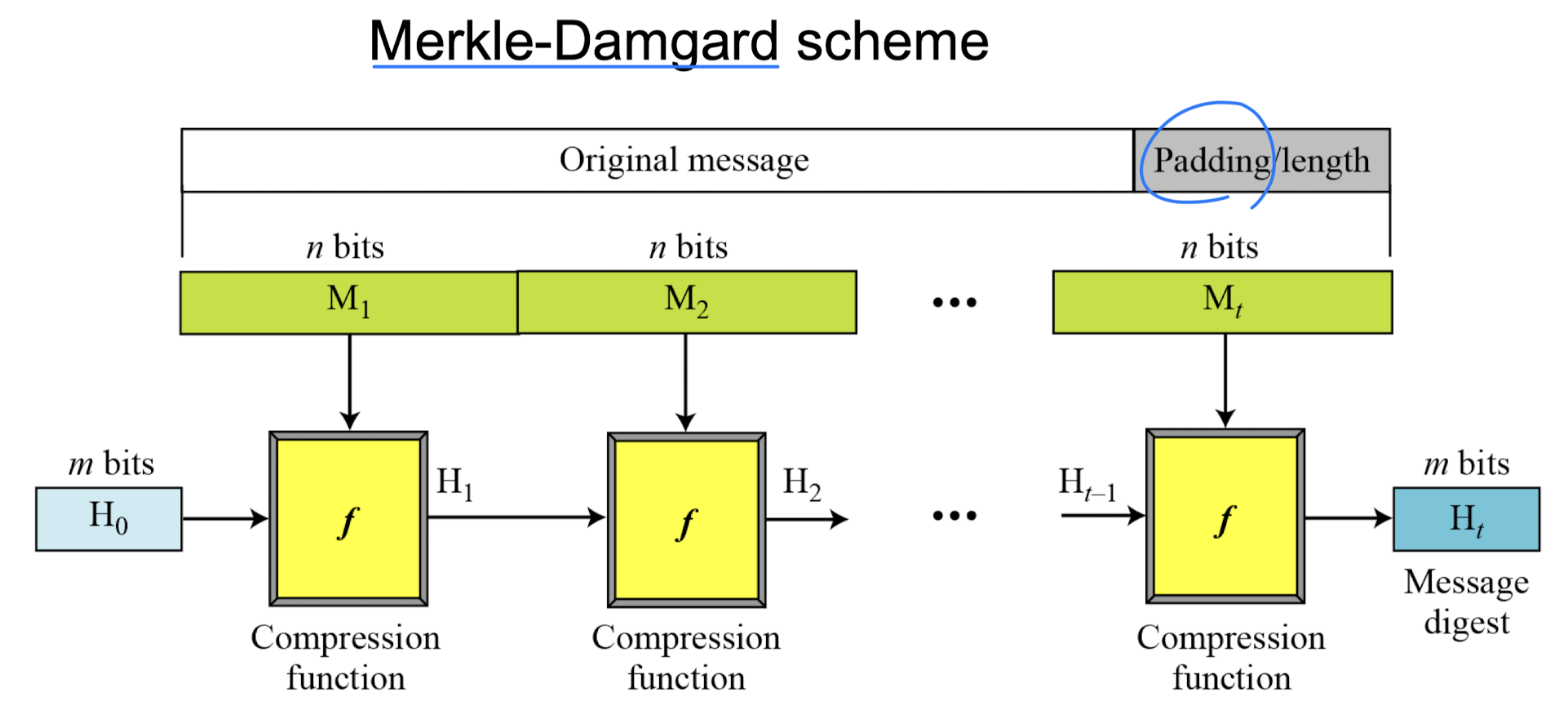
Iterated Hash Function
- A cryptographic hash function takes a message of arbitrary length
and creates a message digest of fixed length. - Creating such a function is best accomplished using iteration.
- Instead of using a hash function with variable-size input, a function with fixed size input is created and used a necessary number of times
- Merkle-Damgard Scheme
Two Groups of Compression Functions
- Hash functions made from scratch
- Message Digest (MD)
- SHA
- Hash functions based on block ciphers
- Rabin scheme
- Whirlpool → AES
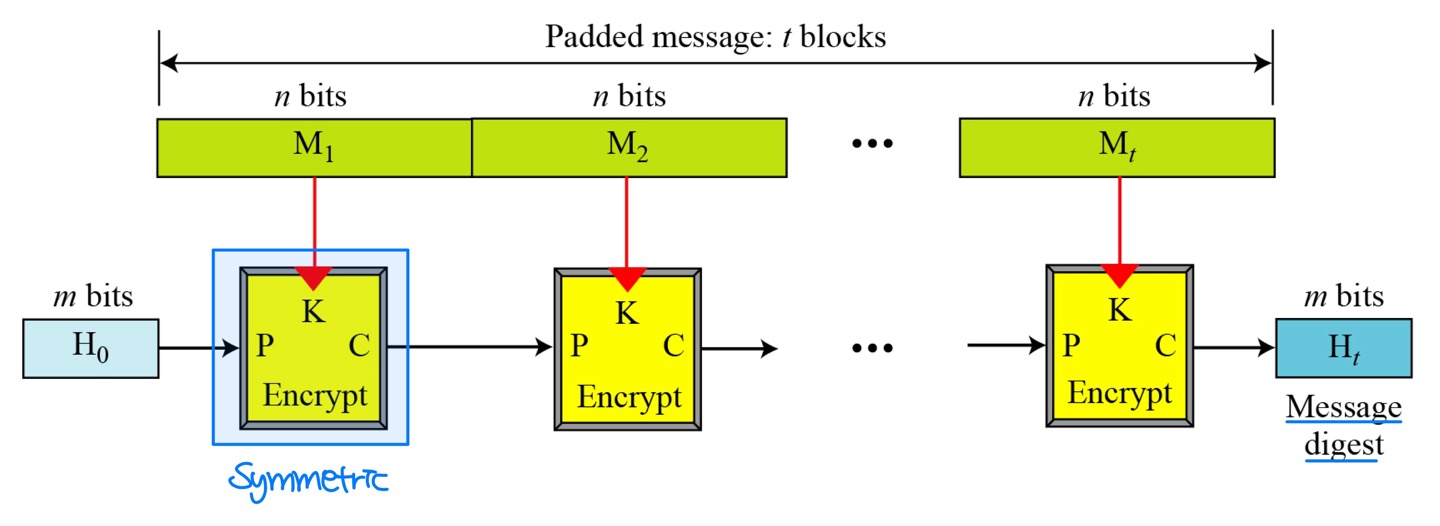
Rabin Scheme
- Rabin scheme is based on the Merkle-Damgard scheme.
- The compression function is replaced by any encrypting cipher.
- The message block is used as the key; the previously created digest is used as the plaintext. The ciphertext is the new message digest
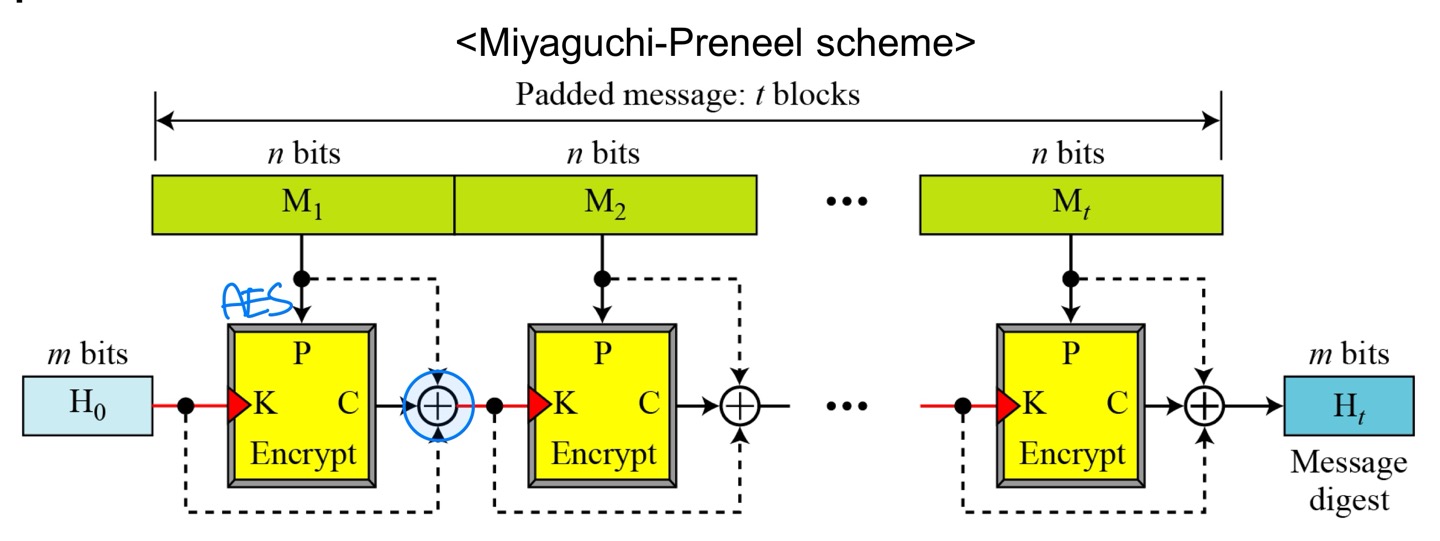
Whirlpool
- Whirlpool is an iterated cryptographic hash function, based on the
Miyaguchi-Preneel scheme, that uses a symmetric-key block cipher in place of the compression function. - The block cipher is a modified AES cipher that has been tailored for this purpose.
Secure Hash Algorithm
- SHA originally designed by NIST & NSA in 1993
- Was revised in 1995 as SHA-1
- US standard for use with DSA signature scheme
- standard is FIPS 180-1 1995, also Internet RFC3174
- the algorithm is SHA, the standard is SHS
- Based on design of MD4 with key differences
- Produces 160-bit hash values
- Recent 2005 results on security of SHA-1 have raised concerns on its use in future applications
Revised Secure Hash Standard
- NIST issued revision FIPS 180-2 in 2002
- Adds 3 additional versions of SHA
- SHA-256, SHA-384, SHA-512
- Designed for compatibility with increased security provided by the AES cipher
- Structure & detail is similar to SHA-1
- Hence analysis should be similar
- But security levels are rather higher
SHA Versions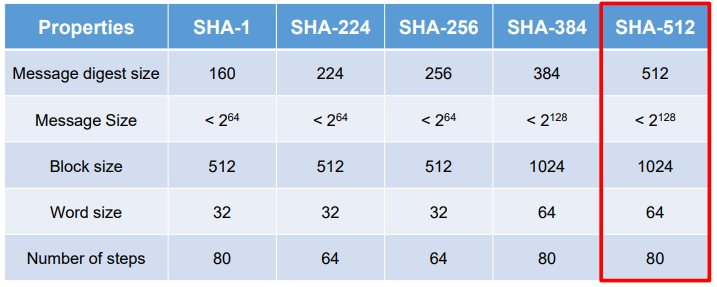
SHA-512
- Overview
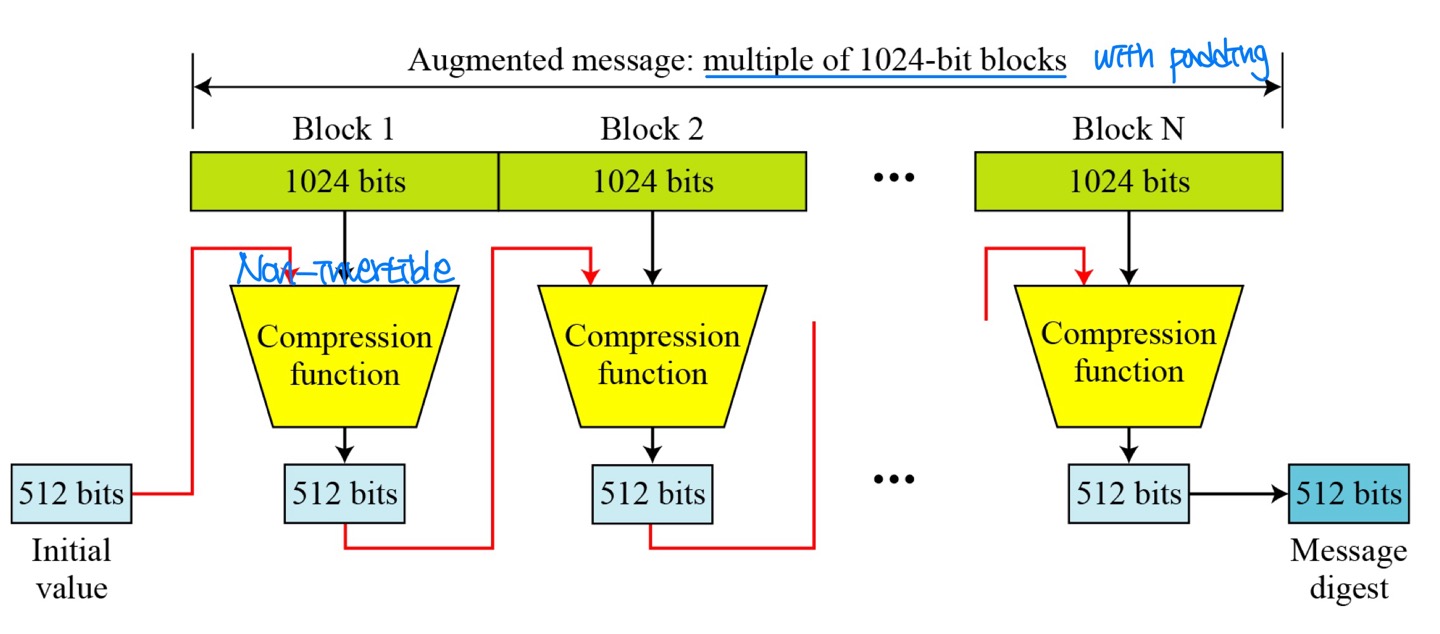 → Invertibility 필요 X / Inverse 과정 필요 X
→ Invertibility 필요 X / Inverse 과정 필요 X
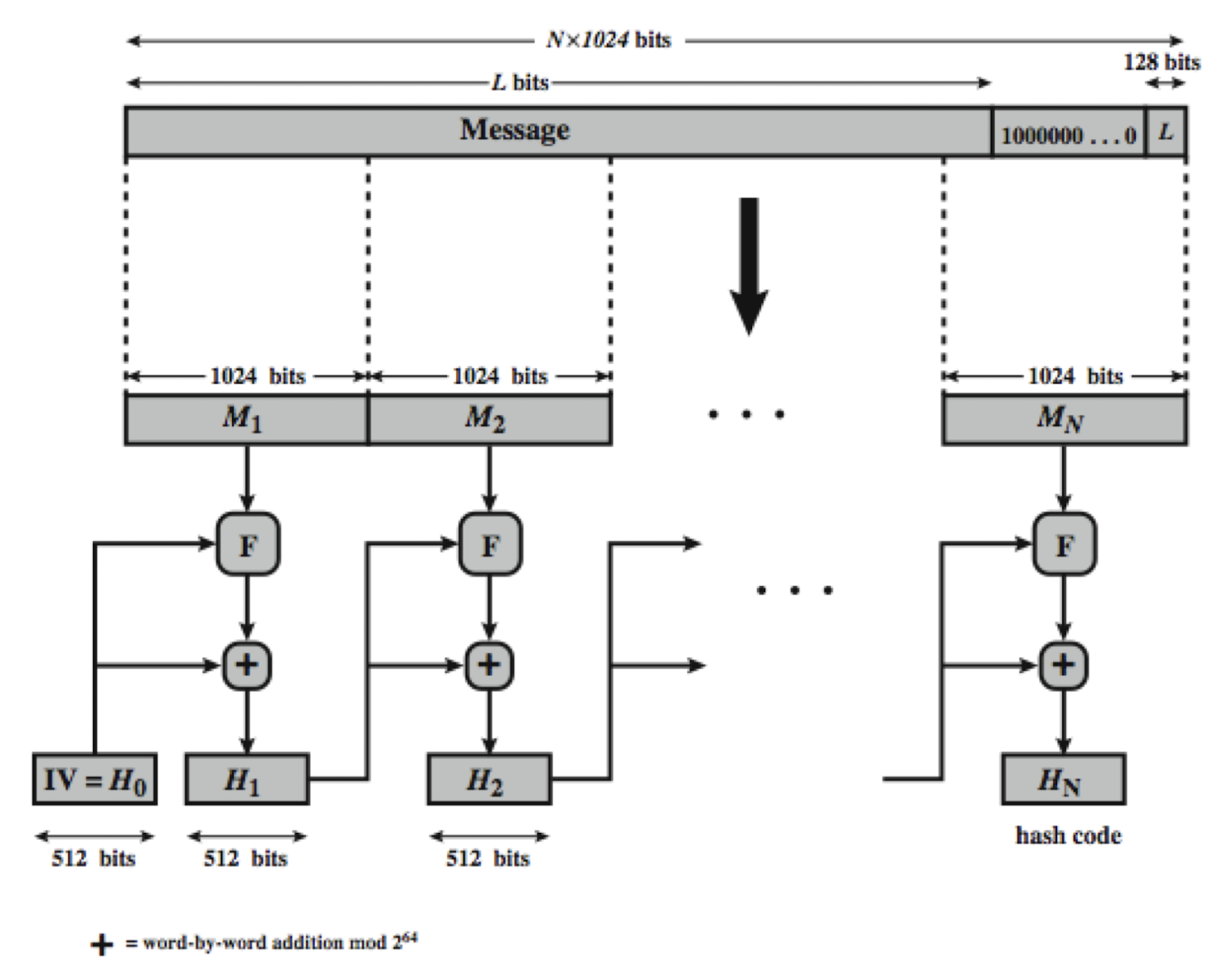
- Message preparation
- SHA-512 insists that the length of the original message be less than 2 bits.
- SHA-512 creates a 512-bit message digest out of a message less than 2
- Example: The message length limitation of SHA-512 is not a serious problem. Suppose we need to send a message that is 2 bits in length. How long does it take for a communications network with a data rate of 2 bits per second to send this message?
- Solution: A communications network that can send 2 bits per second is not yet available. Even if it were, it would take many years to send this message. This tells us that we do not need to worry about the SHA-512 message length restriction.
- Example: The message length limitation of SHA-512 is not a serious problem. Suppose we need to send a message that is 2 bits in length. How long does it take for a communications network with a data rate of 2 bits per second to send this message?
- Step 1 & 2: Length field and padding

- Example: What is the number of padding bits if the length of the original message is 2590 bits?
- 354 bits
- Example: What is the minimum and maximum number of padding bits that can be added to a message?
Solution → 읽어보기- The minimum length of padding is 0 and it happens when (−M − 128) mod 1024 is 0. This means that |M| = −128 mod 1024 = 896 mod 1024 bits. In other words, the last block in the original message is 896 bits. We add a 128-bit length field to make the block complete.
- The maximum length of padding is 1023 and it happens when (−|M| −128) = 1023 mod 1024. This means that the length of the original message is |M| = (−128 −1023) mod 1024 or the length is |M| = 897 mod 1024. In this case, we cannot just add the length field because the length of the last block exceeds one bit more than 1024. So we need to add 897 bits to complete this block and create a second block of 896 bits. Now the length can be added to make this block complete.
- Example: What is the number of padding bits if the length of the original message is 2590 bits?
- Step 3: Dividing the input into 1024-bit blocks
- A message block and the digest as words
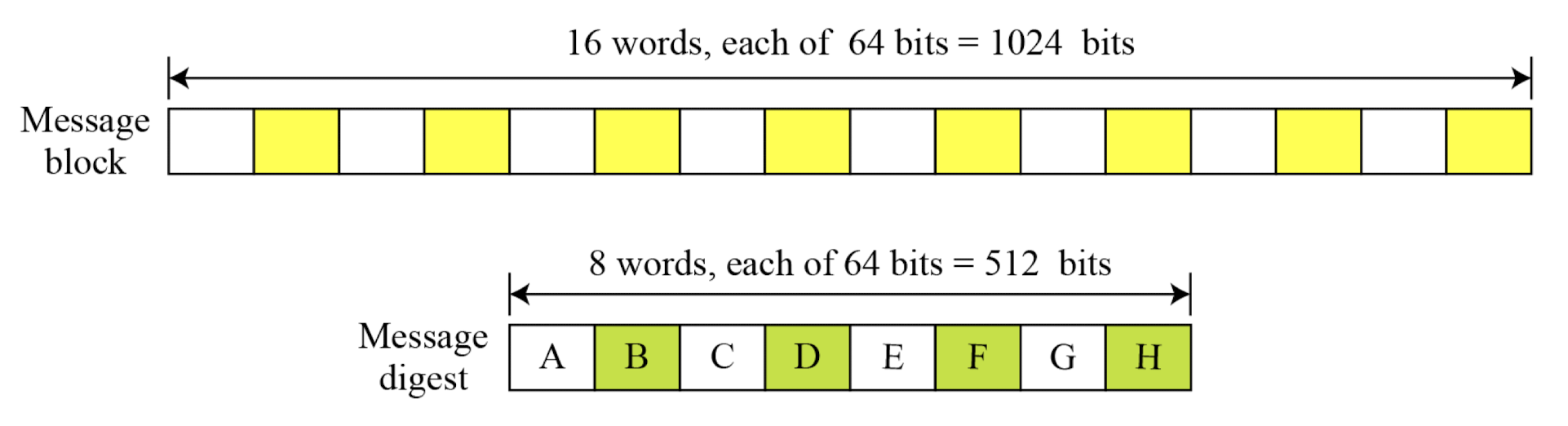
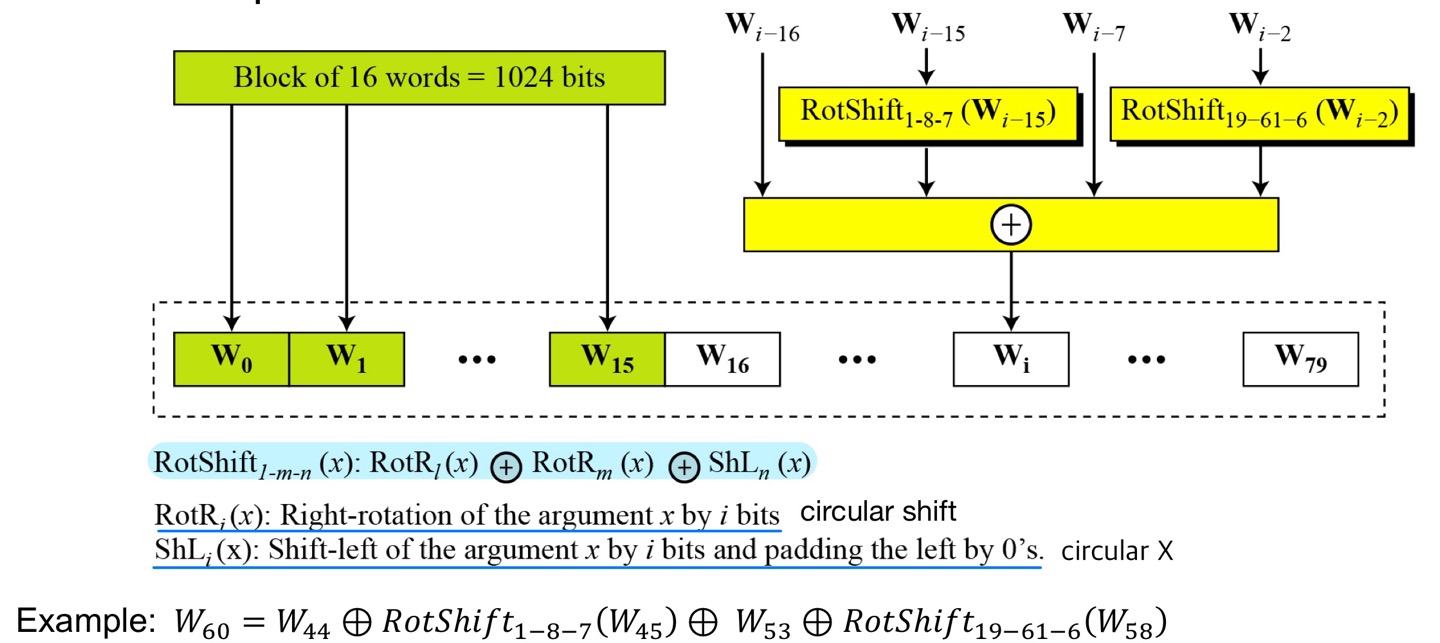
- Words expansion in SHA-512
- A message block and the digest as words
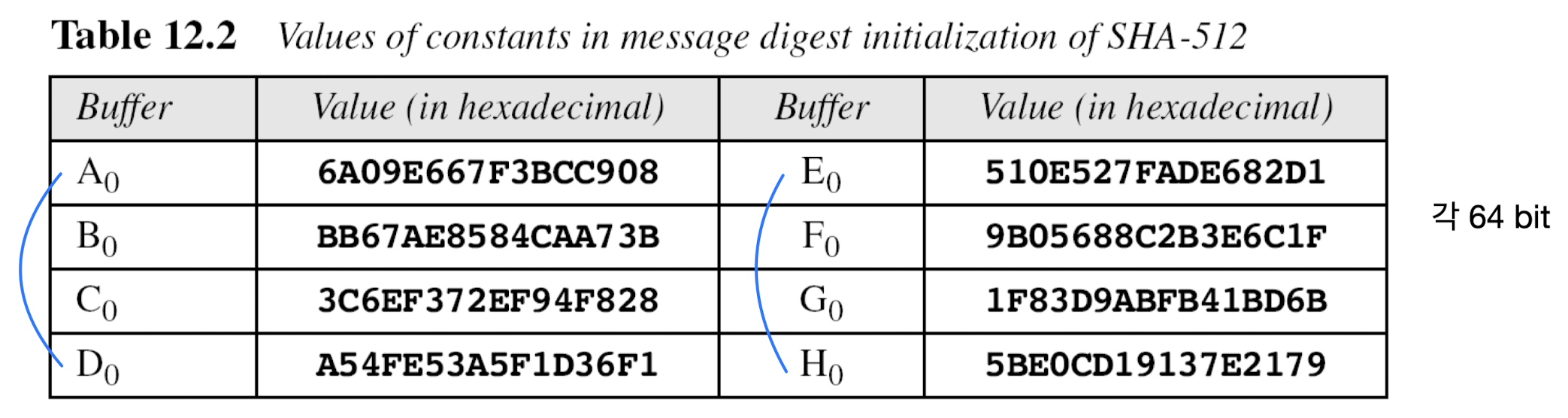
- Step 4: Initialize chaining variables
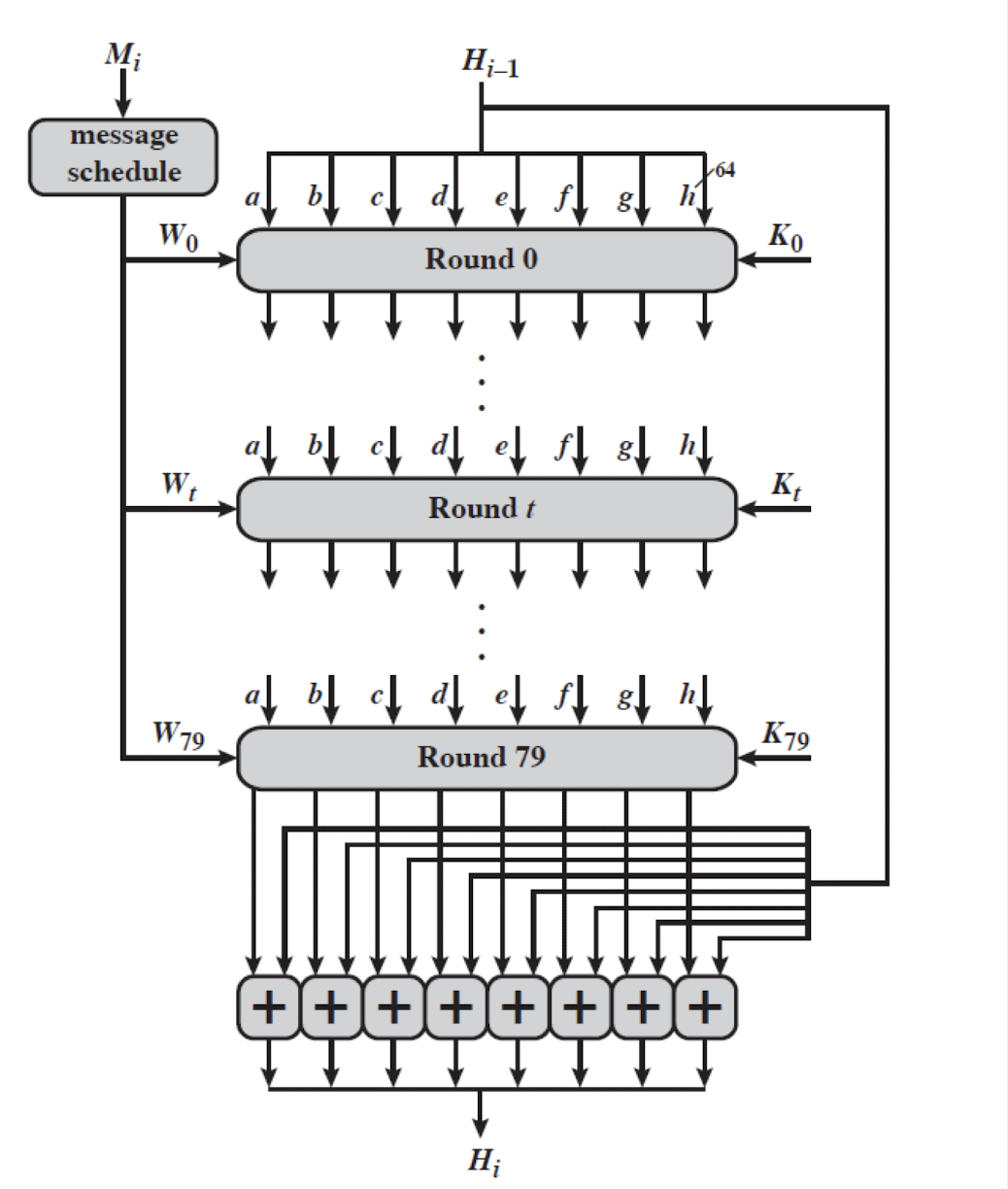
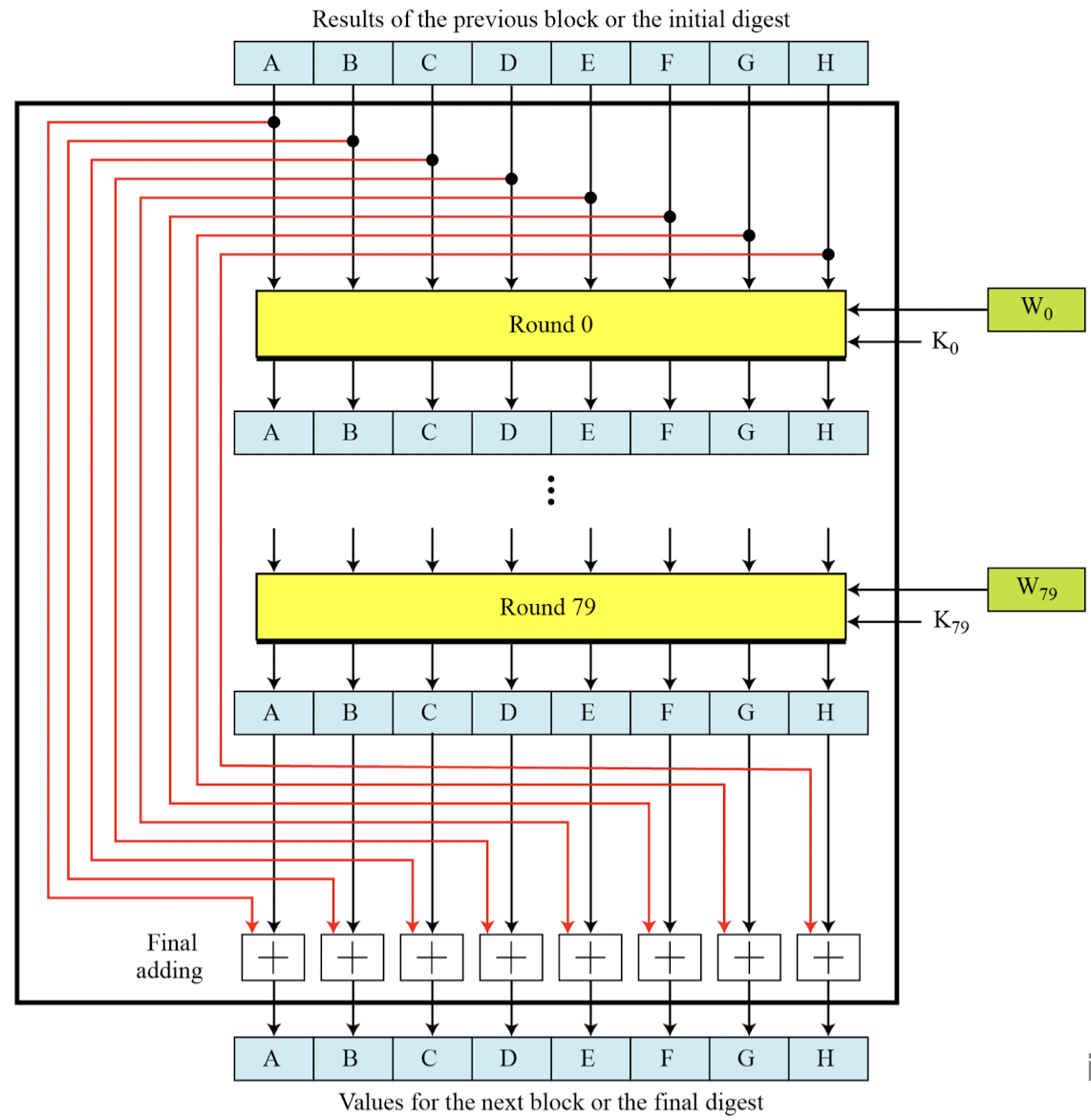
- Step 5: ⭐️ Compression function
- Heart of the algorithm
- Processing message in 1024-bit blocks
- Consists of 80 rounds
- Updating a 512-bit buffer
- Using a 64-bit value 𝑊 derived from the current message block
- A round constant based on cube root of first 80 prime numbers
- Structure of each round in SHA-512
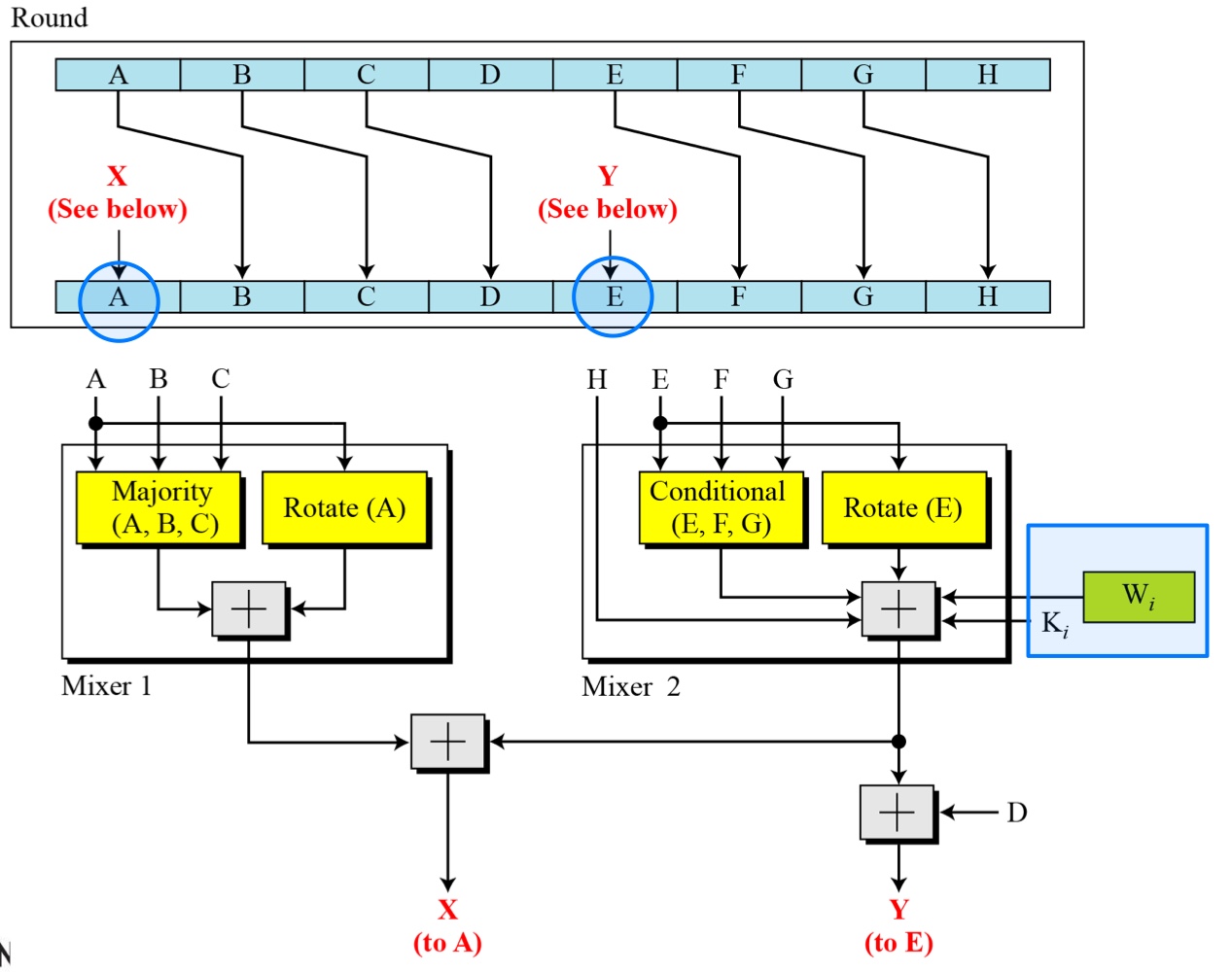
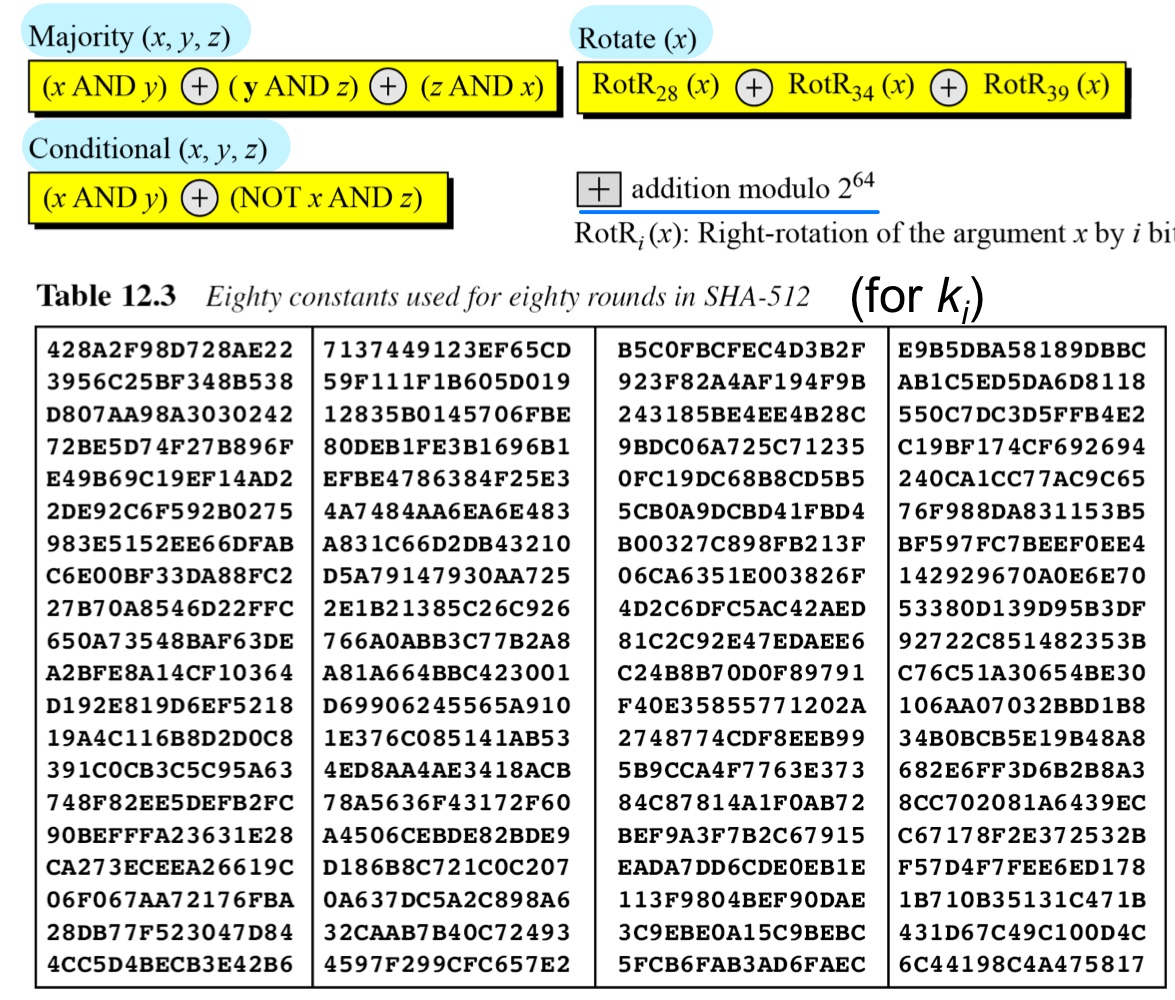
- Example: We apply the Majority function on buffers A, B, and C. If the leftmost hexadecimal digits of these buffers are 0x7, 0xA, and 0xE, respectively, what is the leftmost digit of the result?
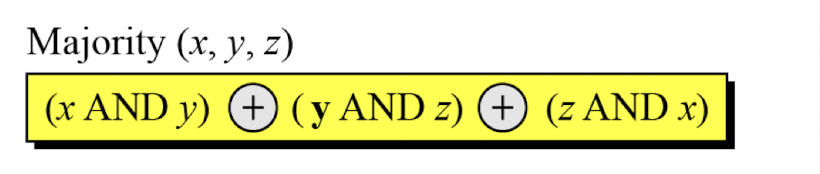
- Solution: The digits in binary are 0111, 1010, and 1110

- Solution: The digits in binary are 0111, 1010, and 1110
- Example: We apply the Conditional function on E, F, and G buffers. If the leftmost hexadecimal digits of these buffers are 0x9, 0xA, and 0xF respectively, what is the leftmost digit of the result?
- Solution: The digits in binary are 1001, 1010, and 1111.

- Solution: The digits in binary are 1001, 1010, and 1111.
Analysis
- With a message digest of 512 bits, SHA-512 expected to be resistant to all attacks, including collision attacks.
Message Authentication Code (MAC)
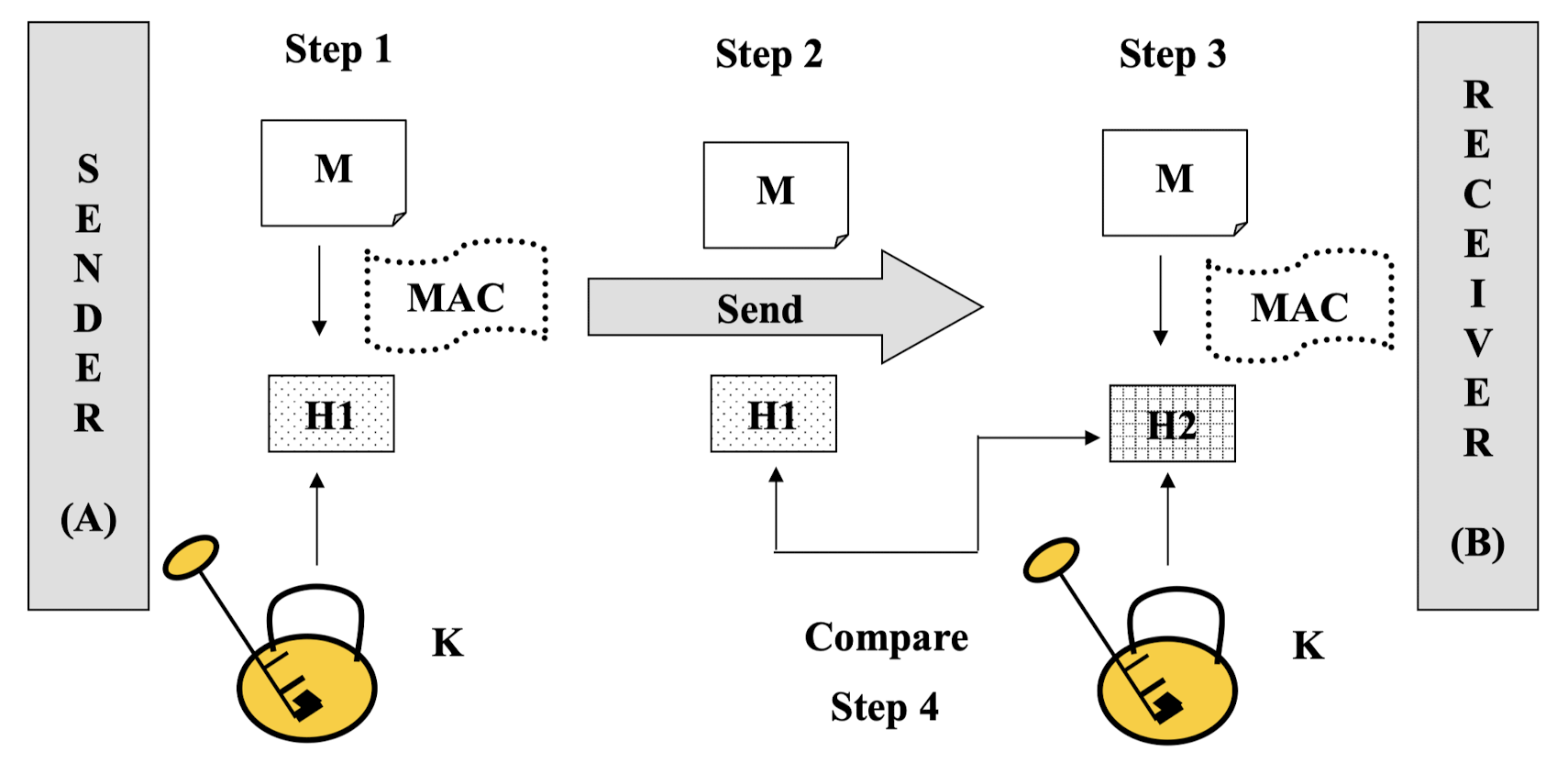
- Message Authentication Code (MAC)
- Similar to message digest
- In addition, also involves encryption and decryption
- Sender and receiver must know a shared secret key
Message Authentication
- Message authentication is concerned with:
- Protecting the integrity of a message
- Validating identity of originator
- Message authentication is against active attack such as message modification.
- We may also want to verify a message’s timeliness – no delay, no replay.
- Symmetric encryption alone is not a suitable tool for data authentication.
- Example) reordering in ECB
- Message authentication without confidentiality
- Broadcast message
- Example) network unavailable message
- One side has heavy load and cannot afford the time to decrypt all incoming messages
- Authentication of computer program in plaintext
- Broadcast message
- A message digest does not authenticate the sender of the message.
- To provide message authentication, Alice needs to provide proof that it is Alice sending the message and not an impostor.
- The digest created by a cryptographic hash function is normally called a modification detection code (MDC).
- What we need for message authentication is a message authentication code (MAC).
Modification Detection Code (MDC)
- A modification detection code (MDC) is a message digest that can prove the integrity of the message: that message has not been changed.
- If Alice needs to send a message to Bob and be sure that the message will not change during transmission, Alice can create a message digest, MDC, and send both the message and the MDC to Bob. Bob can create a new MDC from the message and compare the received MDC and the new MDC. If they are the same, the message has not been changed
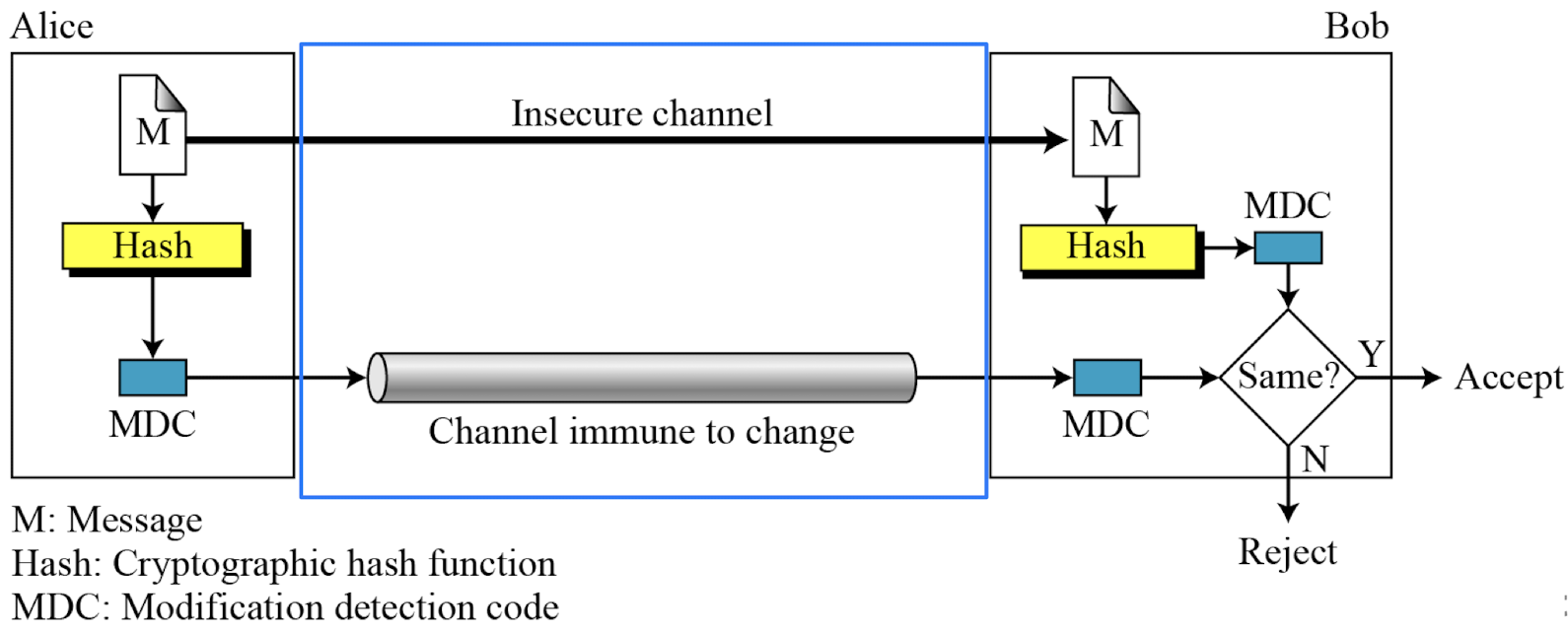
- If Alice needs to send a message to Bob and be sure that the message will not change during transmission, Alice can create a message digest, MDC, and send both the message and the MDC to Bob. Bob can create a new MDC from the message and compare the received MDC and the new MDC. If they are the same, the message has not been changed
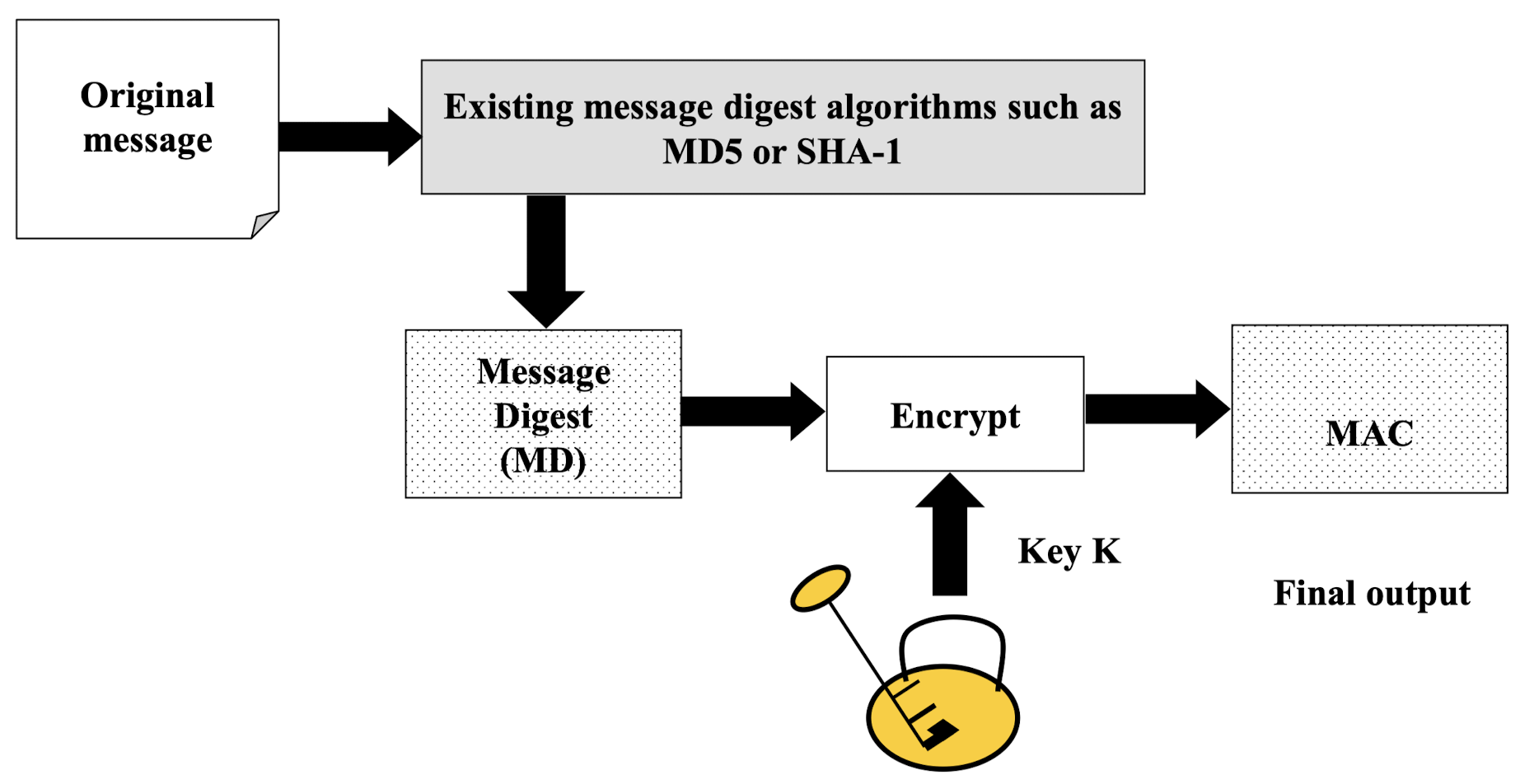
Message Authentication Code (MAC)
- To ensure the integrity of the message and the data origin authentication – that Alice is the originator of the message, not anybody else – we need to change an MDC to a MAC.
- The difference between an MDC and a MAC is that MAC includes a secret between Alice and Bob.
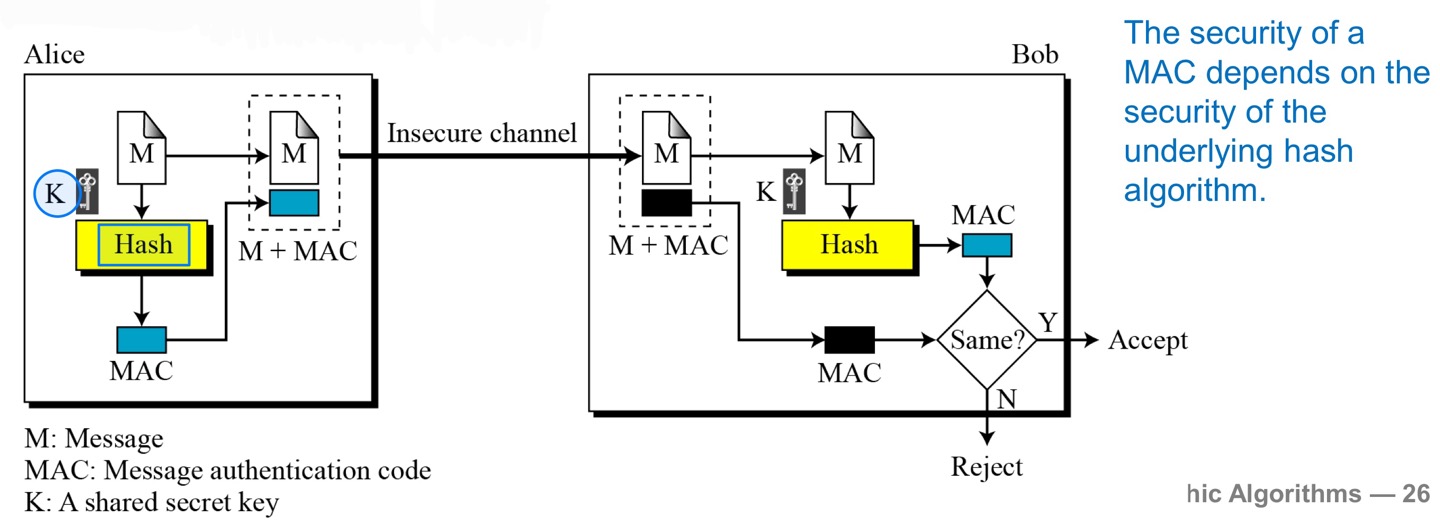 → 이정도는 외우기 (이해하기)
→ 이정도는 외우기 (이해하기)
- The receiver is assured that the message is not modified.
- The receiver is assured that the message is from the sender.
- If the message includes a sequence number, the receiver is assured of proper sequence number.
- Authentication algorithm need not be reversible.
(which is different form encryption alg.)
Message Authentication
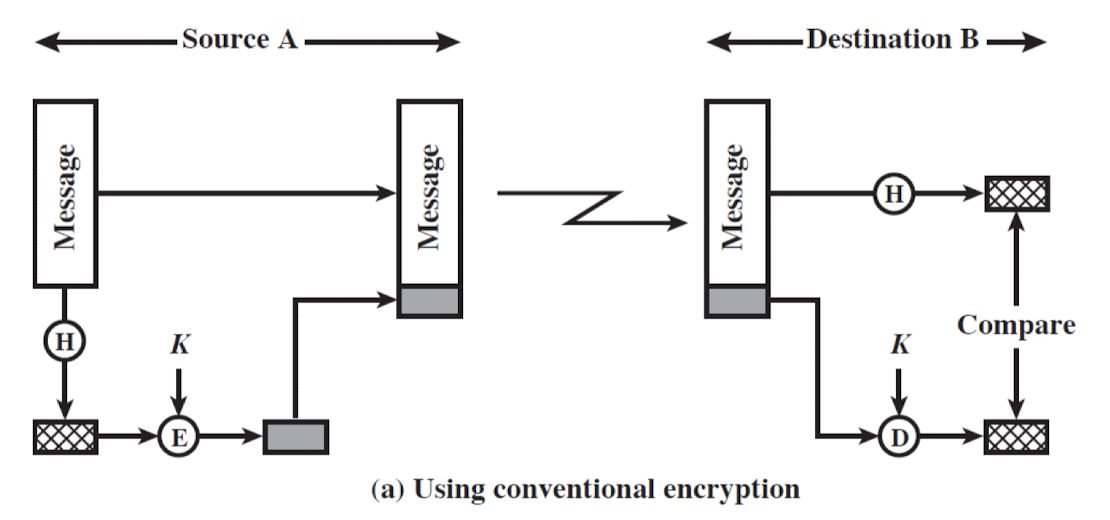
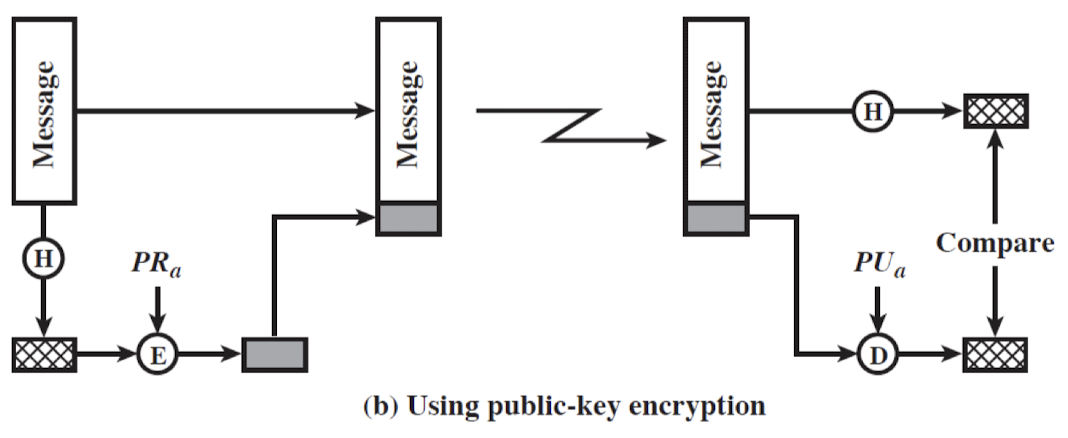
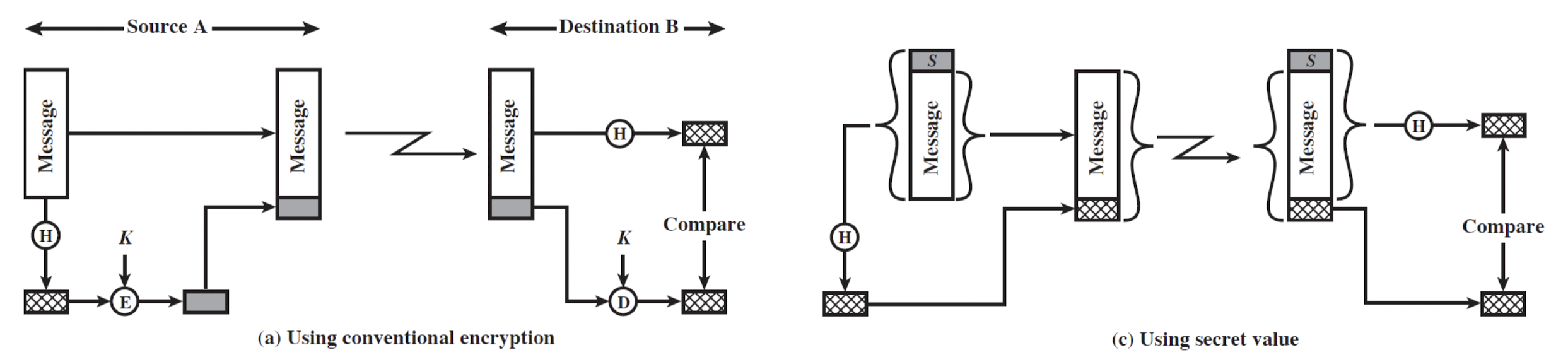
- Three ways in which the message is authenticated:
- Using conventional encryption
- Using public-key encryption
- Using secret value
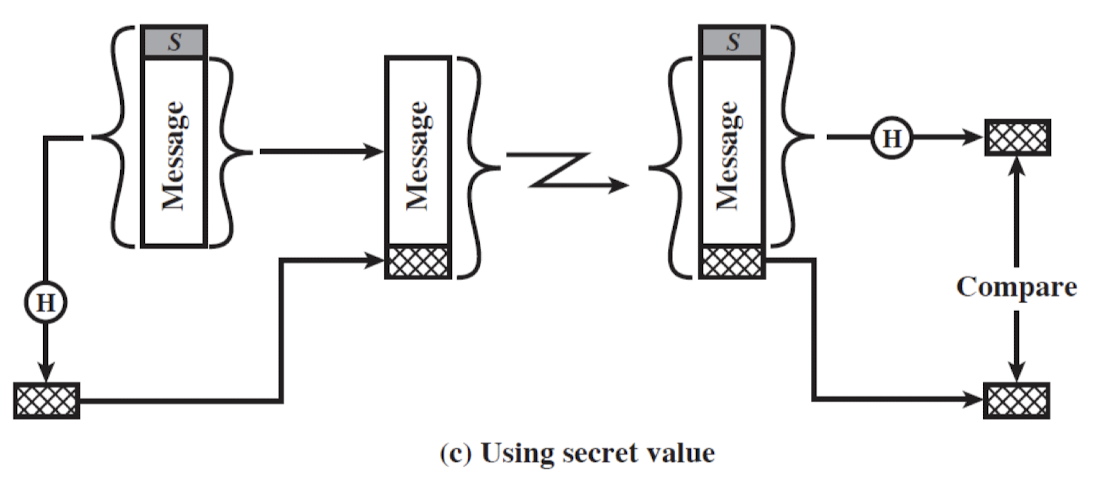
- Encryption SW is quite slow
- Encryption HW cost is not negligible.
- Encryption HW is optimized toward large data size.
- An encryption algorithm may be protected by patent
- Using conventional encryption
Keyed Hash Functions as MACs
- Want a MAC based on a hash function
- Because hash functions are generally faster
- Crypto hash function code is widely available
- Hash includes a key along with message
- Original proposal: KeyedHash = Hash ( Key | Message )
- some weaknesses were found with this
- Eventually led to development of HMAC
Nested MAC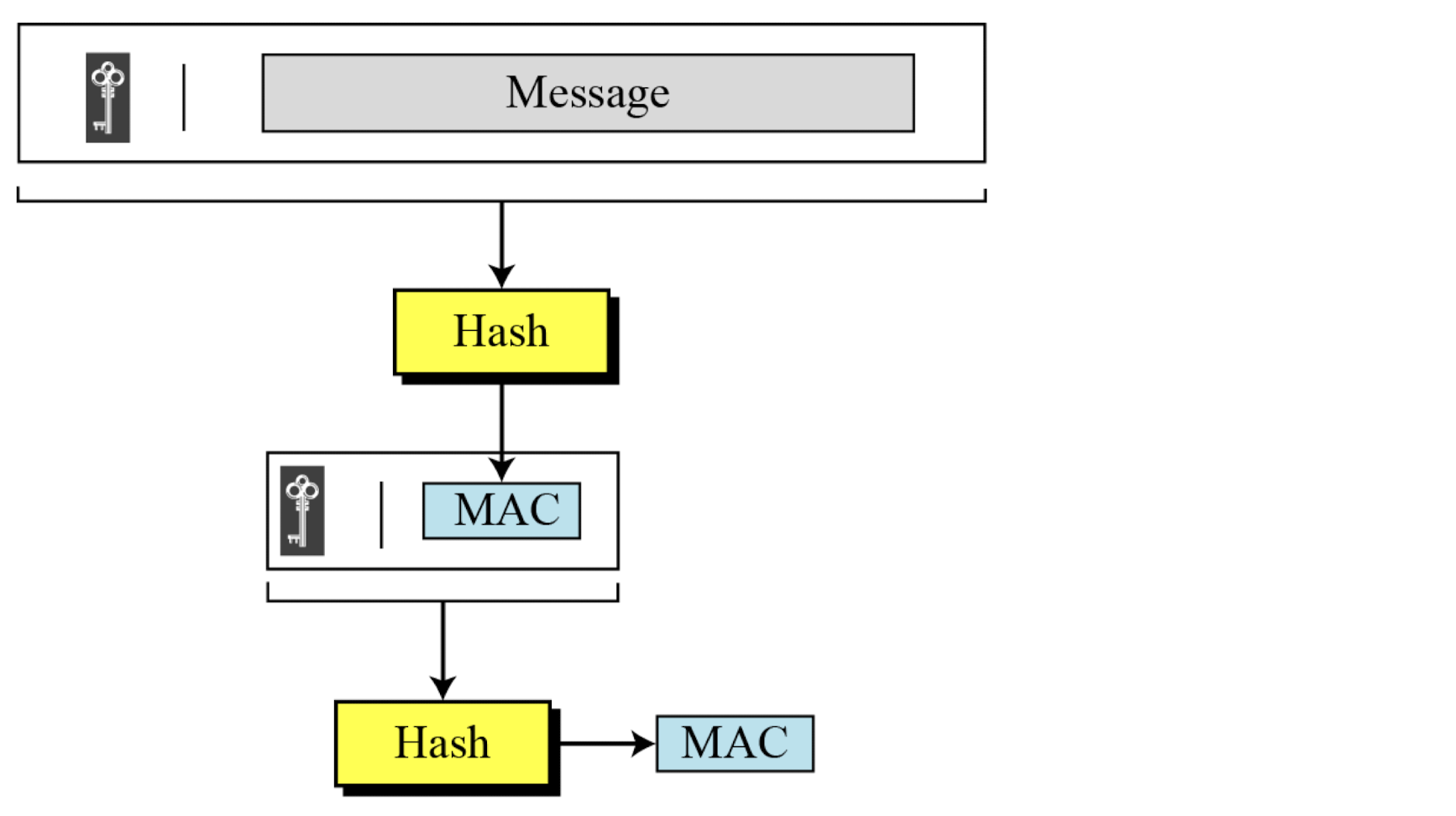
HMAC
- Design Objectives
- Use hash functions without modifications
- Allow for easy replaceability of embedded hash function
- Preserve original performance of hash function without significant degradation
- Use and handle keys in a simple way.
- Have well understood cryptographic analysis of authentication mechanism strength
- Specified as Internet standard RFC2104
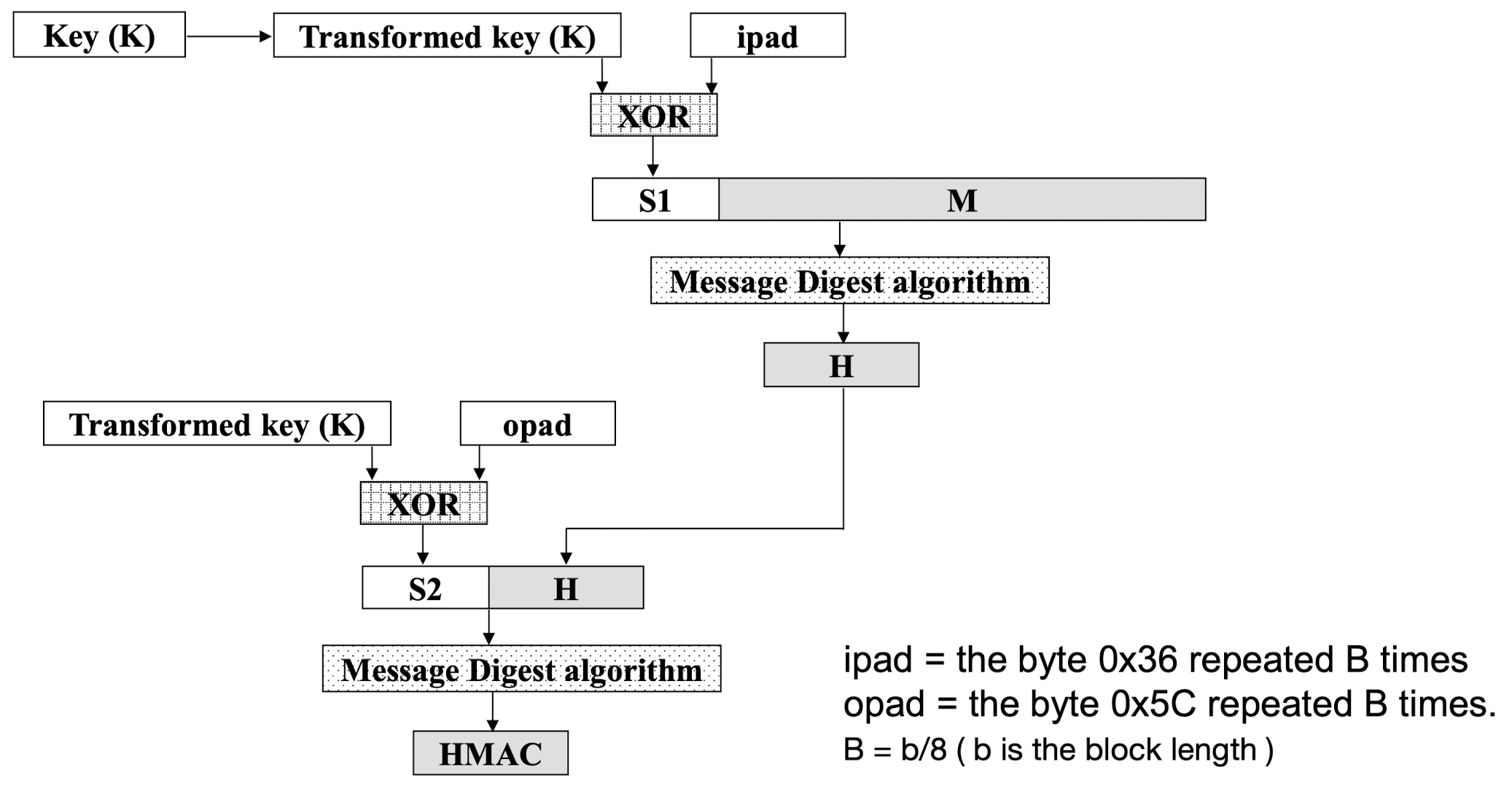
- Uses hash function on the message:
HMAC(M)= Hash[(K+ XOR opad) || Hash[(K+ XOR ipad) || M)] ]- where K+ is the key padded out to size
- opad, ipad(internal padding) are specified padding constants
- Overhead is just a few more hash calculations than the message needs alone
- Any hash function can be used
- eg. MD5, SHA-1, RIPEMD-160, Whirlpool
- HMAC Concept
- Step 1: Make the length of K equal to b
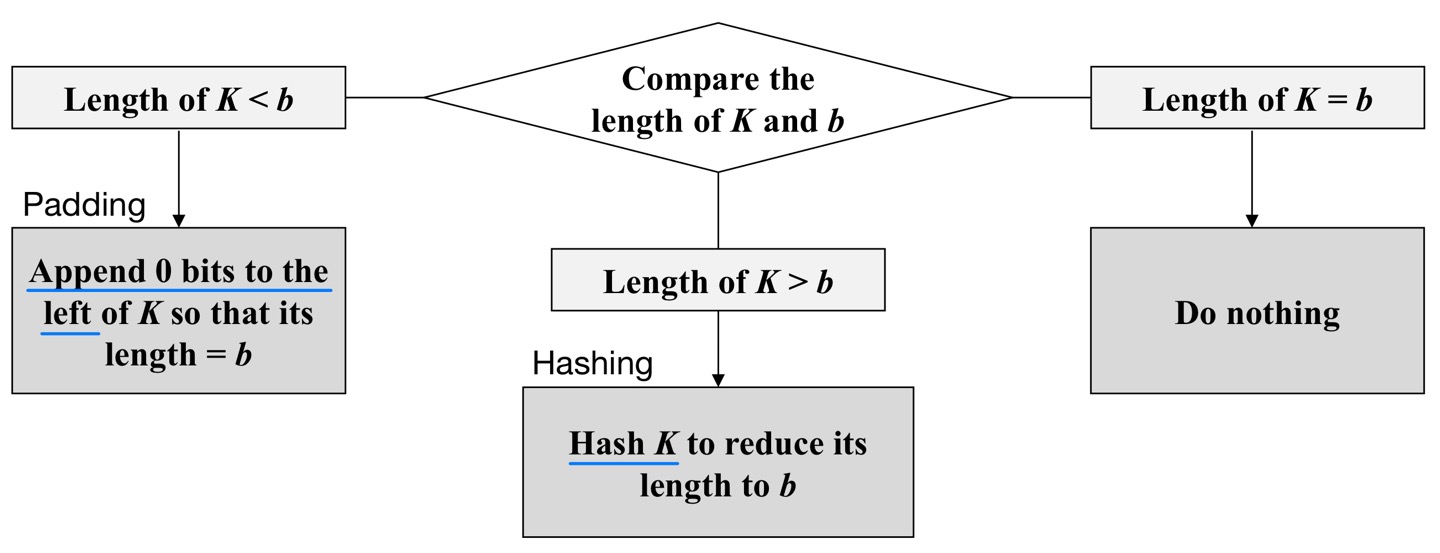
- Step 2: XOR K with ipad to produce S1
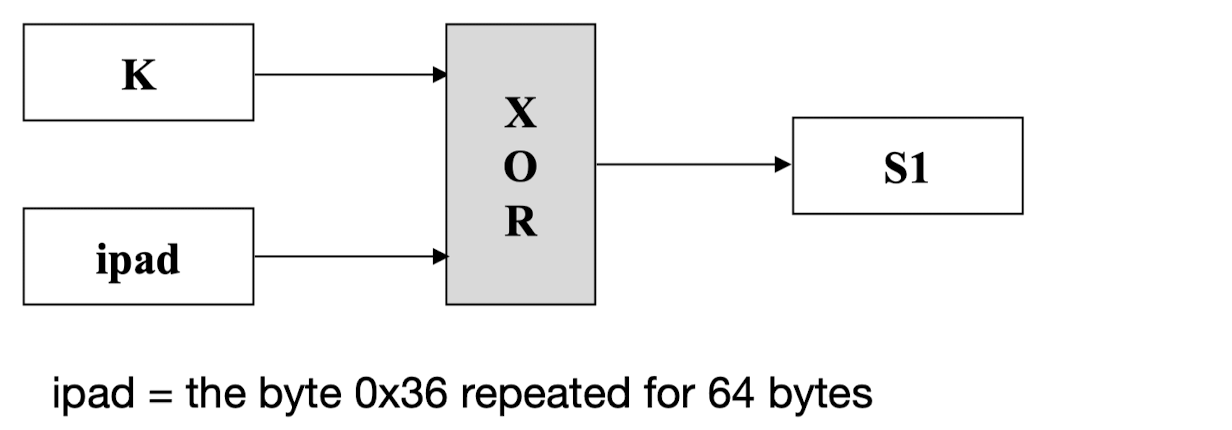
- Step 3: Append M to S1

- Step 4: Message digest algorithm
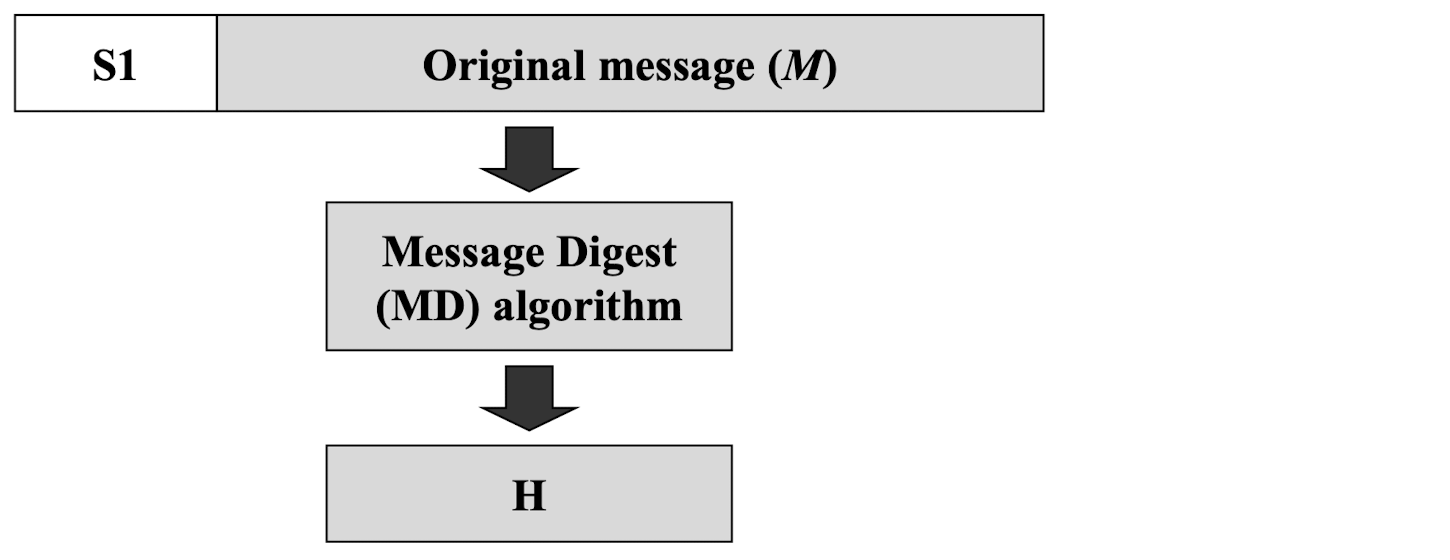
- Step 5: XOR K with opad to produce S2
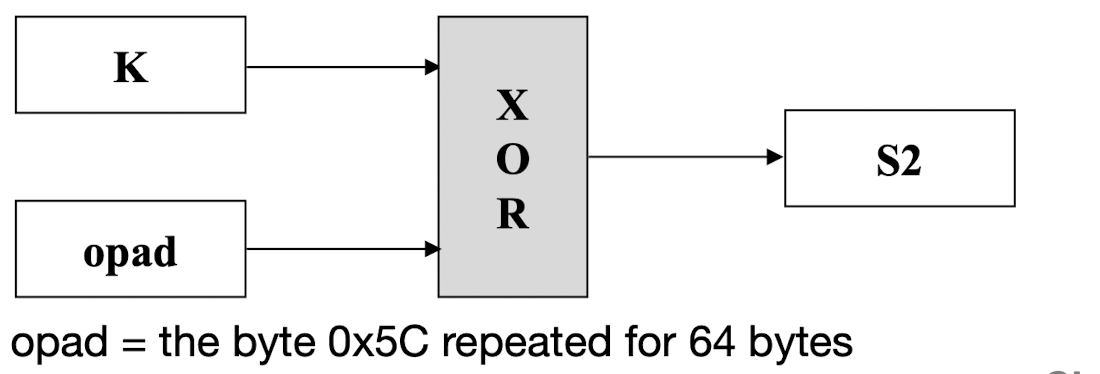
- Step 6: Append H to S2
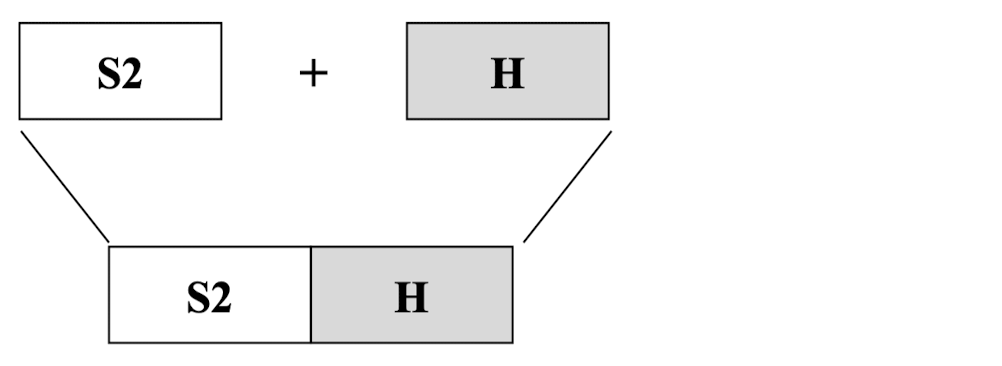
- Step 7: Message-digest algorithm
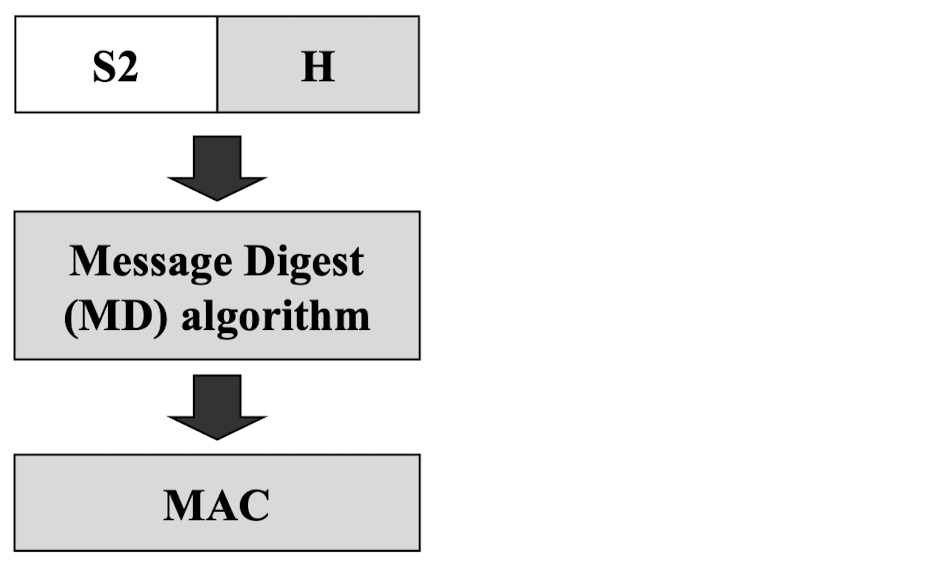
- HMAC Operation
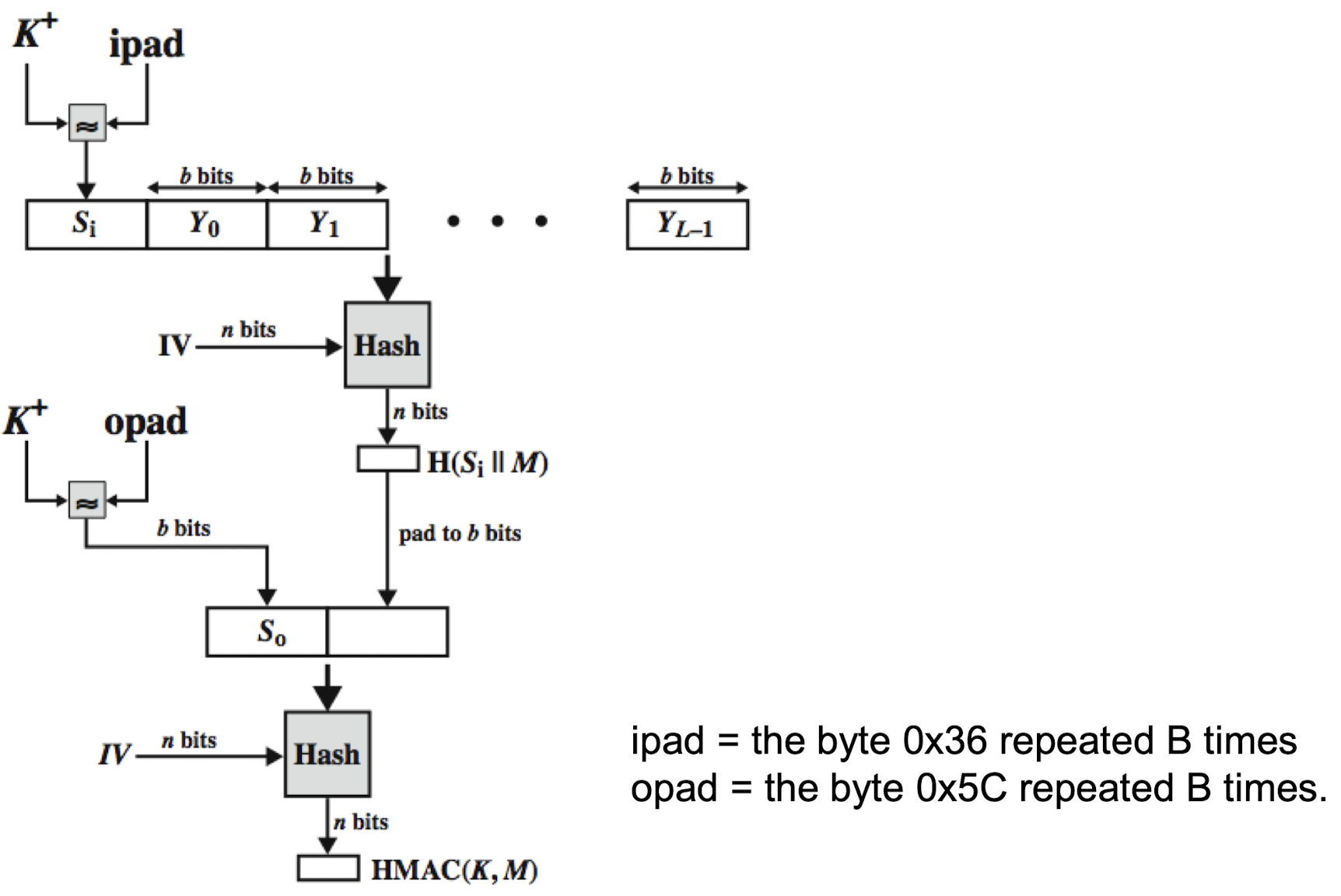
Digital Signatures
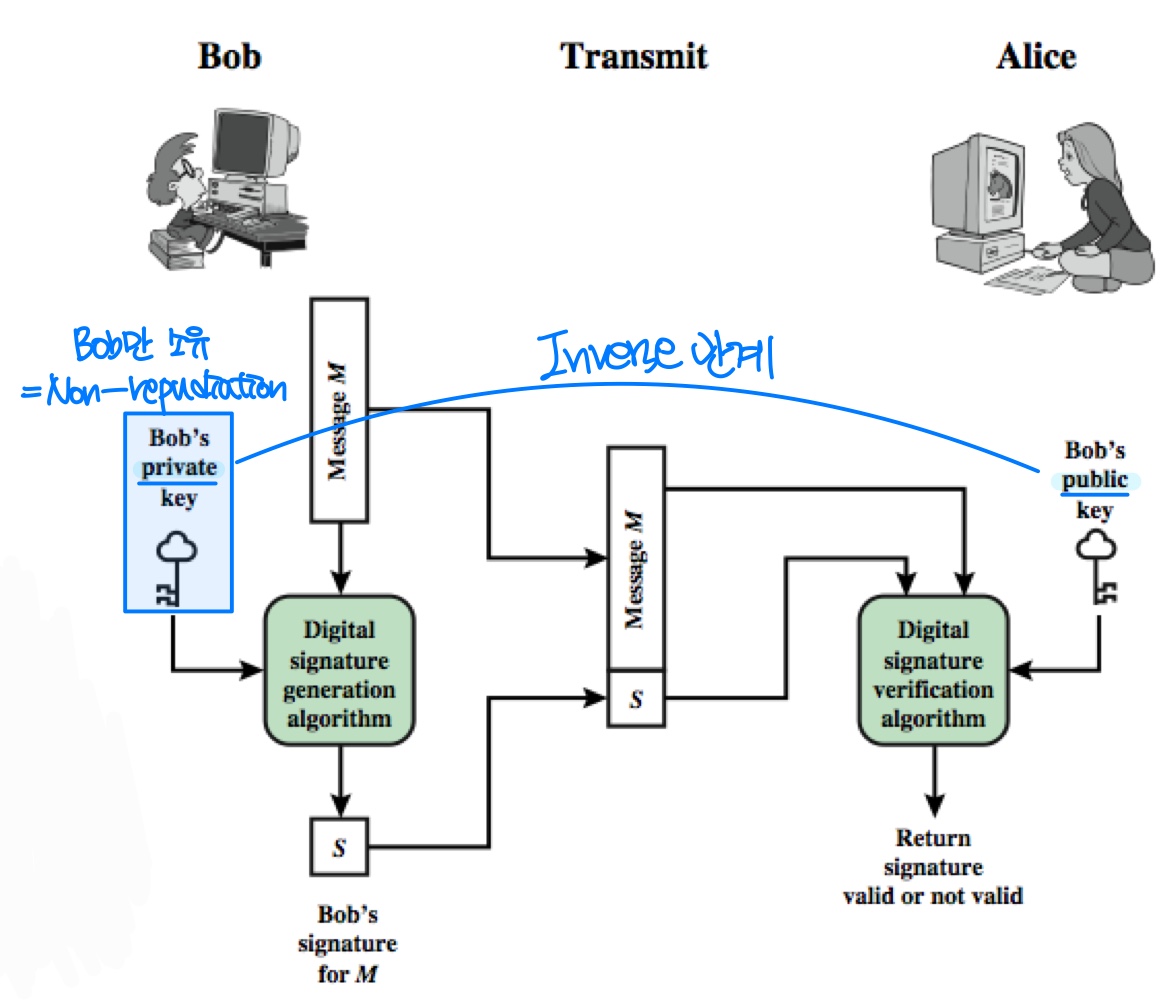
- Digital Signature Concept
- Sender encrypts message or its fingerprint with its private key
- Guarantees that only the sender could have created this message
- Basis for Non-repudiation
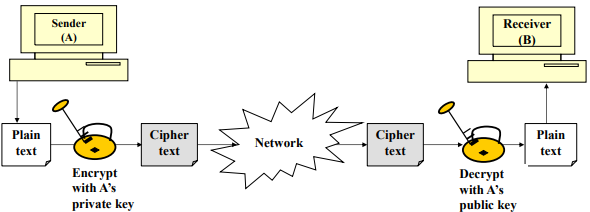
Digital Signatures
- When symmetric key or secret value between Alice and Bob is used in message authentication,
- Alice sends message to Bob with MAC, then Bob knows it is from Alice and the message is not modified. But Alice may deny sending the message. No non-repudiation.
- Alice sends message to Bob with MAC, then Bob knows it is from Alice and the message is not modified. But Alice may deny sending the message. No non-repudiation.
- Digital signatures provide the ability to:
- verify author, date & time of signature
- authenticate message contents
- be verified by third parties to resolve disputes
- Hence include authentication function with additional capabilities
- A digital signature can directly provide validation of identity of originator, message integrity, and non-repudiation; for message confidentiality we still need encryption/ decryption.
- Using a trusted center for non-repudiation
- Non-repudiation can be provided using a trusted party.
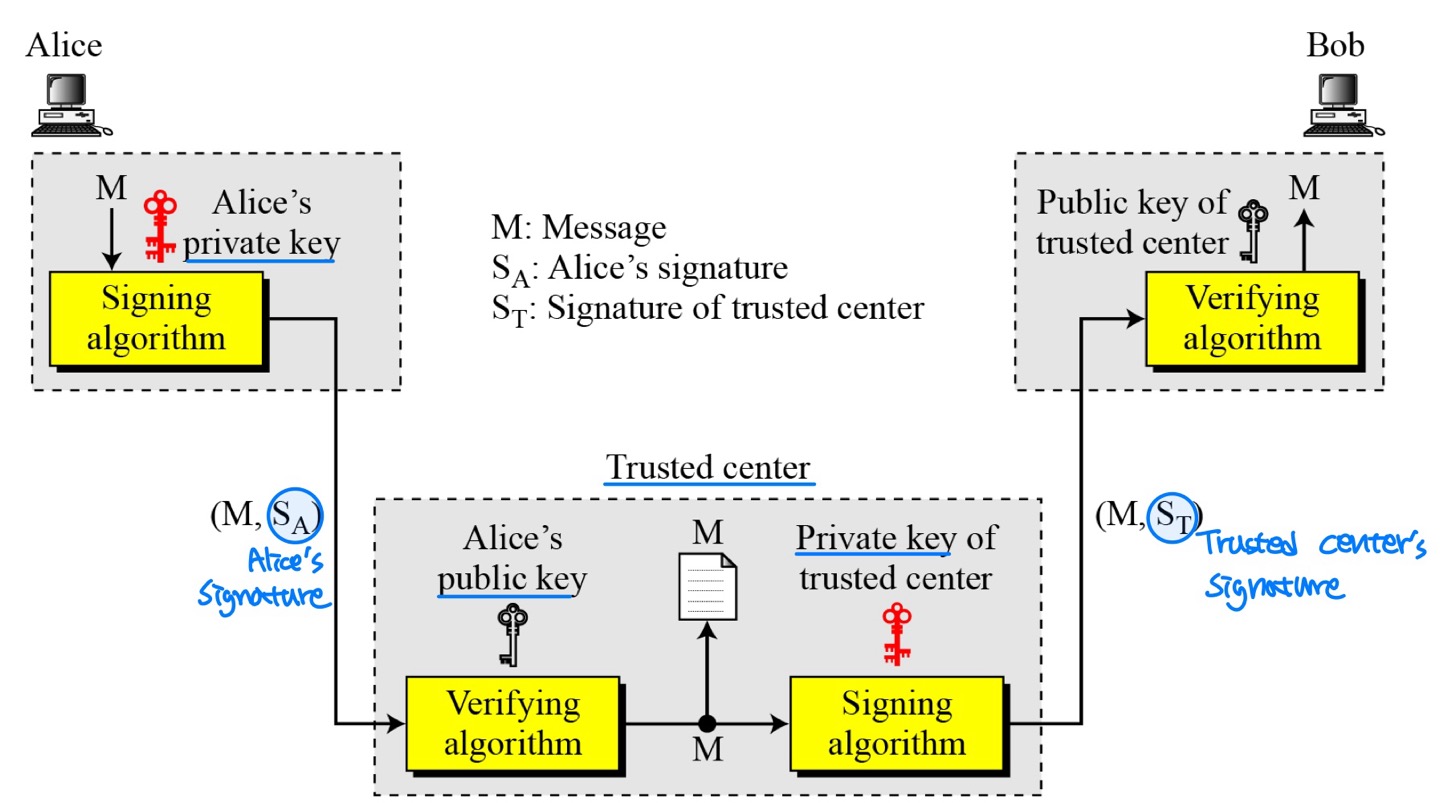
- Non-repudiation can be provided using a trusted party.
- Adding confidentiality to a digital signature scheme
- A digital signature does not provide privacy.
- If there is a need for privacy, another layer of encryption/decryption must be applied.
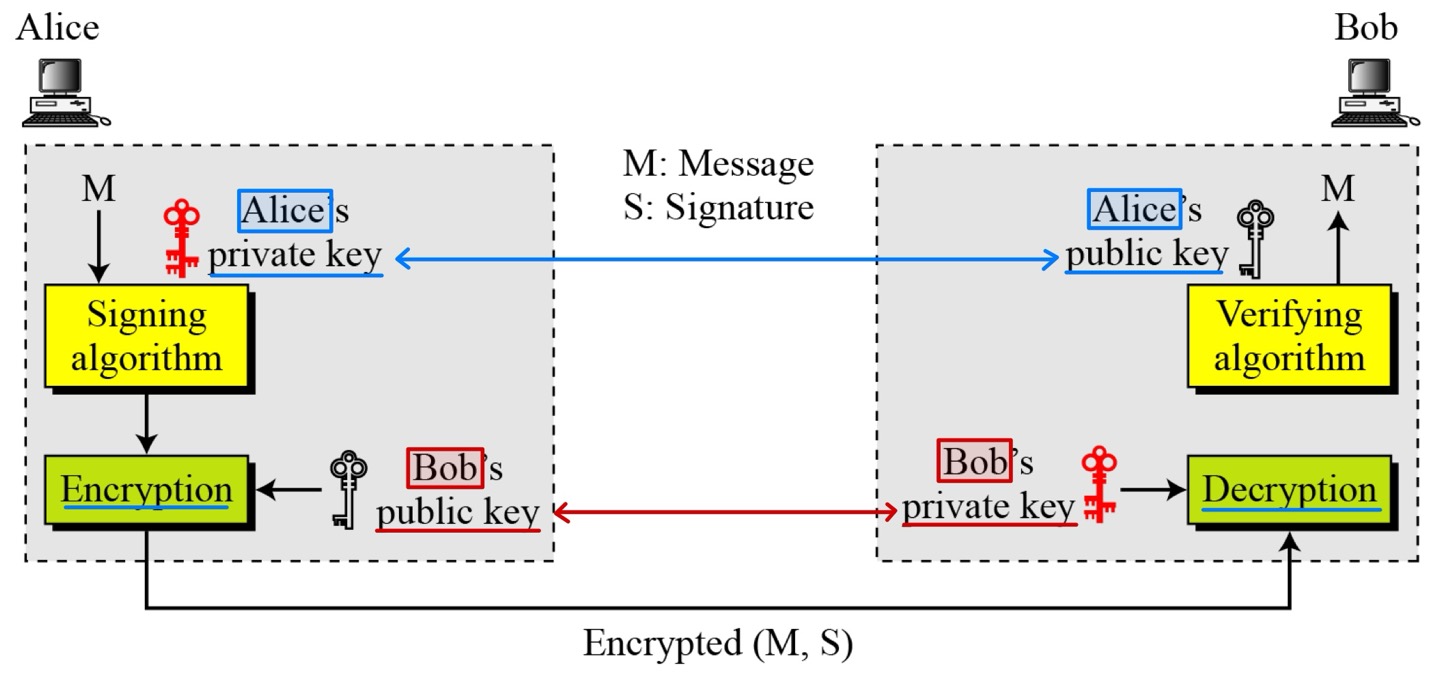
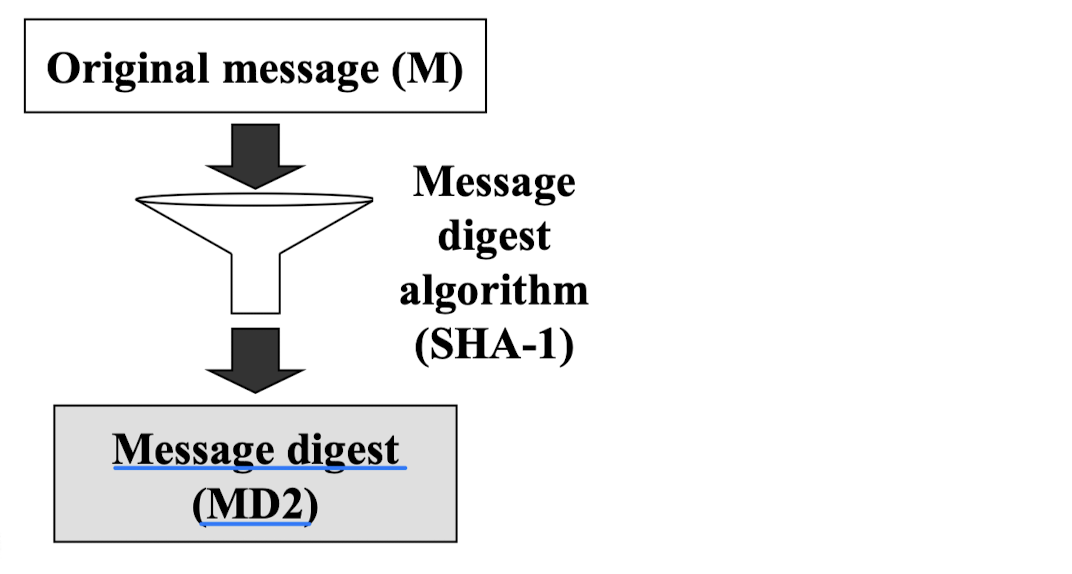
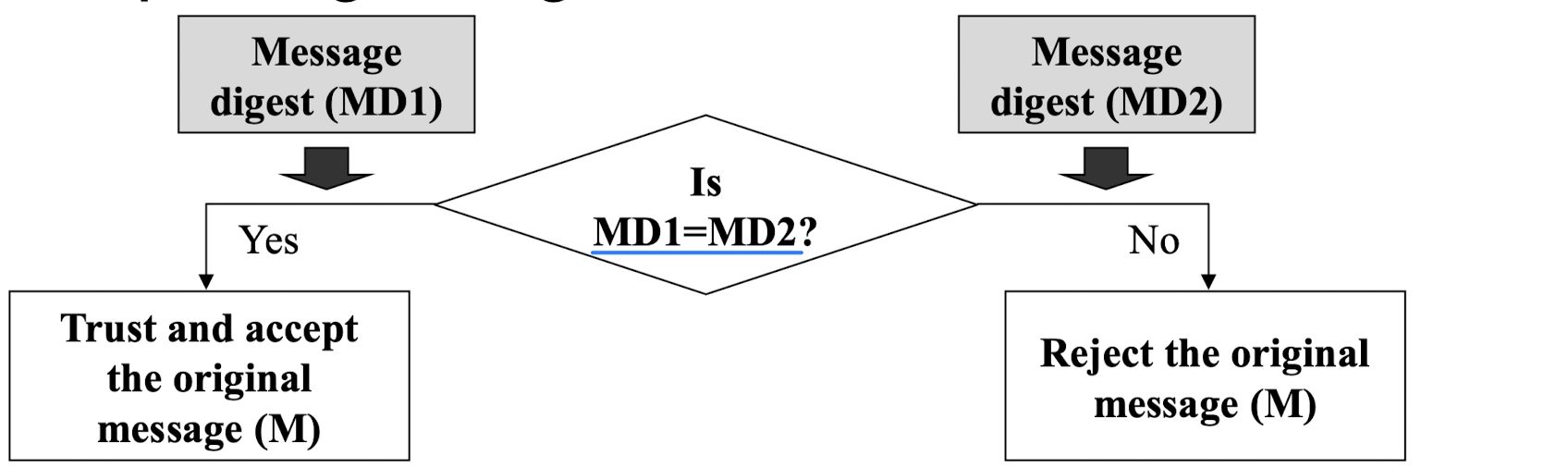
- Step1: Message digest calculation

- Step2: Digital signature creation
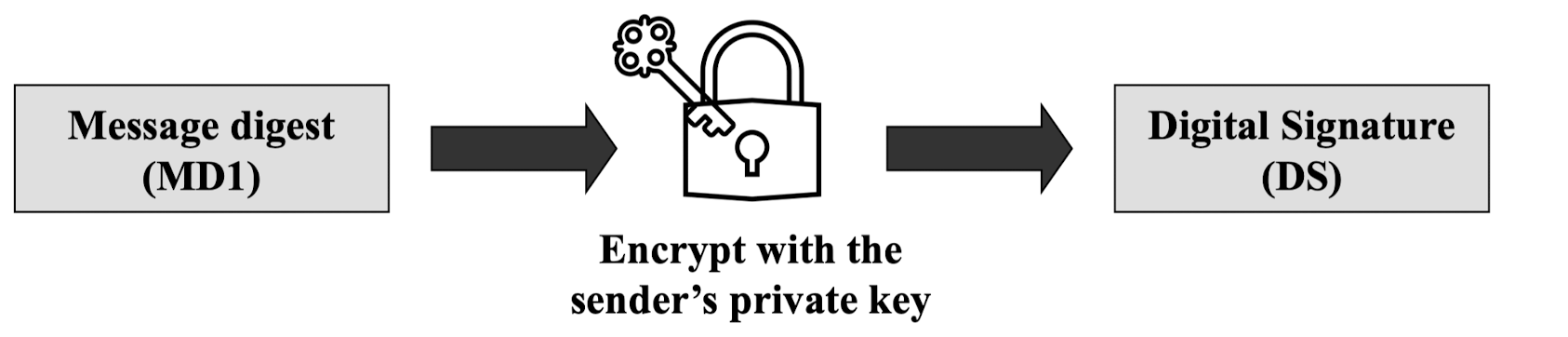
- Step3: Transmission of message and signature
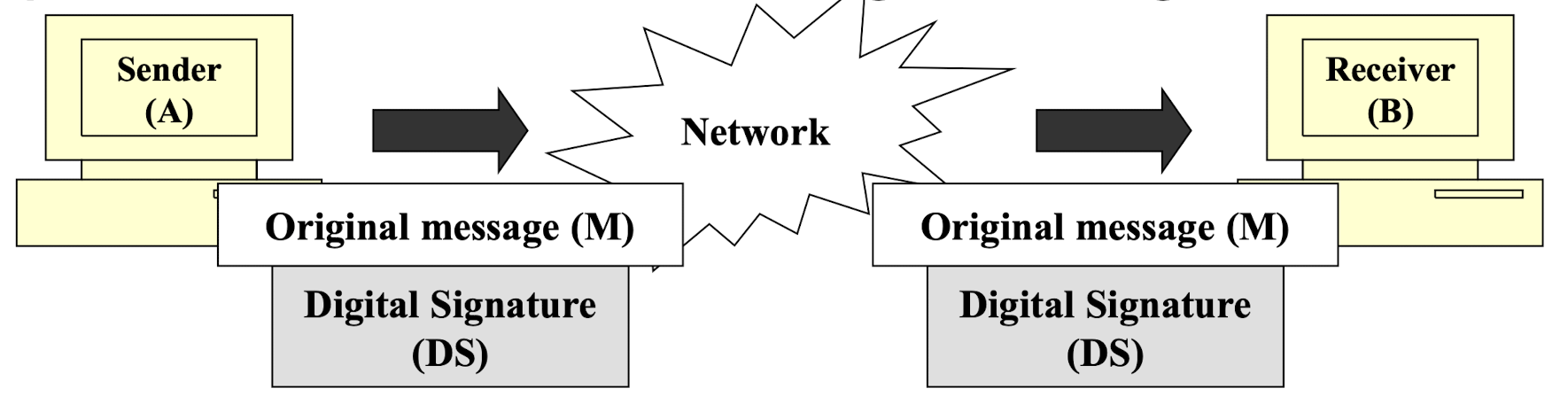
- Step4: Receiver calculates its own MD
- Step5: Receiver retrieves sender’s MD
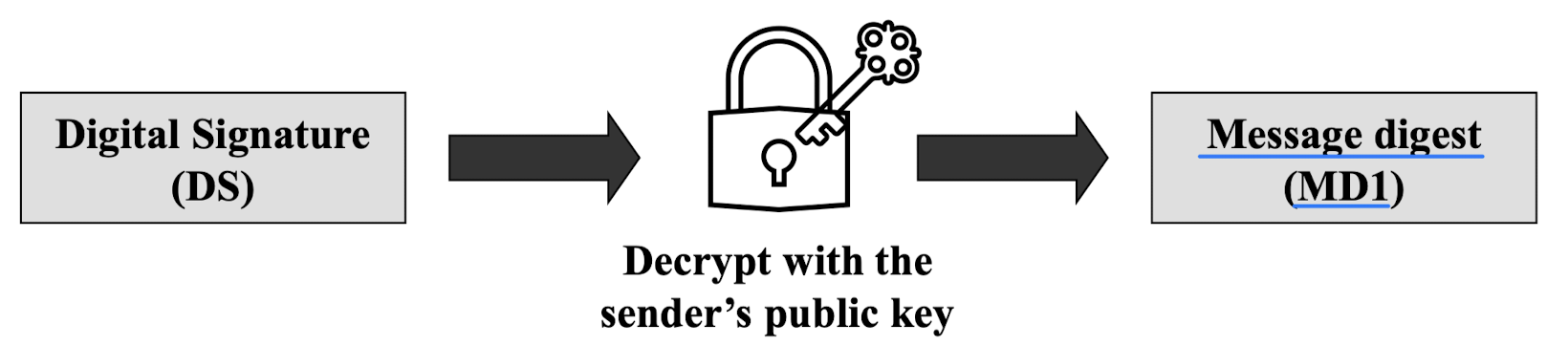
- Step6: Digital signature verification
Key Generation
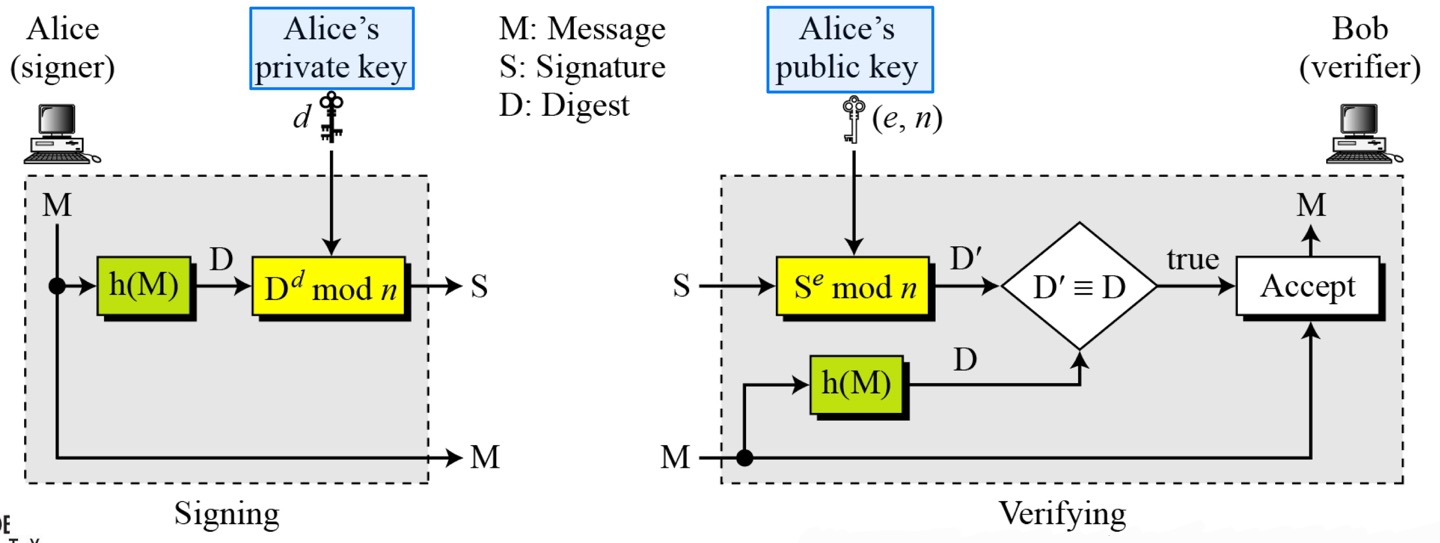
- Key generation in the RSA digital signature scheme is exactly the same as key generation in the RSA
- In the RSA digital signature scheme, 𝑑 is private; 𝑒 and 𝑛 are public.
- RSA Signature on the message digest
HGU 전산전자공학부 고윤민 교수님의 24-2 컴퓨터 보안 수업을 듣고 작성한 포스트이며, 첨부한 모든 사진은 교수님 수업 PPT의 사진 원본에 필기를 한 수정본입니다.

