Asymmetric Key Encipherment - RSA

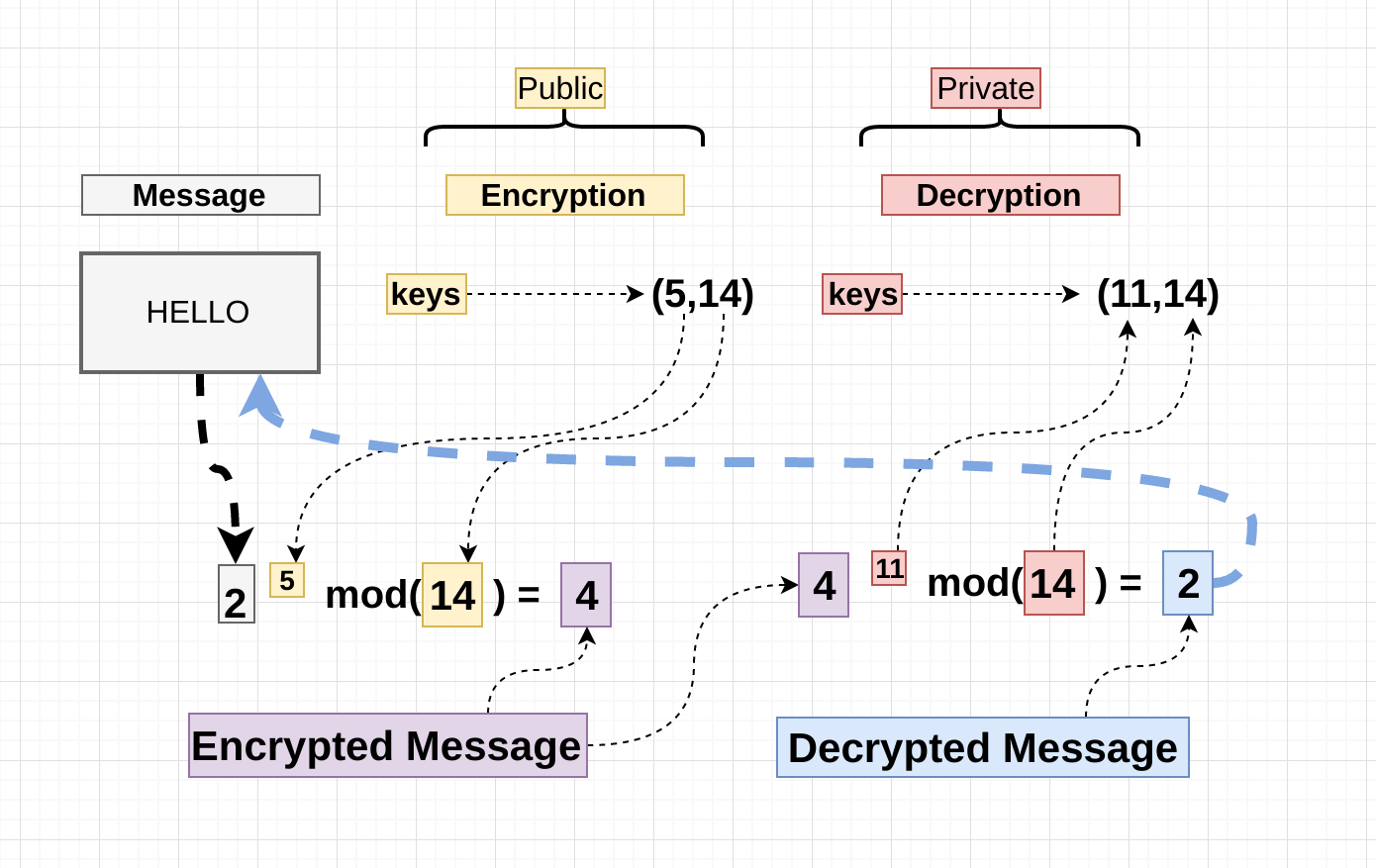
RSA는 대표적인 asymmetric key encipherment 중 하나이다.

Encryption, Decryption 공식은 아래와 같다.

C = Cipher Text, P = Plain Text
Public Key = (e, n), Private Key = d

Encryption: $C = P^{e} \mod n$

Decryption: $P = C^{d} \mod n$

이때 n은 1024bits 이상의 수를 권장한다.

또한 이후에 나올 공식의 증명을 보면 알 수 있듯이 오일러의 정리에 의해서 $P >= n$ 이다.

위 공식을 보면 $P^{e}$, $C^{d}$를 한다.

이때 단순히 P를 e번 곱하거나, C를 d번 곱하는 것은 매우 큰 비용의 연산이 된다.

따라서 이때 이전에 포스팅한 fast exponentiation algorithm을 사용하게 된다.

RSA algorithm 공격에 성공하기 위해선 $\sqrt[e]{C} \mod n$를 계산해야 하는데, 현재까지 알려진 polynomial time algorithm은 없다고 한다.

RSA Key Generation

RSA에서 key를 생성하기 위한 process는 아래와 같다.

1. $p \neq q$인 두개의 큰 소수 p와 q를 선택한다.
   이때 p와 q는 512bits 이상을 권장한다.

2. $n = p * q$인 n을 구한다.
   이때 n은 1024bits 이상이 된다.

3. 오일러 파이 함수의 성질에 따라 $\phi(n) = (p-1) * (q-1)$ 이다.

4. $1 < e < \phi(n)$ 를 만족하는 $\phi(n)$과 서로소인 e를 선택한다.
   $\phi(n)$과 e가 서로소라는 것을 통해 $\mod \phi(n)$에 대하여 e의 역원이 존재한다는 것을 알 수 있다.

5. $\mod \phi(n)$에 대해서 e의 역원인 d를 구한다.
   $d = e^{-1} \mod \phi(n)$

6. Public Key는 e, n이다.

7. Private Key는 d이다.

위 과정에서 e의 역원인 d를 찾기 위해선 1 ~ $\phi(n)$를 모두 대입해야하는데 $\phi(n)$은 대략 1024bits 이상의 굉장히 큰 수 이다.

이를 모두 대입하는 것은 매우 비용이 큰 연산이다.

따라서 이전에 포스팅한 extended euclidian algorithm을 사용하면 된다.

RSA Decryption 공식 정확성 증명

RSA algorithm의 decryption 공식은 아래와 같다.

$P = C^{d} \mod n$

위 decryption 공식에 대해 증명을 해보자.

$P = C^{d} \mod n = (P^{e} \mod n)^{d} \mod n = P^{ed} \mod n$

이때 e와 d는 $\mod \phi(n)$에 대해서 역원이다.

따라서 $e * d = k * \phi(n) + 1$ (이때 k는 어떤 정수이다.)이 된다.

그 이유는 $e * d \div \phi(n)$의 몫이 임의의 정수 k가 될 수 있고, 나머지가 1이기 때문이다.

결과적으로 오일러 파이 함수에 대한 오일러 정리인 $a^{k*\phi(n)+1} \equiv a (\mod n)$ (k는 임의의 정수이고, a < n)에 따라서 아래 수식이 성립한다.

$P = P^{ed} \mod n = P^{k*\phi(n)+1} \mod n = P \mod n$

따라서 $P = C^{d} \mod n$은 증명되고, 오일러 정리에 의해서 P는 n 이하의 수 이어야 한다.

RSA에 대한 공격 - 소인수 분해 공격

RSA algorithm을 공격하기 위해서 소인수 분해 공격을 할 수 있다.

공격자 eve는 공개키 e, n을 알 수 있으므로 $\phi(n)$만 알 수 있다면 e의 역원인 d를 찾는 것은 매우 쉽다.

n으로부터 $\phi(n)$을 찾기 위한 방법은 2가지가 있다.

1. n보다 작으면서 n과 서로소인 수의 개수를 찾는 방법

2. $n = p * q$를 만족하는 소수 p, q를 찾는 방법(소인수 분해 공격)

위 방법 모두 n이 큰 수 이면 매우 시간이 오래 걸리는 작업이다.

따라서 n을 1024bits 이상으로 권고하는 것이다.