Trapdoor One-Way Function

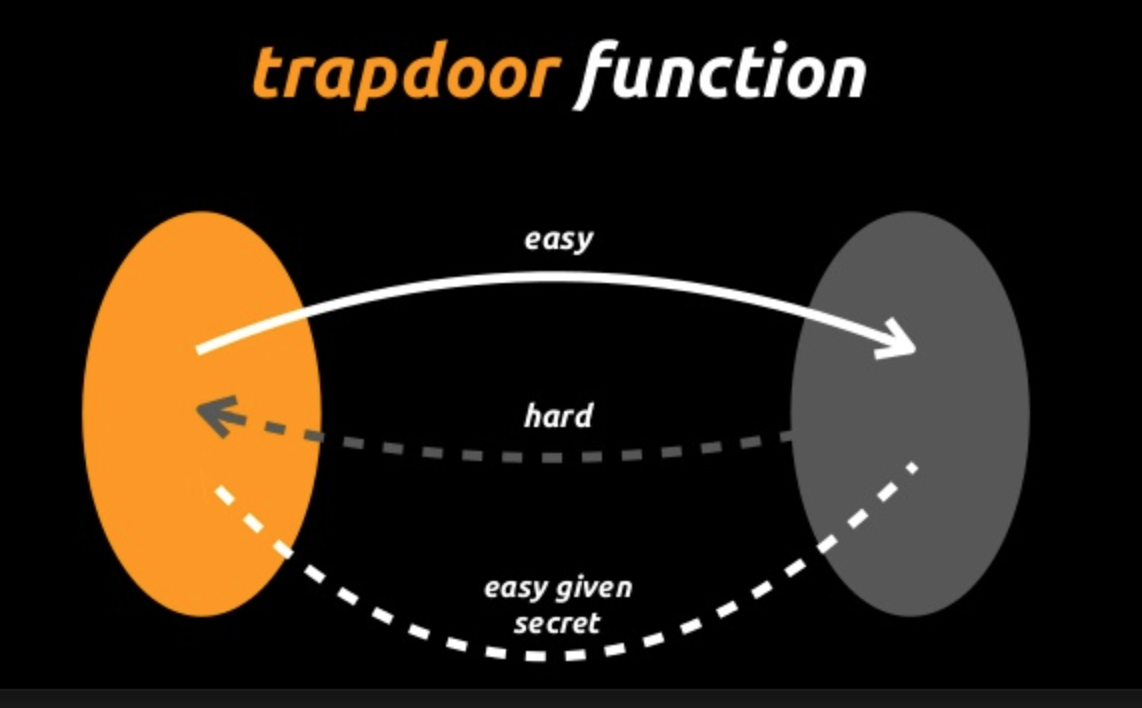
단방향 함수(One-Way Funcion)

단방향 함수(One-Way Function)이란 계산은 쉽지만, 역을 구하는 것은 어려운 함수이다.

이는 역함수가 존재하지 않는다는 말과 비슷하다.

단방향 함수의 대표적인 예로는 hash function이 있다.

실제로 hash function의 역함수가 존재하는지 확인해보자.

Hash Function의 역함수

역함수의 존재 조건은 전단사함수 즉, 일대일대응이어야 한다.

아래 수식을 hash function의 간단한 예로 하자.

$y = x \mod 5$

아래는 위 수식의 그래프이다.

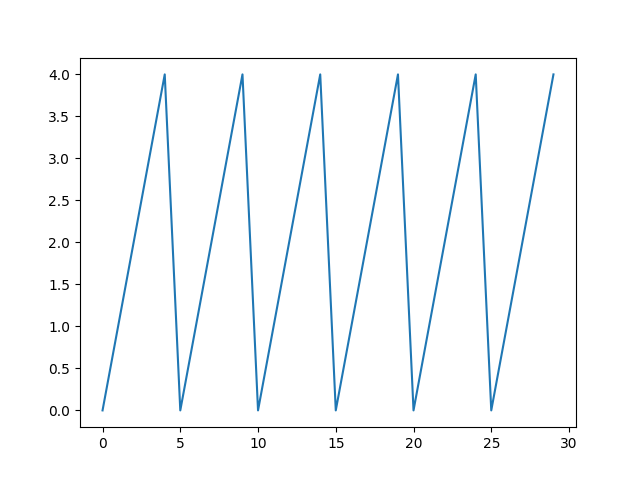
위 그래프를 보면 하나의 y 값에 여러 개의 x값이 존재할 수 있는 것을 볼 수 있다.

그러므로 hash function은 단방향 함수임을 알 수 있다.

Trapdoor One-Way Function

Trapdoor One-Way Function은 단방향 함수의 한 종류로 함수의 역을 구하는 것은 어렵지만, trapdoor라고 불리는 특수한 정보가 있으면 쉽게 역을 구할 수 있는 함수이다.

Asymmetric Key Encipherment의 대표적인 암호 알고리즘인 RSA 암호가 이 trapdoor one-way function의 수학적 아이디어를 기반으로 한다.

Trapdoor One-Way Function의 예

Trapdoor One-Way Function의 예를 들어보자.

$y = x^{k} \mod n$

위 수식에서 x, k, n을 알고 있다면 y를 구하는 것은 쉽다.

하지만 y, k, n을 이용하여 x를 구하는 것은 어렵다.

다만 $k*k^{-1} = 1 \mod n$이 되는 $k^{-1}$를 알면 x를 알 수 있다.

이때 $k^{-1}$를 trapdoor라고 하는 것이다.

즉, x를 알기 위한 수식은 아래와 같다.

$x = y^{k^{-1}} \mod n$