모듈로 연산(Modular Arithmetic)

항상 컴퓨터 과학에 대한 공부를 할때 수학이 나오면 바보가된 기분을 느낀다.

왜냐하면 분명 배운 부분인데 "아... 이거 어떻게 풀더라?" 이러고 있다.

최근 암호학을 공부하면서 modulo에 대해 다시 공부하게 되었다.

익숙하다 싶었는데 이산수학 배울때 생각이 나게 되더라 ^_^

Modulo 연산에 관한 부분은 아래 영상에서 기가 막히게 잘 설명되어 있다.

모듈로 영상 강의 영상 링크

정의

Modulo 연산의 정의는 아래와 같다.

Let $a, r, m \in \Z$ and $m \gt 0$
Then
$a \equiv r \mod m$
if m divides (a-r) ie. $m|(a-r)$

특징

Modulo 연산은 다음과 같은 특징을 가진다.

1. $a \equiv b \mod n \Leftrightarrow b \equiv a \mod n$

$n|(a-b)$가 성립하면 $n|(b-a)$도 성립한다.(그 반대도 성립한다.)

따라서 두 식은 동치이다.

2. $(a \equiv b \mod n) \wedge (b \equiv c \mod n) \Rightarrow a = c$

1번 특징에 의해 $b \equiv c \mod n \rightarrow c \equiv b \mod n$이다.

따라서 $a = c$를 유도할 수 있다.

3. 덧셈, 뺄셈, 곱셈에 한해서 아래 등식 성립

• $(a + b) \mod n = ((a \mod n) + (b \mod n)) \mod n$
• $(a - b) \mod n = ((a \mod n) - (b \mod n)) \mod n$
• $(a * b) \mod n = ((a \mod n) * (b \mod n)) \mod n$

4. 덧셈, 곱셈에 한해서 교환법칙 성립

• $(a + b) \mod n = (b + a) \mod n$
• $(a * b) \mod n = (b * a) \mod n$

5. 덧셈, 곱셈에 한해서 결합법칙 성립

• $((a + b) + c) \mod n = (a + (b + c)) \mod n$
• $((a * b) * c) \mod n = (a * (b * c)) \mod n$

6. 곱셈에 한해서 분배법칙 성립

• $(a * (b + c)) \mod n = ((a * b) + (a * c)) \mod n$

동치류(Equivalence Classes)

Modulo 5 연산을 -8, -3, 2, 7, 12, 17에 대해 해보면

$-8 \mod 5 \equiv 2$
$-3 \mod 5 \equiv 2$
$2 \mod 5 \equiv 2$
$7 \mod 5 \equiv 2$
$12 \mod 5 \equiv 2$
$17 \mod 5 \equiv 2$

로 모두 2와 동치이다.

이렇게 같은 동치를 가지는 수를 동치류라고 한다.

Modulo 5의 동치류는 {..., -8, -3, 2, 7, 12, 17, ...} 이다.

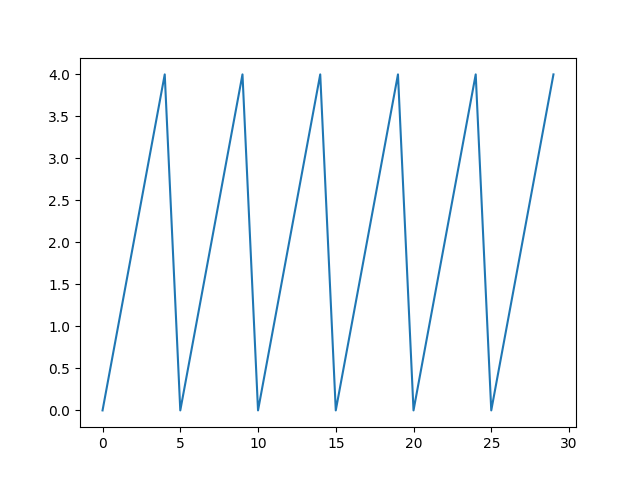
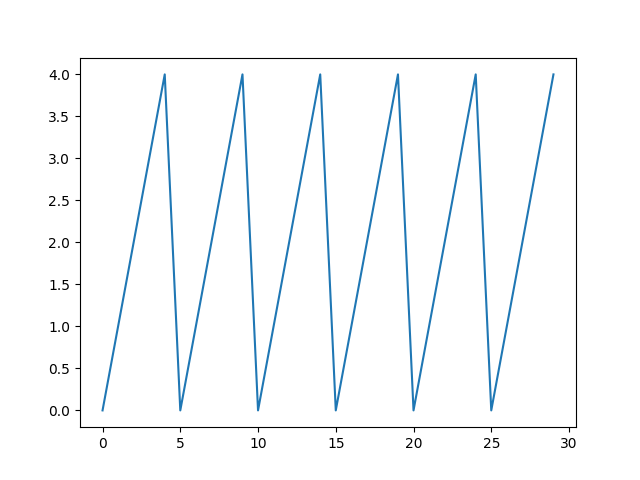
이러한 modulo 연산의 특징으로 인해 0 ~ 30 까지의 수에 modulo 5 연산을 한 함수의 그래프를 matplotlib를 통해 생성해보면 아래와 같다.

항등원(Identity)

항등원(Identity)이란 임의의 수 a에 대하여 어떤 수를 연산했을 때 a를 결괏값으로 만드는 그 어떤 수를 뜻한다.

• $(a + 0) \mod n = a \mod n$
• $(a * 1) \mod n = a \mod n$

역원(Inverse)

역원(Inverse)이란 임의의 수 a를 어떤 수와 연산했을 때 항등원을 결괏값으로 만드는 그 어떤 수를 뜻한다.

• $a + (-a) = 0 \mod n$
• $a * a^{-1} = 1 \mod n$
  단, $a^{-1}$은 a와 n이 coprime일 때만 존재한다.
  즉, gcd(a, n) = 1 일 때만 모듈로 곱 연산에서 inverse가 존재할 수 있다.