확장 유클리드 알고리즘(Extended Euclidean Algorithm)

아래와 같은 수식에서 $k$의 역원인 $k^{-1}$를 찾아내기 위해 가장 간단한 방법은 0 ~ n-1까지 $k^{-1}$ 위치에 brute force 하는 것일 것이다.

$k * k^{-1} = 1 \mod n$(Assumption: gcd(k, n) = 1)

암호 알고리즘 특성상 위와 같은 수식에서 n의 크기가 커지는 경우가 생길 수 있다.

그러면 그때 역원을 구하는 overhead는 너무 크다.

그때 확장 유클리드 알고리즘(Extended Euclidean Algorithm)을 사용한다.

유클리드 알고리즘(Euclidean Algorithm)

먼저 확장 유클리드 알고리즘을 보기 전에 유클리드 알고리즘부터 보자.

유클리드 알고리즘(Euclidean Algorithm)은 최대공약수(GCD : Greatest Common Divisor)를 구할 때 사용하는 알고리즘이다.

$q = r_{1} \div r_{2}$
$r = r_{1} \mod r_{2} = r_{1} - q * r_{2}$

유클리드 알고리즘은 위 그림과 같은 프로세스를 가진다.

프로세스에서 보면 알 수 있듯이 $r_{2}$가 0일 때 $r_{1}$의 값이 n, b의 최대공약수가 된다.

확장 유클리드 알고리즘(Extended Euclidean Algorithm)

확장 유클리드 알고리즘(Extended Euclidean Algorithm)은 모듈러 곱(modular multiplication) 연산의 inverse를 빠르게 찾게 하는 알고리즘이다.

확장 유클리드 알고리즘은 유클리드 알고리즘을 응용한 알고리즘이다.

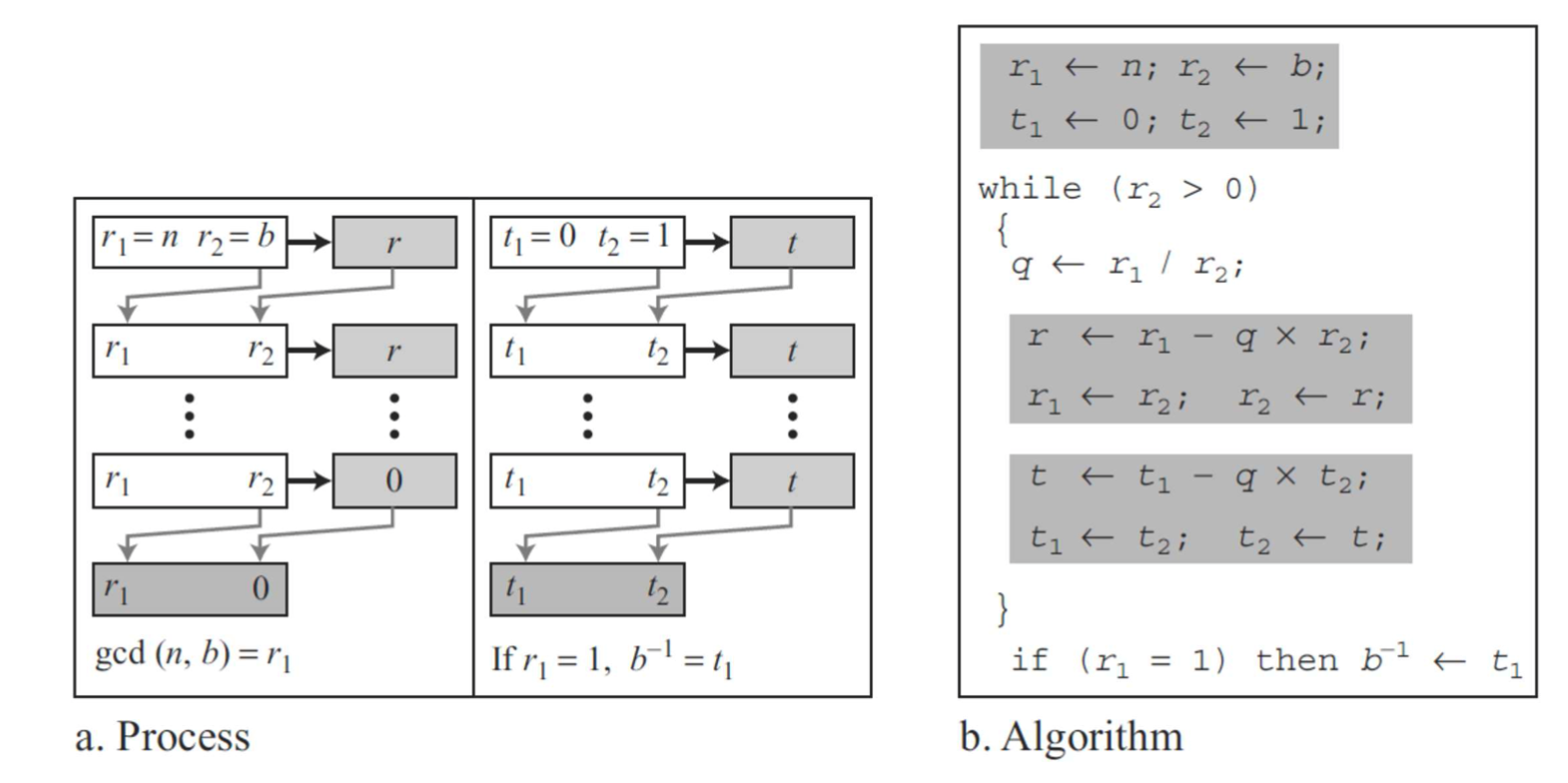
만약 계산 결과 $t_{1}$이 음수 라면 $t1 \mod n$ 혹은 $t1 + n$을 해준 결괏값이 inverse가 된다.

결국 모듈러 곱 연산의 inverse가 존재한다고 가정한다면 $r_{2}$가 0일 때 $r_{1}$이 1이 된다.

그리고 $r_{1}$이 1일 때 $t_{1}$이 modulo n의 곱셈에 대한 b의 inverse가 된다.

아래가 확장 유클리드 알고리즘을 python으로 구현한 코드이다.

def extendedEuclidean(n, b):
    r1, r2 = n, b
    t1, t2 = 0, 1
    while r2:
        q = r1 // r2
        r = r1 - q * r2
        r1, r2 = r2, r
        t = t1 - q * t2
        t1, t2 = t2, t

    # if r1 != 1 => n, b가 coprime이 아니므로, b의 inverse는 존재하지 않는다.
    if r1 != 1:
        return 0
    if t1 < 0:
        t1 = n + t1
    return t1