코딩테스트 준비를 하는 도중
https://leetcode.com/problems/course-schedule/description/문제를 해결하기 위해 조사하던중 DAG에 대해서 공부하게 됐다.
위 문제는
Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false문제해석
numCourses : 과목의 수
prerequisites : 선행과목 정보
prerequisites의 경우 수학, 과학이라는 과목이 있다고 가정하면
[수학, 과학] 는 수학을 듣기위해서는 과학이 선행되어야 한다는 의미이다.
Input값 확인
prerequisites = [[1,0],[0,1]] 의 경우에 [1, 0]에서 1보다 0이 먼저 선행되어야 하지만
[0, 1]에서 0보다 1이 먼저 선행해야한다는 모순이 발생했기 때문에
output으로 false가 나온 모습을 확인할 수 있다.
해결방법
즉 prerequisites에 들어있는 과목들의 순서를 배정할 수 있냐 없냐라고 해석할 수 있는데 이와 같은 문제는 위상정렬을 사용하면 쉽게 해결 할 수 있다.
바로 위상정렬을 풀기위한 그래프가 DAG(사이클이 없는 방향그래프)라고 할 수 있다.
DAG에 대해서 알아보자!
사이클이 없는 방향그래프 (DAG)
Directed acyclic graph라는 이름에서 부터 본인의 특징을 어필하고있는 그래프는 방향성이 존재해야 하며, acyclic(비순환) 해야 하는 그래프이다.
즉 그래프상에서 cyclic(순환)이 없어야 한다는 이야기이다. 순환이 없다는 말은 한 지점에서 출발 했을 때 다시 출발 지점으로 돌아올 수 없다는 것을 뜻한다.
위상 정렬(Topology Sort)
순서가 정해져 있는 작업을 차례로 수행해야 할 때 그 순서를 결정해주기 위해 사용하는 알고리즘
이러한 위상 정렬은 DAG에만 적용이 가능하기 때문에
- DAG가 아니라고 판단할 수 있다.
- 순서가 정해져 있는 작업의 순서를 결정할 수 있다.
구현방법
큐(Queue)를 이용한 방식
- 진입차수가 0인 정점을 큐에 삽입한다.
- 큐에서 원소를 꺼내 연결된 모든 간선을 제거한다.
- 간선 제거 이후에 진입차수가 0이 된 정점을 큐에 삽입한다.
- 큐에 값이 없을 때 까지 2번 ~ 3번 과정을 반복한다. 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재하는 것이고, 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상 정렬의 결과가 된다.
예시
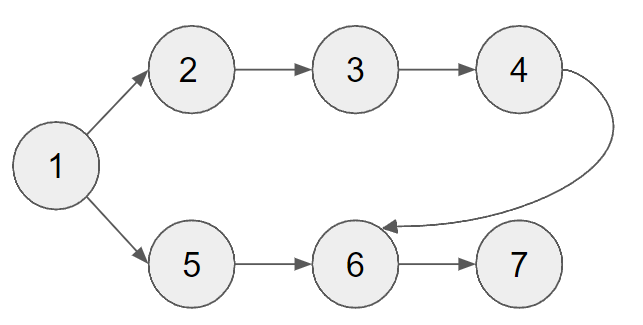
다음과 같은 그래프가 있다고 가정한 뒤 각 정점과 진입차수 정보를 기입해야 한다.

진입차수는 해당 정점으로 들어오는 노드의 수라고 생각하면 된다. 6을 확인해보면 4와 5가 진입하고 있기 때문에 진입차수가 2인것이다.
자 그러면 구현방법의 순서대로 진행해보도록 하겠다.
진입차수가 0인 정점을 큐에 먼저 삽입해야하기 때문에 1을 삽입한다.

이제 큐에서 원소를 꺼내 연결된 모든 간선을 제거 합니다. 그러면 큐에 있는 원소 1이 꺼내지게 되고 1과 연결된 모든 간선을 제거 해줍니다.
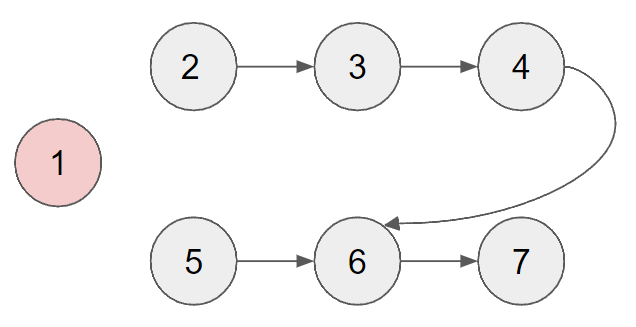
간선을 제거 한 뒤에는 진입차수가 업데이트 되기 때문에 이때 진입차수가 0이 된 정점을 큐에 삽입합니다. (2와 5가 진입차수가 0이기 때문에 큐에 삽입한다.)

그럼 아직 큐가 비어있지 않기 때문에 큐에서 원소를 빼주고 연결된 간선을 제거 합니다.
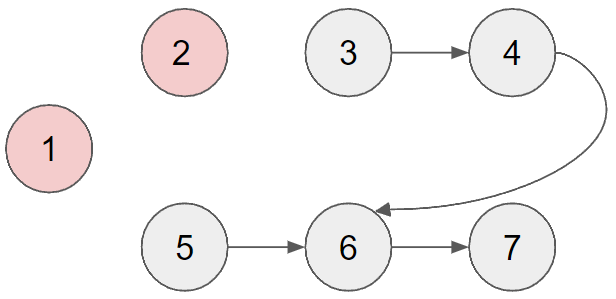
이 행위를 큐가 비어있을때 까지 반복하다 보면은 1 - 2 - 5 - 3 - 4 - 6 - 7 순으로 큐에서 꺼내지게 되는데 이게 바로 위상정렬을 수행한 순서가 결정된 것이다.
해결코드
이 원리를 이용하여 해당 문제에 적용한 코드는 다음과 같다.
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
def topology_sort():
result = [] # 정점순서를 담아줄 리스트
q = deque()
# 진입차수가 0인 정점을 큐에 넣는 코드
for i in range(numCourses):
if indegree[i] == 0:
q.append(i)
while q:
current = q.popleft()
result.append(current)
for i in graph[current]:
indegree[i] -= 1 # 연결된 간선을 제거하는 코드
if indegree[i] == 0:
q.append(i)
return result
graph = [[] for _ in range(numCourses+1)]
indegree = [0]*(numCourses+1)
for i in prerequisites:
u, v = i
graph[u].append(v)
indegree[v] += 1
answer = len(topology_sort())
if answer == numCourses:
return True
else:
return False
