230620 Today I Learned

어제 이진 삽입 정렬에 대해 공부해보니 이진 탐색에 대해 좀 더 알아보고 싶어졌다.

이미지 출처 : Yusang 블로그

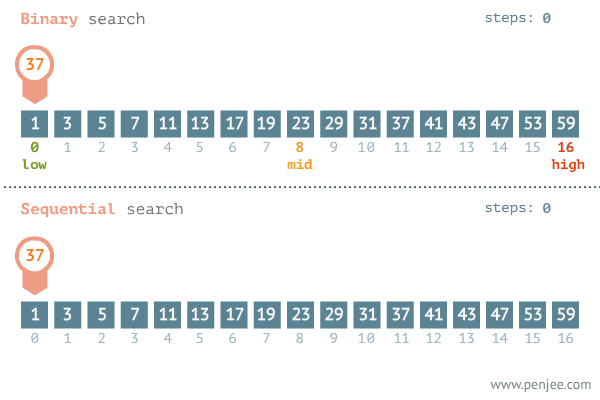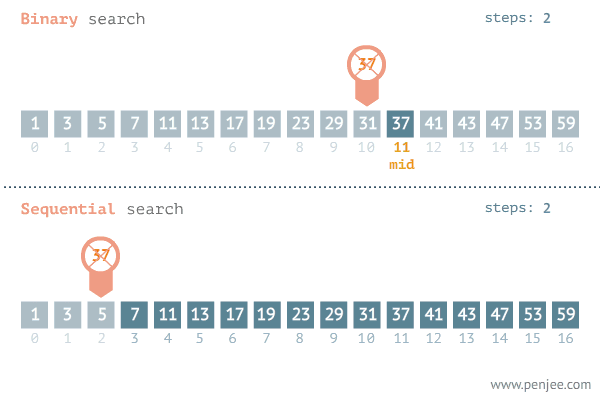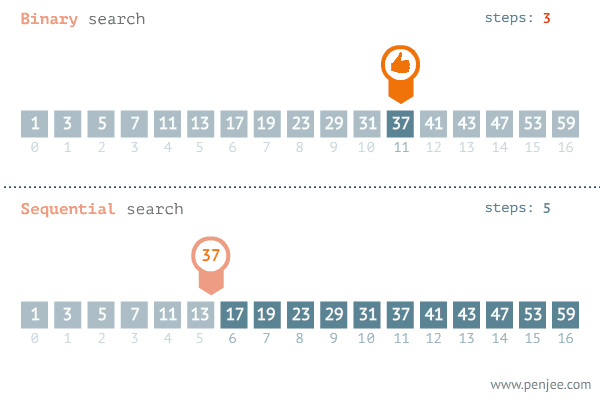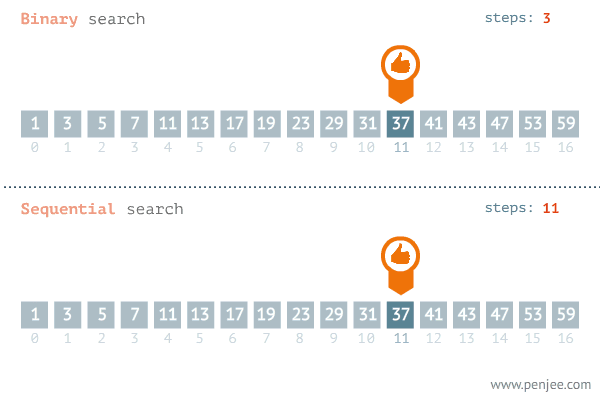
순차탐색(Sequential Search)

리스트나 배열 같은 선형 데이터 구조에서 원하는 값을 찾기위해 처음부터 순서대로 탐색하는 방법

• 정렬되지 않은 배열(리스트)에서도 사용할 수 있다.

• 하지만 최악의 경우 리스트의 모든 요소를 확인해야 하므로 비효율적이다.

• 시간복잡도는 O(n)

java로 구현

  private static int sequentialSearch(int[] array, int target){
  // for문으로 배열의 처음부터 끝까지 비교한다.
    for (int i = 0; i < array.length; i++) {
      if (array[i] == target){
        return i;
      }
    }
    return -1;
  }

이진탐색(Binary Search)

리스트나 배열 같은 선형 데이터 구조에서 원하는 값을 찾기위해 탐색 범위를 절반씩 계속 나눠서 탐색하는 방법

• 배열(리스트)은 반드시 정렬이 되어있어야 한다.

• 배열에서 중간 값을 비교하고 크면 오른쪽, 작으면 왼쪽 범위로 절반씩 줄여서 다시 비교한다.(오름차순 정렬 기준)

• 매번 탐색범위를 절반씩 줄여가므로 탐색 속도가 순차탐색에 비해 빠르다.

• 시간복잡도는 O(log n)

O(n)과 O(log n)의 차이?

• 실제로 계산해보면 체감보다 차이가 더 크다.

• 8,589,934,592(약 85억)개의 원소가 있는 리스트에서 특정 값을 찾는다고 생각해보자.

• O(n)인 순차탐색으로 찾으려면 최악의경우 8,589,934,592번의 비교연산이 필요하다.

• O(log n)인 이진탐색으로 찾으려면 최악의 경우 33번의 비교연산으로 값을 찾을 수 있다.

• 물론 해당 리스트는 정렬이 되어있어야 한다.

java로 구현

  private static int binarySearch(int[] array, int target){
//    배열의 시작 인덱스를 low, 마지막 인덱스를 high로 설정
    int low = 0;
    int high = array.length-1;
//    값을 찾을 때 까지 while문으로 반복. low가 high와 일치하는 선까지 반복한다.
    while (low <= high){
//      low와 high의 중간값인 mid를 target과 비교
      int mid = (low + high) / 2;
//      일치하면 mid값 반환
      if (array[mid] == target){
        return mid;
//        mid보다 target이 크면 mid 다음값으로 low를 올려서 while문 반복
      } else if (array[mid] < target){
        low = mid + 1;
//        mid보다 target이 작으면 mid 이전값으로 high를 내려서 while문 반복
      } else {
        high = mid - 1;
      }
    }
    return -1;
  }

• while 반복문 말고 재귀적으로 mid와 target이 일치하지 않을 경우 return값으로 다시 이진탐색을 실행하는 방법도 있다.

결과

  public static void main(String[] args) {
    int[] array = {1,2,7,5,4,3,9,6,8,10};
    int target = 8;
    int result = sequentialSearch(array, target);
    if (result == -1){
      System.out.println("순차탐색 결과, 타겟 값이 배열에 없습니다.");
    } else {
      System.out.println("순차탐색 결과, 타겟 값과 일치한 배열의 인덱스는 " + result+ "입니다.");
    }

//    이진탐색을 위한 정렬
    Arrays.sort(array);
    System.out.println("이진탐색을 위해 배열을 정렬합니다.");
    int result2 = binarySearch(array, target);
    if (result2 == -1){
      System.out.println("이진탐색 결과, 타겟 값이 배열에 없습니다.");
    } else {
      System.out.println("이진탐색 결과, 타겟 값과 일치한 배열의 인덱스는 " + result2 + "입니다.");
    }
  }