230629Today I Learned

오늘은 퀵정렬 알고리즘에 대해 알아보고 구현해보았다.

퀵정렬

분할 정복 방법을 기반으로 평균적으로 매우 빠른 수행 속도를 가져 널리 사용되는 정렬 알고리즘

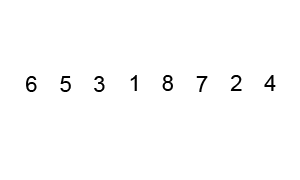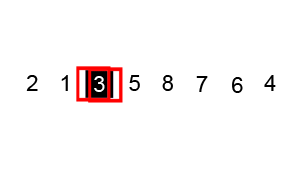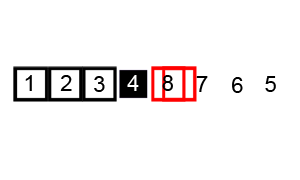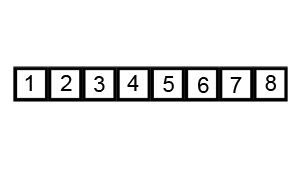
• 정렬 과정
  배열 안의 한 요소를 pivot(피벗)으로 선택한다.
  pivot을 기준으로 작은 요소는 모두 왼쪽으로, 큰 요소는 오른쪽으로 옮긴다.
  pivot을 제외한 왼쪽 배열과 오른쪽 배열을 부분배열로 나눠서 그 안에서 pivot을 새로 정해 정렬한다.
  재귀를 사용해 부분배열이 더이상 분할되지 않을 때까지 반복한다.
  재귀 호출 한번에 최소 하나의 원소(피벗)은 최종 위치가 정해진다.

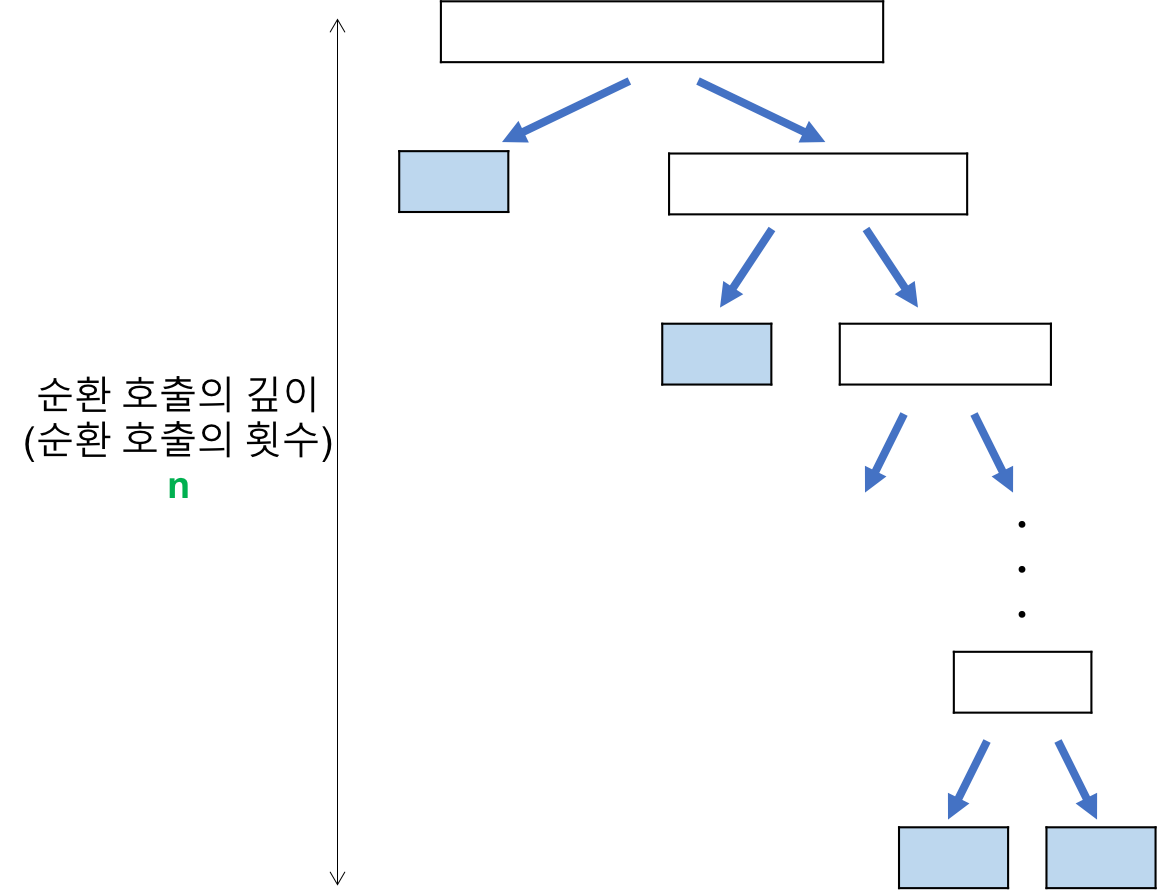
• 시간복잡도 : 최선/평균의 경우 O(n log n). 순환 호출의 깊이가 log n 이고, 각 순환 호출 단계에서 비교 연산이 n번 발생하기 때문에 최선/평균의 경우 n log n이 된다.
  최악의 경우 O(n^2). 배열이 계속 불균형하게 나눠지면(이미 정렬 or 역정렬된 상태면) 순환호출의 깊이가 n이기 때문에 n^2이 된다.

• 공간복잡도 : 재귀 호출로 인해 평균적으로 O(log n)의 메모리를 필요로 한다. 최악의 경우는 O(n)의 공간복잡도를 가진다.

• 장점
  매 단계에서 적어도 1개의 원소가 자기자리를 찾아 갈수록 정렬할 개수가 줄어든다는 점, 불필요한 데이터의 이동을 줄인다는점 때문에 다른 O(n log n) 정렬 알고리즘과 비교했을 때도 가장 빠르다.
  피벗 선택 전략을 바꿔 특정 상황에 맞게 최적화가 가능하다.
  제자리정렬이다.

• 단점
  이미 정렬 or 역정렬 상태의 배열의 경우 오히려 성능이 더 느리다.
  (항상 O(n log n)이 아니기 때문에 안정성이 떨어진다.)
  불안정 정렬이다.
  제자리정렬이지만 재귀 호출에 대한 메모리 상의 스택 공간이 필요하다.
  재귀호출로 인한 오버헤드나 최악의 경우 스택오버플로우의 가능성이 있다.

pivot(피벗) 선택이 중요한 이유

• 퀵정렬에서 worst 케이스는 이미 정렬된 배열이나 역정렬된 배열을 정렬할 때이다.

이미지 출처 : gmlwjd9405 블로그

• 만약 pivot이 가장 첫 원소나 마지막 원소가 되면 각 단계가 원소 1개 / pivot / 나머지 원소 전부 로 쪼개져 분할정복의 이점을 살리지 못하기 때문이다.

• 그래서 이미 정렬된 배열일 경우를 대비해 왼쪽 요소나 오른쪽 요소를 피벗으로 선택하지 않고 가운데 요소를 피벗으로 선택해 위의 최악의 케이스를 피한다.

• 물론 가운데 요소를 피벗으로 선택하는 방법으로도 충분하지 않다. 랜덤으로 선택하는 방법, 랜덤 3값을 뽑아 중간값을 pivot으로 선택하는 방법 등 여러 개선 방법이 존재하는데 이는 다음에 직접 구현해보도록 하겠다.
  참고 사이트

Java로 구현

가운데 값을 pivot으로 정하고 작은 값은 왼쪽, 큰값은 오른쪽으로 스왑해 pivot을 기준으로 정렬한다. 그리고 pivot을 제외한 좌 우 부분배열을 다시 재귀적으로 정렬한다.

public class A_QuickSort {

  public static void quickSort(int[] array) {
    if (array.length >= 2){
      sort(array, 0, array.length-1);
    }
  }

  private static void sort(int[] array, int low, int high){
    if (low >= high) return;

    // 파티션을 나눈다.
    int mid = partition(array, low, high);
    // 나눠진 파티션에서 왼쪽과 오른쪽 부분배열을 다시 정렬한다.
    sort(array, low, mid-1);
    sort(array, mid, high);
  }

  private static int partition(int[] array, int low, int high){
    // low는 왼쪽부터 증가, high는 오른쪽부터 감소
    int mid = (low + high) / 2; // 가운데 값을 피벗으로 정한다.
    int pivot = array[mid];
    while (low <= high){        // low를 계속 증가, high를 계속 감소시켜 만나는 지점까지 while문을 실행
      while (array[low] < pivot) low++; // 피벗보다 작으면 잘 정렬되어있으므로 다음 값으로 low를 넘긴다
      while (array[high] > pivot) high--; // 피벗보다 크면 잘 정렬되어있으므로 이전 값으로 high를 줄인다
      if (low <= high) {              //위의 과정을 거쳐 정렬해야될 low와 high값의 순서가 오면
        // low와 high값을 swap한다.(작은 값을 왼쪽으로, 큰 값을 오른쪽으로 넘기는 과정)
        int tmp = array[low];
        array[low] = array[high];
        array[high] = tmp;
        low++;                        // swap이 되었으므로 다음 값으로 넘어간다.
        high--;
      }
    }
    return low;           // low는 분할된 배열의 경계값을 가진 채로 반환된다.
  }

  public static void main(String[] args) {
    Random random = new Random();
    int[] array = new int[10];
    for (int i = 0; i < array.length; i++) {
      array[i] = random.nextInt(100); // 0~99까지 정수 랜덤
    }

    System.out.print("정렬 전 배열 : ");
    System.out.println(Arrays.toString(array));
    System.out.println("-----------------------------------------");
    quickSort(array);
    System.out.print("퀵정렬 후 배열 : ");
    System.out.println(Arrays.toString(array));
    System.out.println("-----------------------------------------");
  }

}