230713 Today I Learned

오늘은 깊이우선탐색 DFS에 대해 정리해보려 한다.

백트래킹(Backtracking)

모든 경우의 수를 고려하는 알고리즘 중 하나로, 해를 찾는 도중조건을 만족하지 않으면 이전 단계로 돌아가서 다른 가능성을 탐색하는 방법

• 상태 공간을 트리로 나타낼 수 있을 때 유용하다.

• 일종의 트리 탐색 알고리즘

• 방법에 따라서 DFS(깊이 우선 탐색), BFS(너비 우선 탐색), 최선우선탐색이 있다.

• 모든 경우를 고려해야하는 문제는 일반적으로 DFS가 유리하다. BFS를 사용할 경우 큐의 크기가 지나치게 커질 수 있다.

• 하지만 트리의 깊이가 무한대가 될 경우나 미로찾기에서 루프가 발생할 경우처럼 DFS 사용시 탈출이 불가한 문제는 BFS를 사용해야 한다. 최단거리를 구하는 문제도 BFS가 유리하다.

깊이 우선 탐색(DFS)

Depth First Search. 트리나 그래프에서 모든 루트를 완전 탐색하고자 할 때, 최대한 깊숙히 들어가서 확인한 뒤 다른 루트를 찾는 방식이다.

이미지 출처 : 위키피디아

• 막다른 곳, 바닥, 끝까지 가서 길이 없으면 되돌아와 다시 뚫고 들어가는 방식이다.

• 이미 지나간 곳을 체크하면서 중복 순회하지 않도록 해야한다.

• 일반적으로 재귀를 사용해 구현하지만, 단순한 형태의 스택으로도 구현한다. 구조 상 스택오버플로우 문제를 조심해야 한다.

• 단순한 검색 속도 자체는 BFS보다 느리지만 구현이 간단하다. 검색보다는 순회(모든 경로 방문)를 할 경우에 자주 쓰인다.

• 현재 경로의 노드들만 기억하면 되어 저장공간이 덜 필요하다.

• 해를 구하면 탐색이 종료되므로 그 해가 최적해라는 보장이 없다.

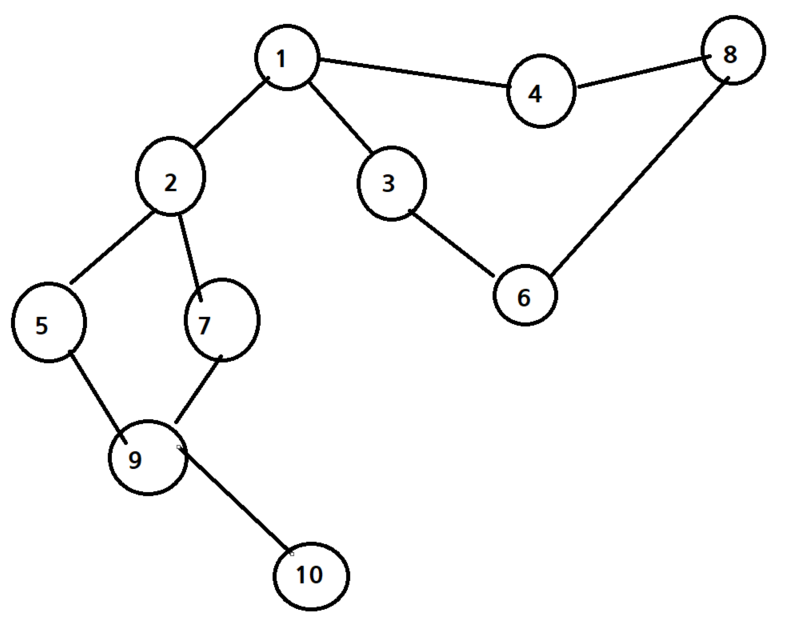
Java로 구현 - 재귀

public class A_DfsR {
  // 노드에 방문한 기록을 boolean 배열로 표현. 0번 노드는 제외한다.
  private static boolean[] checked = new boolean[11];
  // 노드가 연결된 정보를 2차원 배열로 표현
  private static int[][] graph = {{},
      {2,3,4},
      {1,5,7},
      {1,6},
      {1,8},
      {2,9},
      {3,8},
      {2,9},
      {4,6},
      {5,7,10},
      {9}
  };

  // v는 현재 탐색하는 노드
  public static void dfs(int v){
    // 현재 탐색하는 노드는 true로 방문 체크
    checked[v] = true;
    System.out.println(v + "번 노드를 탐색합니다.");

    // 현재 노드에서 연결된 노드가 graph[v]
    for (int i : graph[v]){
      // 체크되지 않은 노드만 방문한다. 재귀로 구현
      if (!checked[i]) dfs(i);
    }
  }

  public static void main(String[] args) {
    int start = 1; // 시작노드
    dfs(start);
  }

}