Today I Learned

오늘은 그래프 구현 방식에 대해 알아보려 한다.

참고 사이트 : born2bedeveloper

그래프 구현 방식

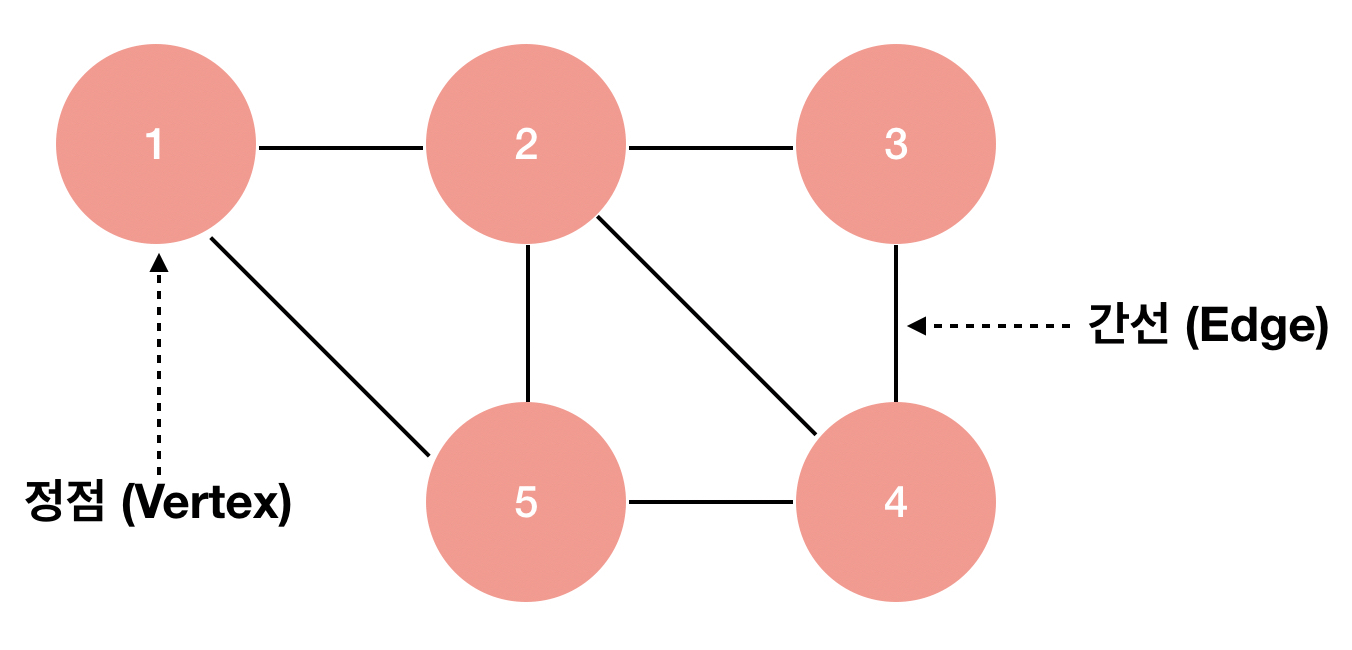
• 그래프 : 정점(vertex/node)과 간선(edge/link)으로 구성된 자료구조. 객체 사이의 관계를 표현할 때 사용된다.

그래프를 구현하기 위해선 정점과 간선을 구현해야 하는데, 인접행렬과 인접리스트 두 가지 방법을 쓸 수 있다.

인접 행렬

간선을 2차원 int[] 배열로 구현하는 방식이다.
정점과 정점의 관계를 1이나 가중치로 표현한다.

• V개의 노드를 표현하기 위해 V^2의 공간이 필요하다.
  따라서 공간복잡도는 O(V^2).

• adj\[3]\[5] == 1 : 3번 정점과 5번 정점이 간선으로 연결되어 있다.

• 구현이 비교적 쉽다.

• 인덱스를 통해 O(1)로 바로 확인이 가능하다.

• 무방향 그래프일 경우 대칭구조다.

• 하지만 한 정점에 연결된 모든 간선을 확인해보기 위해선 1~n까지 다 확인해야하므로 O(n)이 소요되는 단점이 있다. 인접 노드를 찾기위해선 다 확인해봐야한다.

• 노드에 비해 간선이 극히 적은 그래프의 경우 간선 확인에 비효율적이다.

// 무방향 그래프(가중치 x)
// putEdge(graph, x, y)를 하면 x와 y에 둘 다 삽입되는 함수
public static void putEdge(int[][] graph, int x, int y) {
        graph[x][y] = 1; 
        graph[y][x] = 1;
    }

    public static void main(String[] args) {
        int n = 5; // 정점의 개수
        int[][] graph = new int[n+1][n+1]; //index를 1부터 맞추기 위해 n+1로 설정한다.

        putEdge(graph, 1, 2);
        putEdge(graph, 1, 3);
        putEdge(graph, 1, 4);
        putEdge(graph, 2, 3);
        putEdge(graph, 2, 5);
        putEdge(graph, 3, 4);
        putEdge(graph, 4, 5);
    }

인접 리스트

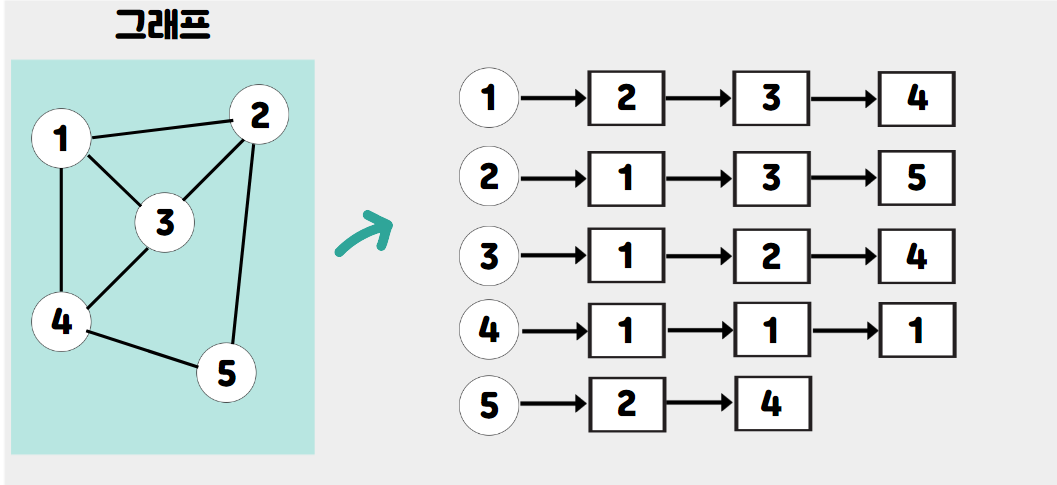
간선을 이중 리스트로 구현하는 방법이다.

• V개의 노드를 표현하기 위해 V개의 리스트에 간선(E)이 E만큼 존재한다.
  따라서, 공간복잡도는 O(V+E)다.

• 위의 특성 덕분에 메모리 공간을 보다 효율적으로 사용한다.

• adj.get(3).contains(5) == true : 3번과 5번 노드가 연결되어 있다.

• 인접한 정점들의 탐색이 빠르다.

• 연결여부를 찾기위해 .contains()로 확인한다면 그 노드에 연결된 노드 수만큼 시간이 소요될 수 있다.

• 한 정점에 연결된 모든 간선 확인하려면 그냥 그 정점의 리스트로 가면 바로 볼 수 있다.

    public static void putEdge(ArrayList<ArrayList<Integer>> graph, int x, int y) {
        graph.get(x).add(y);
        graph.get(y).add(x);
    }

    public static void main(String[] args) {
        int n = 5; // 정점의 개수
        ArrayList<ArrayList<Integer>> graph = new ArrayList<>();

        for (int i = 0; i <= n; i++)
            graph.add(new ArrayList<>()); //각 노드 별 리스트를 만들어준다.
        putEdge(graph, 1, 2);
        putEdge(graph, 1, 3);
        putEdge(graph, 1, 4);
        putEdge(graph, 2, 3);
        putEdge(graph, 2, 5);
        putEdge(graph, 3, 4);
        putEdge(graph, 4, 5);

        print(graph);

    }

비교

• 인접리스트
  메모리 사용이 더 효율적이고, 삽입/삭제가 빈번한 경우 더 유리하다.
  노드에 비해 간선이 희소하다면 인접리스트를 주로 사용한다.

• 인접행렬
  연결여부의 확인이 중요하거나 삽입/삭제가 적은 경우 유리하다.
  노드에 비해 간선이 밀집되어 있다면 인접행렬을 주로 사용한다.