Today I Learned

오늘은 어제 다 마무리 못한 크루스칼 알고리즘에서 사이클 여부를 판단할 때 사용하는 유니온파인드에 대해 정리해보려 한다.

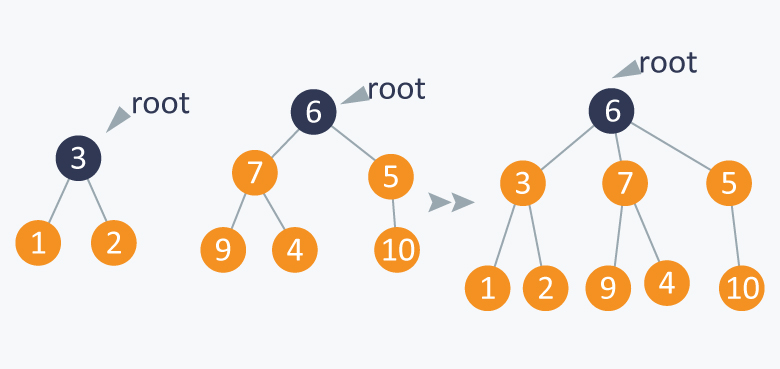
Union-Find

두 노드가 같은 그래프에 속하는지 판단하는 알고리즘

• 서로소 집합, 상호 베타적 집합(Disjoint-Set)이라고도 한다.

• 서로 다른 두개의 집합을 합치는 합집합 Union 연산과 루트노드를 찾는 Find 연산으로 이루어져있다.

• MST 구현 방법 중 크루스칼의 경우 간선을 중심으로 연결하는데 이때 같은 그래프 집합 안의 노드끼리 연결하면 사이클이 만들어져 이를 피해야한다. 이때 같은 그래프인지 판단할 수 있는 알고리즘이 바로 유니온파인드이다.

• find 연산을 통해 각 노드의 부모(루트)노드를 알 수 있고, 같은 루트노드면 같은 그래프이니 연결 시 사이클이 형성된다. 따라서, 다른 루트노드를 가진 노드의 간선만 연결하면 된다.

• 일반적으로 배열을 하나 생성해서 구현한다. 배열의 크기는 노드의 수만큼, 인덱스는 노드의 번호를 의미하고 인덱스에 지정된 숫자가 해당 노드의 루트노드 번호를 의미한다.

• 트리를 사용해 구현하면 좀 더 효율적이다.
  참고 사이트 : gmlwjd9405

구현 코드

간단한 유니온파인드 코드 예시. 여기서 추가적으로 rank 기능을 사용해 트리의 높이를 고려해서 코드를 짤 수도 있다.

1. 부모노드를 저장할 배열을 만든다.

2. 일단 자기자신으로 배열을 초기화 한다.

3. find 메서드는 루트노드(부모노드가 자기 자신)이 발견될 때 까지 재귀함수로 자기 자신을 계속 돌린다.

4. union메서드는 서로의 부모노드를 find 메서드로 비교해서 같지 않을 경우 합치는 메서드다. 같은 그래프에 속하는 노드들끼리 union으로 합쳐둔 상태에서 진행을 하면 된다.

class UnionFind {
    private int[] parent;

    public UnionFind(int size) {
        parent = new int[size];
        for (int i = 0; i < size; i++) {
            parent[i] = i;
        }
    }

    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);

        if (rootX != rootY) {
            parent[rootX] = rootY;
        }
    }
}