Today I learned

오늘은 알고리즘 기법에서 탐색 방법 중 투포인터와 슬라이딩 윈도우 기법에 대해 공부해보려 한다.

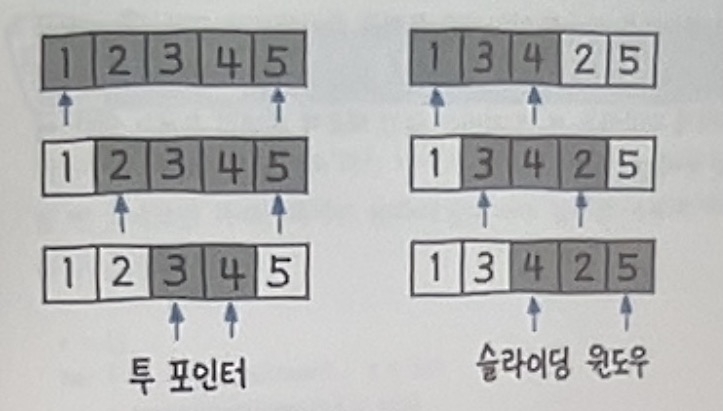
이미지 출처 : @hysong

탐색 기법

• 일반적으로 배열 상에서 특정 조건을 만족하는 두 값을 찾으려면 이중for문으로 O(n^2)의 시간복잡도가 소요된다.

int[] arr = {15,3,11,5,7,1,4};
int target = 12;
int l = arr.length;
for(int i=0;i<l-1;i++){
	for(int j=i+1;j<l;j++){
    	if(arr[i]+arr[j] == target) {
        	System.out.println(i + ", " + j);
        }
    }
}

• 하지만 아래의 기법을 사용해 시간복잡도 O(n)으로 해결할 수 있다.
  (특히 합연산)

투 포인터

배열, 리스트 같은 선형 자료구조에서 두개의 포인터(인덱스)를 사용해 원하는 요소를 찾는 탐색 기법.

• 일반적으로 정렬된 데이터에서 두 개의 포인터를 시작/끝에 두고 탐색을 한다.
  ex) 정렬된 배열에서 두 수의 합이 특정 값이 되는 쌍을 찾으려 할 때.

• 추가적인 메모리 공간을 사용하지 않고도 배열의 특정 값을 효과적으로 찾을 수 있다.

• 배열을 한 번만 순회하므로 O(n)의 시간복잡도를 가진다.

• 일반적으로 양 끝에서 시작하지만 상황에 따라 같은 시작점에서 출발할 수도있다.

• 정렬된 배열에서 효과적으로 작동한다.

• 기본 원리

1. 두 포인터가 배열의 양쪽 끝에서 시작된다.
2. 포인터가 가르키는 값이 타겟보다 작으면 왼쪽 포인터를 오른쪽으로 한 칸 옮긴다.(값 증가)
3. 반대로 타겟보다 크면 오른쪽 포인터를 왼쪽으로 한 칸 옮긴다.(값 감소)
4. 두 포인터가 만날 때까지 이를 반복해 값을 찾는다.

• 코드

int[] arr = {15,3,11,5,7,1,4};
// 투포인터는 정렬을 해야한다.
Arrays.sort(arr);
int target = 12;
int l = arr.length;

int left = 0;
int right = l - 1;

while (left < right) {
    int sum = arr[left] + arr[right];

    if (sum == target) {
        System.out.println(left + " " + right);
        break;
    } else if (sum < target) {
        left++;
    } else {
        right--;
    }
}

슬라이딩 윈도우

배열이나 리스트와 같은 선형 자료구조에서 연속된 요소의 부분집합을 효과적으로 탐색할 때 사용하는 기법.

• 미닫이 문 처럼 배열 안의 부분배열(window)의 크기는 고정되어있지만 배열 상에서 좌표만 움직(slide)인다.

• 포인터 변수가 굳이 2개일 필요가 없다. 고정된 부분배열을 가지면 된다.

• 슬라이딩 윈도우 역시 정렬된 배열에서 효율적이다.

• 모든 부분집합을 순회하지 않아도 되기 때무에 O(n)만에 끝난다.

• 기본 원리

1. 시작과 끝 포인터를 초기화하여 윈도우를 정의한다.
2. 윈도우를 slide하면서 문제의 조건을 만족하는지 확인한다.
3. 조건을 만족하는 윈도우를 찾으면, 이를 기록하고 필요한 경우 더 좋은 해답을 찾기 위해 윈도우를 조절한다.

• 코드
  배열의 연속된 부분 배열 중 합이 주어진 값 k 이상인 가장 작은 부분 배열의 길이를 찾는 문제

public int minSubArrayLen(int k, int[] nums) {
    int minLength = Integer.MAX_VALUE; // 결과 저장
    int sum = 0; // 윈도우 내부의 합
    int left = 0; // 슬라이딩 윈도우의 왼쪽 포인터

    for (int right = 0; right < nums.length; right++) {
        sum += nums[right];

        // 현재 윈도우의 합이 k 이상인 동안 윈도우 크기 줄이기
        while (sum >= k) {
            minLength = Math.min(minLength, right - left + 1);
            sum -= nums[left];
            left++;
        }
    }

    return minLength == Integer.MAX_VALUE ? 0 : minLength;
}

public static void main(String[] args) {
    int[] nums = {2, 3, 1, 2, 4, 3};
    int k = 7;
    System.out.println(new ClassName().minSubArrayLen(k, nums)); // 결과는 2 ([4,3]이 가장 짧은 부분 배열)
}