Today I Learned
오늘은 기존에 풀었던 합승택시요금 문제를 다익스트라가 아닌 플로이드 워셜로 풀어보려한다.
합승택시요금
문제
https://school.programmers.co.kr/learn/courses/30/lessons/72413
TIL #166 참고
풀이 과정
-
다익스트라를 사용할 경우 a,b,s점 총 3번을 돌려야하지만 플로이드 워셜로 한번에 모든경로를 다 탐색하고 결론만 도출하면 더 쉽게 풀 수 있을 것 같았다.
-
INF 를 문제에서 제시한 최대값인 100000원 x n 으로 일단 설정해두고, 플로이드 워셜에 필요한 2차원 배열을 자기자신만 빼고 INF로 초기화해둔다.
-
fares에 있는 요금표를 참고해 graph를 완성한다. 단, 문제에선 1부터 시작하지만 graph는 0부터 시작하므로 시작 인덱스를 -1시켜 맞춰준다.
-
플로이드워셜 메서드를 만들고 graph를 복제한 이차원 배열을 만든다.
-
3중 for문으로 플로이드 워셜 알고리즘을 적용시켜 중간점을 찾아 최소 비용 경로를 2차원 배열에 기록한다.
-
완성된 플로이드 워셜 2차원 배열을 for문으로 탐색해 비용이 가장 최소가 되는 지점을 찾아 그 비용을 반환한다.
구현 코드
import java.util.*;
class Solution {
static int INF;
public int[][] floydWarshall(int[][] graph, int n){
int[][] dist = new int[n][n];
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
dist[i][j] = graph[i][j];
}
}
for(int m=0; m<n; m++){
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
if(dist[i][j] > dist[i][m] + dist[m][j]){
dist[i][j] = dist[i][m] + dist[m][j];
}
}
}
}
return dist;
}
public int solution(int n, int s, int a, int b, int[][] fares) {
INF = 100000*n;
int answer = INF;
int[][] graph = new int[n][n];
for(int i=0; i<n; i++){
Arrays.fill(graph[i], INF);
graph[i][i] = 0;
}
for(int[] fare : fares){
graph[fare[0]-1][fare[1]-1] = fare[2];
graph[fare[1]-1][fare[0]-1] = fare[2];
}
int[][] dist = floydWarshall(graph, n);
for(int i=0; i<n; i++){
answer = Math.min(answer, dist[a-1][i] + dist[b-1][i] + dist[i][s-1]);
}
return answer;
}
}다익스트라 vs 플로이드 워셜
-
플로이드 워셜 효율성 테스트 결과

-
다익스트라 효율성 테스트 결과
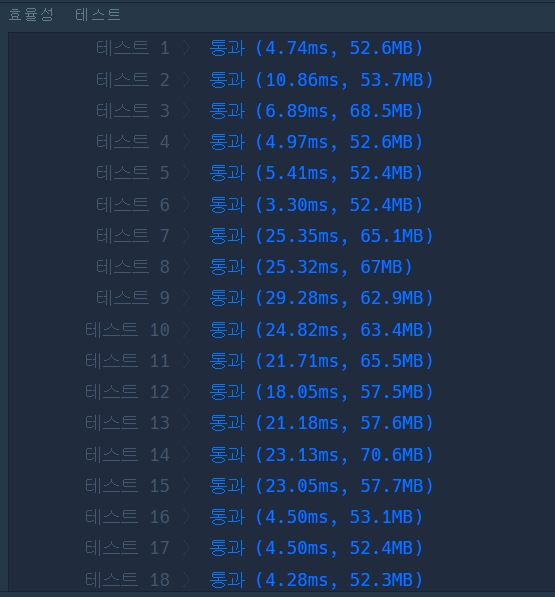
비교해보면 역시 전반적으로 다익스트라가 훨씬 빠르다. 플로이드 워셜은 3중 for문으로 시간복잡도가 O(v^3)인데다가 모든 경로를 다 탐색하기때문에 느릴수밖에 없다.
하지만 47줄(플) vs 84줄(다)로 훨씬 구현이 쉽고 간단하며 가독성이 좋다. 플로이드 워셜로 효율성 테스트를 통과하기 어려워 코테에선 잘 쓸 수 있을진 모르겠지만 간단하게 최단 경로를 탐지하기 좋다는 장점이 확실하긴 하다.
