Today I Learned
오늘도 랜덤한 문제를 풀어봤다. 그리디 알고리즘쪽이 안그래도 약하다고 생각했는데 그 쪽 문제가 나와서 좋았다. 하지만 문제 자체는 딱히 좋은 문제라고는 생각하지 않는다. 어떤 알고리즘적 사고방식을 사용하는 문제라기 보단 수학적으로 이 문제에만 적용 가능한 특정 방법을 찾아서 구현한 문제로 보인다.
기지국 설치
문제
N개의 아파트가 일렬로 서있다. 현재 기지국이 설치된 아파트의 위치를 나타내는 배열 stations, 기지국 당 커버 범위 w 가 주어질 때 모든 아파트를 커버할 수 있는 추가 기지국의 최소 개수를 구하라.

풀이 과정
boolean 배열 사용
-
boolean 배열 avail을 만들어 현재 통신이 가능한 아파트를 true로 뒀다.
-
for문을 돌면서 stations에 있는 아파트를 기준으로 자기 자신과 +-w 범위의 아파트들을 true로 둔다.
-
if 문을 사용해 index 초과가 나지않도록 했다.
-
avail boolean배열을 처음부터 순회하면서 false인 아파트를 기준으로 +w 지점에 기지국을 설치하면 그곳을 기준으로 +-w 범위까지 커버가 되므로 가장 효율적이라고 판단,
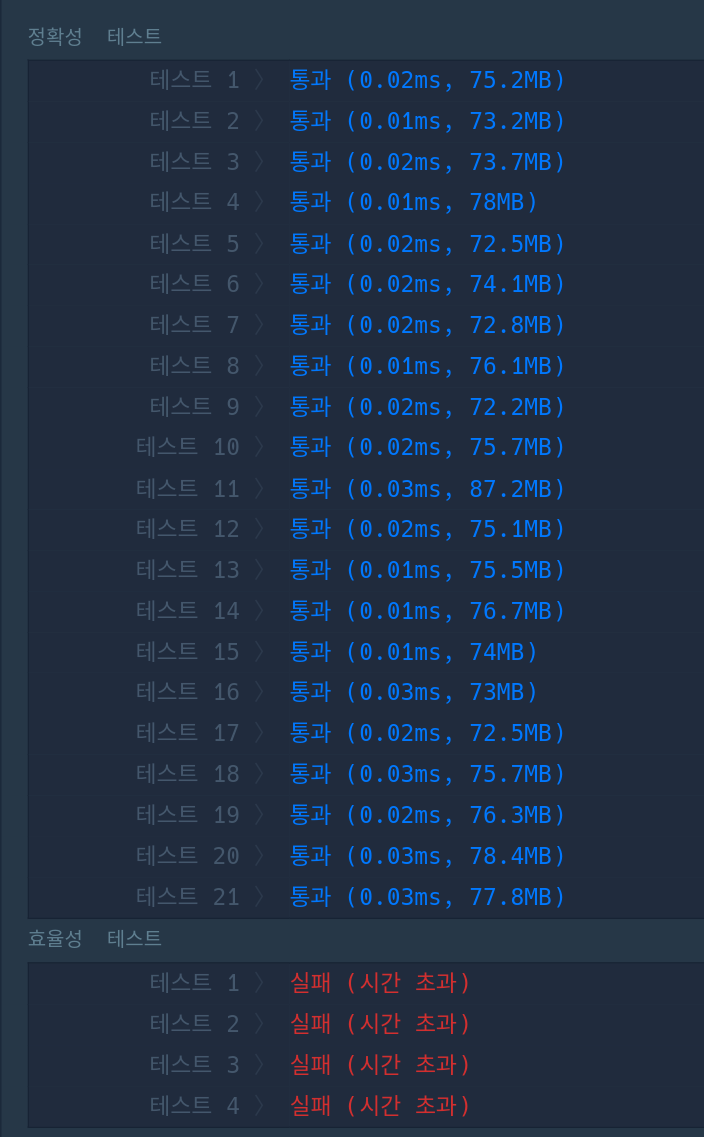
- 0.0x ms 정도라서 시간복잡도는 괜찮을꺼라 생각했는데 효율성 테스트에서 계속 실패했다.
아마 n의 값이 커서 코드상 비효율이 발생한 것 같아 아예 boolean 배열도 안쓰고 새로 구현해보고자 했다.
배열 없이 시간복잡도 단축 풀이
-
발상 자체는 위와 크게 차이는 없다. 다만 배열 자체를 아예 만들지 않고, while문 안에서 인덱스만 가지고 O(n)보다 시간복잡도가 적게, 즉 한번 이내에 순회를 통해 모든 답을 구할 수 있게 짰다.
-
우선 stations 배열을 순회할 인덱스 변수를 하나 할당하고, 아파트도 1부터 순회할 인덱스를 하나 만든다.
-
아파트가 n까지 있으므로 그가지 while문 한계를 둔다.
현재 체크하는 아파트가 기지국의 커버 범위 안이라면, stIdx를 다음으로 넘기고, 아파트는 기지국의 오른쪽 커버범위 다음인 stations[stIdx] + w + 1로 넘긴다. -
현재 체크하는 아파트가 기지국의 커버 범위에 없다면 기지국을 새로 설치해야 한다. 하지만 바로 설치하는 것 보다는 현재 위치에서 +w 된 곳에 설치한다면 양옆으로 2w를 커버하기 때문에 가장 효율적일 것이다. 그러므로 그 곳에 기지국 설치를 하나 하고(answer++), 해당 기지국 커버 범위 바로 뒤로 아파트 번호를 넘긴다. (apt += 2 w + 1;)
구현 코드
boolean 배열 사용 코드(효율성 fail)
class Solution {
public int solution(int n, int[] stations, int w) {
int answer = 0;
boolean[] avail = new boolean[n+1];
avail[0] = true;
for(int station : stations){
avail[station] = true;
for(int i=1; i<=w; i++){
if(station+i<=n) avail[station+i] = true;
if(station-i>=1) avail[station-i] = true;
}
}
int i = 1;
while(i<=n){
if(avail[i] == true) {
i++;
continue;
}
answer++;
for(int j=0; j<=2*w; j++){
if(i+j<=n) avail[i+j] = true;
}
i += 2*w + 1;
}
return answer;
}
}개선 코드
class Solution {
public int solution(int n, int[] stations, int w) {
int answer = 0;
int stIdx = 0; // stations 배열의 기지국 인덱스
int sl = stations.length;
int apt = 1; // while문 안에서 순회중인 아파트 번호
while(apt<=n){
// 현재 아파트가 기존 기지국 커버 범위 안일 때
if(stIdx<sl && apt >= stations[stIdx]-w){
apt = stations[stIdx]+w+1;
stIdx++;
} else {
// 기지국 커버 범위 밖이면 apt+w에 기지국을 설치하고 그 범위는 apt+2w까지 간다.
answer++;
apt += 2*w+1;
}
}
return answer;
}
}비교
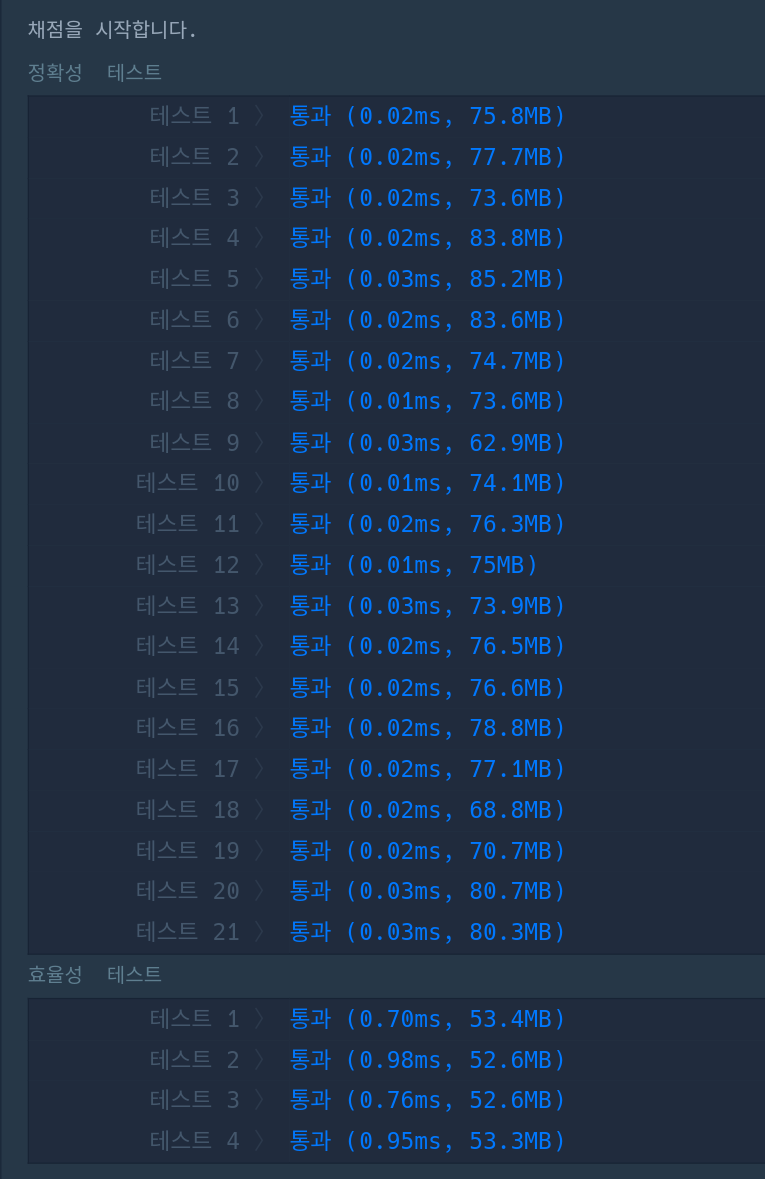
- gpt를 이용해 두 코드를 비교해보니 중복 연산이 줄어 개선된 코드가 더 효율적으로 보인다.
성능 비교:
시간적 성능: 두 코드 모두 시간 복잡도가 O(n)으로 동일하게 보입니다. 그러나 두 번째 코드는 불필요한 중복 연산이 없기 때문에 실제 실행 시간은 첫 번째 코드보다 빠르게 작동할 것입니다.
공간적 성능: 첫 번째 코드는 O(n)의 공간을 사용하는 반면, 두 번째 코드는 O(1)의 공간만을 사용합니다. 따라서 두 번째 코드가 공간적 성능 면에서 훨씬 우수합니다.
결론: 두 번째 코드가 첫 번째 코드보다 효율적입니다. 첫 번째 코드는 불필요한 배열을 사용하여 메모리를 더 많이 사용하며, 중복 연산이 있어서 실제 실행 시간이 더 길어질 수 있습니다.
