Today I Learned

오늘은 Leetcode에서 문제를 풀다가 개념을 알게된 카데인 알고리즘에 대해 공부해보았다.

참고 사이트 : vdongbin

Kadane Algorithm

배열에서 연속된 부분 배열의 최대 합을 찾는 데 사용되는 효율적인 알고리즘

• 동적 계획법(DP)의 일종으로, 각 단계에서 현재 위치의 최대 부분 배열 합을 저장하면서 배열을 순회하는 방식이다.

• 주로 배열 또는 리스트에서 연속된 부분 배열의 최대 합을 찾는 데 사용된다.

• brute force라면 O(n^2)이 걸리겠지만, 카데인 알고리즘의 시간 복잡도는 O(n)으로 간단하게 찾을 수 있다.

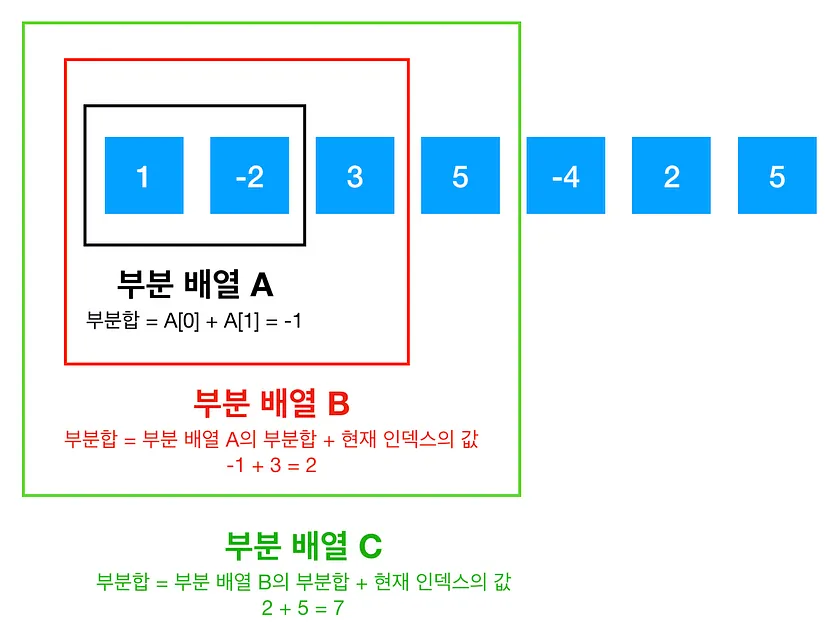
• 핵심은 각각의 최대 부분합은 이전 최대 부분합이 반영된 것이다.

• 각각의 부분배열의 합은 이전 부분배열의 합에 현재의 인덱스 값을 더한 값이므로, 이전 인덱스가 갖고 있는 최대 부분합을 이용해 현재 인덱스의 최대 부분합을 구하는 것이다.

예시

maxEndingHere 변수는 현재 위치에서 끝나는 부분 배열의 최대 합을 나타내고, maxSoFar 변수는 현재까지 발견한 최대 부분 배열의 합이다. 배열을 순회하면서 각 위치에서 maxEndingHere를 갱신하고, maxSoFar를 최신의 최대 값으로 유지한다.

public class A_KadaneAlgorithm {
  public static void main(String[] args) {
    int[] array = {-2, -3, 4, -1, -2, 1, 5, -3};

    int max = Integer.MIN_VALUE;
    // Brute Force
    for (int i = 0; i < array.length; i++) {
      int sum = 0;
      for (int j = i; j < array.length; j++) {
        sum += array[j];
        max = Math.max(max, sum);
      }
    }
    System.out.println("완전 탐색으로 구한 최대 연속 부분 배열의 합: " + max);

    // 카데인 알고리즘
    int maxEndingHere = array[0];
    int maxSoFar = array[0];

    for (int i = 1; i < array.length; i++) {
      maxEndingHere = Math.max(array[i], maxEndingHere + array[i]);
      maxSoFar = Math.max(maxSoFar, maxEndingHere);
    }

    System.out.println("카데인으로 구한 최대 연속 부분 배열의 합: " + maxSoFar);
  }
}