Today I Learned
해시맵을 사용해 문제 하나를 풀었다. 해시에 대해서는 알고있지만 제대로 정리해본 적은 없어 사용한 김에 정리를 해두고 확실히 알고 넘어가보려 한다.
해시
특정 데이터를 고정된 길이의 문자열로 변환하는 과정
이렇게 변환된 문자열은 고유한 데이터를 나타내며, 이를 통해 데이터를 식별하고 검색할 수 있다.

해시 함수
입력 데이터를 해시 값으로 변환하는 데 사용되는 함수
-
고유한 해시 값 생성: 데이터의 특정 특성을 활용해 해시 값을 생성하며, 입력 데이터가 조금만 다르더라도 다른 해시값을 생성한다.
동일한 입력에 대해선 항상 동일한 해시값을 반환한다. -
빠른 연산: 해시 함수는 빠르게 실행되어야 하며, DB나 자료구조에서 빠른 검색을 가능하게 한다.
일반적으로 삽입, 검색, 제거에 최악의 경우에도 시간복잡도가 O(1)이다. -
고른 분포: 좋은 해시 함수는 입력 데이터를 고르게 분포시켜야 한다.(simple uniform hashing) 해시 충돌을 최소화하고 효율적인 자료구조의 사용을 가능하게 한다.
해시 충돌(Collision)
- 두 개의 다른 key가 동일한 hash값을 가질 경우 충돌이 발생한다.
해시 함수가 생성하는 해시값은 고유해야하지만, 입력 데이터가 많아지면 중복이 일어나 충돌이 발생할 수 있다.
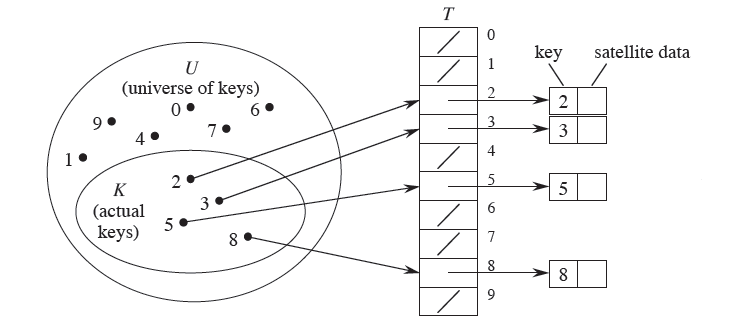
-
key와 동일한 크기의 버킷을 가진 해시 테이블을 Direct-address Table이라 한다. 키의 개수와 테이블의 크기가 같기 때문에 충돌문제가 발생하지 않는다.
-
하지만 일반적인 상황처럼 실제 사용하는 키가 적을 경우에는 잠재적인 키 만큼 버킷 크기를 잡는 것은 메모리의 낭비가 발생한다.
-
따라서, 일반적인 경우 키 개수보다 적은 버킷을 운용하고, 해시 충돌이 발생할 수 밖에 없다.
해결방법

-
체이닝(Chaining)
중복된 해시값이 발생하면 해당 슬롯을 연결리스트로 저장한다.
충돌은 피할 수 없지만 충돌이 발생해도 효율적으로 데이터를 저장할 수 있다.
미리 충돌을 대비해 공간을 잡아둘 필요가 없다.
하지만 연결이 많이 되면 검색 효율이 낮아진다. -
개방주소법(Open Addressing)
충돌 발생 시 해시함수로 얻은 주소가 아니라 다른 빈 공간에 데이터를 저장한다. 데이터 삭제시 체이닝에 비해 비효율적이다.
- 빈 공간을 찾는 방법
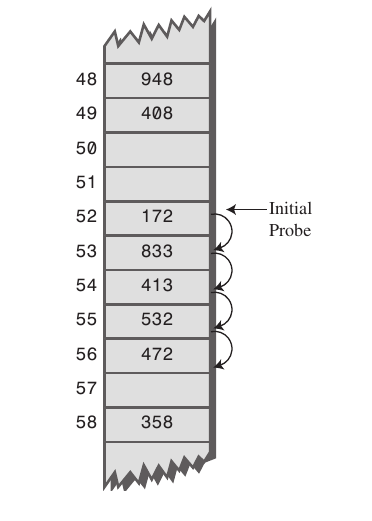
2-1. 선형 탐색(Linear Probing)
충돌이 발생하면 고정된 폭으로 건너뛰어 빈 공간을 찾아 저장한다.
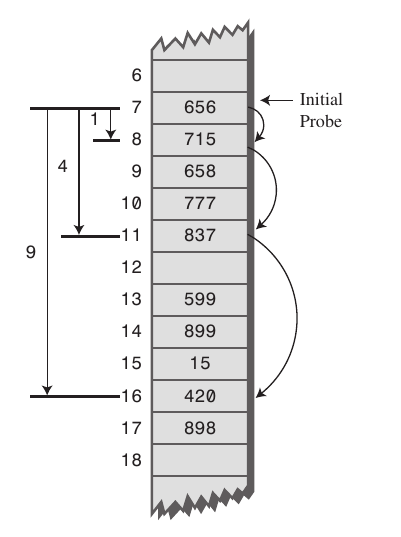
2-2. 제곱 탐색(Quadratic Probing)
고정 폭이 아닌 일정 간격(ex.제곱수 간격, 1->2->4->16)으로 칸을 건너 뛰면서 빈 공간을 찾는다.
2-3. 이중 해싱(Double Hashing)
두개의 해시 함수를 사용해 충돌이 발생하면 다른 해시함수로 다시 해시 값을 만들어 낸다. 또 다른 저장공간 없이 해시 테이블 내에서 데이터의 저장과 처리가 가능하다.
HashMap in Java
-
자바에서는 HashTable 클래스가 HashMap보다 먼저 등장한 자료구조이지만, 둘 다 Map 인터페이스를 구현하기 때문에 제공하는 기능은 비슷하다.
-
HashMap은 충돌방지로 Seperate Chaining 기법을 사용한다. remove()에서 개방주소법 보다 유리하기 때문이다.
-
HashMap은 보조 해시 함수를 사용해 HashTable에 비해 충돌이 덜 발생할 수 있어 성능상 이점이 있다.
-
HashMap은 기본적으로는
동기화를 지원하지 않는다. 동기화 처리 비용에 이점이 있기 때문에 싱글 쓰레드 환경에서 성능상 이점이 있다. -
하지만 멀티쓰레드 환경이라고 해서 HashTable을 사용하지는 않는다. 레거시 클래스이고, 오래된 라이브러리에서 호환성을 유지하기 위해 남아있을 뿐이다. 멀티쓰레드 환경에서도 좀 더 현대적이고 안전한 Map 구현체인 ConcurrentHashMap을 사용하는 것이 낫다.
