Today I Learned
오늘은 ML LifeCycle 2주차의 마지막날.
강의를 이미 다 수강했기 때문에 간단한 복습을 하고 머신러닝 기초수학 책으로 공부를 했다.
강의 복습
선형회귀 그래프 그리기
- numpy와 plt 사용해 데이터 찍기
D1 = np.array([[1.0, 1.2, 3, 4, 5, 6],
[1.5, 3, 2.3, 5.3, 3.8, 5.5]]) # x좌표
D2 = np.array([[-0.6, 1.0, 1.2, 3, 4, 5, 6],
[2.9, 1.5, 3, 2.3, 5.3, 3.8, 5.5]]) # y좌표
fig, (ax1, ax2) = plt.subplots(1,2,sharex=True, sharey=True) # 두 개의 서브플롯을 가로로 배치하고, x와 y축을 공유하는 플롯 생성
fig.set_size_inches((15,6)) # 전체 플롯의 크기를 15인치 x 6인치로 설정
ax1.plot(D1[0], D1[1], 'ko', markersize=10) # D1 데이터의 첫 번째 서브플롯을 'ko' (검은색 원) 마커로 표시, 마커 크기는 10
ax1.set_xlim([-1,7]) # 첫 번째 서브플롯의 x축 범위를 -1에서 7로 설정
ax1.set_ylim([1,6]) # 첫 번째 서브플롯의 y축 범위를 1에서 6으로 설정
ax1.set_title('D1', fontsize=18) # 첫 번째 서브플롯의 제목을 'D1'로 설정하고, 글꼴 크기를 18로 지정
ax2.plot(D2[0], D2[1], 'ko', markersize=10) # D2 데이터를 같은 형식으로 두 번째 서브플롯에 표시
ax2.set_xlim([-1,7]) # 두 번째 서브플롯의 x축 범위를 -1에서 7로 설정
ax2.set_ylim([1,6]) # 두 번째 서브플롯의 y축 범위를 1에서 6으로 설정
ax2.set_title('D2', fontsize=18) # 두 번째 서브플롯의 제목을 'D2'로 설정하고, 글꼴 크기를 18로 지정
plt.show() # 플롯을 화면에 표시
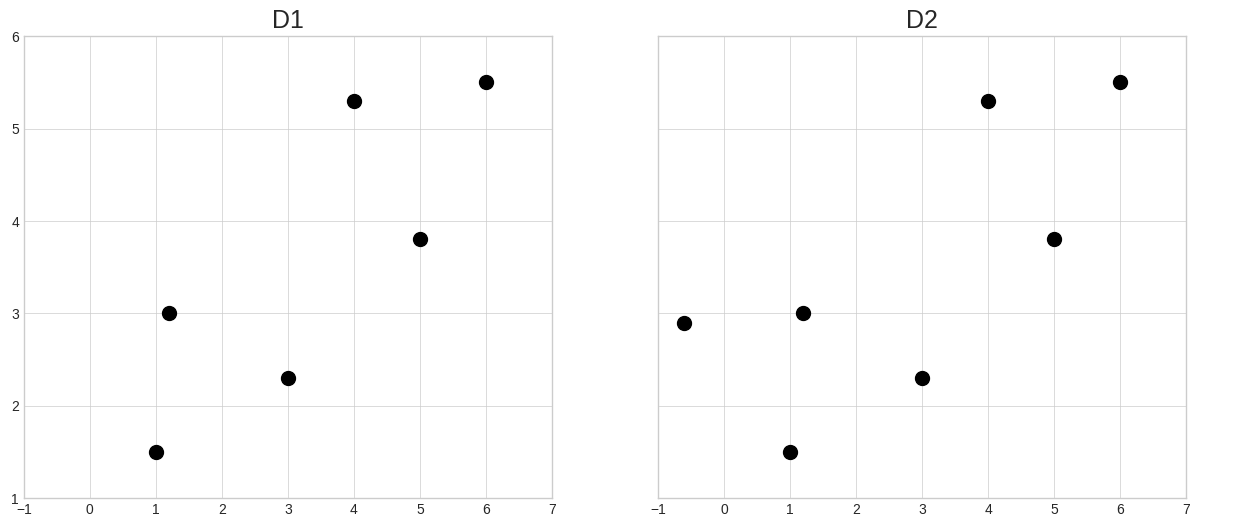
- ㄱ
def machine_learning(D):
"""
선형회귀 알고리즘을 사용하여 최적의 직선을 계산
D : (2,N)의 어레이로 1행에는 데이터의 x좌표
2행에는 데이터의 y좌표가 저장
"""
# 데이터의 개수를 N에 할당
N = D.shape[1]
# 1열에 1, 2열에 데이터의 x좌표를 가지는 행렬
# X: (N,2), y: (N,)
X = np.c_[np.ones(N), D[0]]
y = D[1]
# normal equation
w = np.linalg.solve(np.dot(X.T, X), np.dot(X.T, y))
return w
def more_clever(D):
"""
첫점과 끝점을 연결하는 직선을 계산
D : (2,N)의 어레이로 1행에는 데이터의 x좌표
2행에는 데이터의 y좌표가 저장
"""
first, last = D[:,0], D[:,-1]
w1 = (last[1]-first[1]) / (last[0]-first[0])
w0 = -w1*first[0] + first[1]
return (w0, w1)
def f(x, w):
"""
주어진 w를 사용하여 직선 f(x) = w[1]*x + w[0]의 값을 계산
"""
return w[1]*x + w[0]# D1에 대해서 w[1]*x + w[0]에서 w[0], w[1]을 구함
w_ml_d1 = machine_learning(D1)
w_mc_d1 = more_clever(D1)
# D2에 대해서 w[1]*x + w[0]에서 w[0], w[1]을 구함
w_ml_d2 = machine_learning(D2)
w_mc_d2 = more_clever(D2)
x = np.linspace(-1, 7, 100)
fig, (ax1, ax2) = plt.subplots(1, 2, sharex=True, sharey=True)
fig.set_size_inches((15,6))
ax1.xaxis.set_tick_params(labelsize=18)
ax1.yaxis.set_tick_params(labelsize=18)
ax1.set_xlabel('x', fontsize=25)
ax1.set_ylabel('y', fontsize=25)
ax1.grid(False)
ax2.xaxis.set_tick_params(labelsize=18)
ax2.yaxis.set_tick_params(labelsize=18)
ax2.set_xlabel('x', fontsize=25)
ax2.set_ylabel('y', fontsize=25)
ax2.grid(False)
ax1.plot(D1[0], D1[1], 'ko', markersize=10)
ax1.plot(x, f(x, w_ml_d1), c='k', lw=2, label='machine learning')
ax1.plot(x, f(x, w_mc_d1), '--', c='k', lw=2, label='more clever')
ax1.set_xlim([-1,7])
ax1.set_ylim([1,6])
ax1.legend(fontsize=18)
ax2.plot(D2[0], D2[1], 'ko', markersize=10)
ax2.plot(x, f(x, w_ml_d2), c='k', lw=2, label='machine learning')
ax2.plot(x, f(x, w_mc_d2), '--', c='k', lw=2, label='more clever')
ax2.set_xlim([-1,7])
ax2.set_ylim([1,6])
ax2.legend(fontsize=18)
plt.show()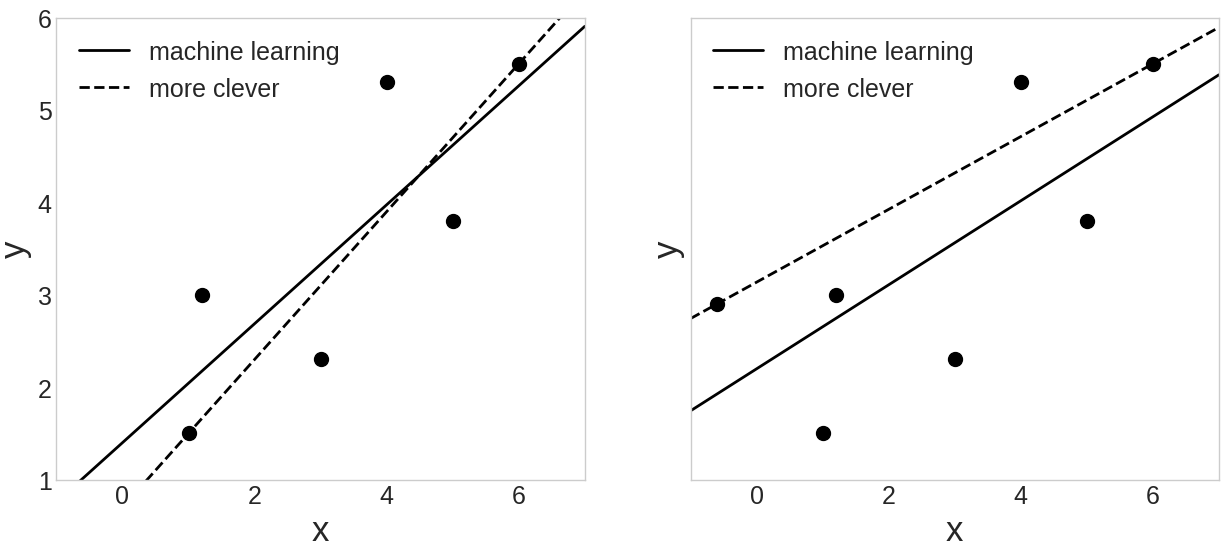
-
단순히 끝점끼리 잇는 more_clever가 더 설명을 못한다.
-
y = f(x,w) = +
-
머신러닝은
숨어있는 입력과 출력의 관계를 찾는 과정 -
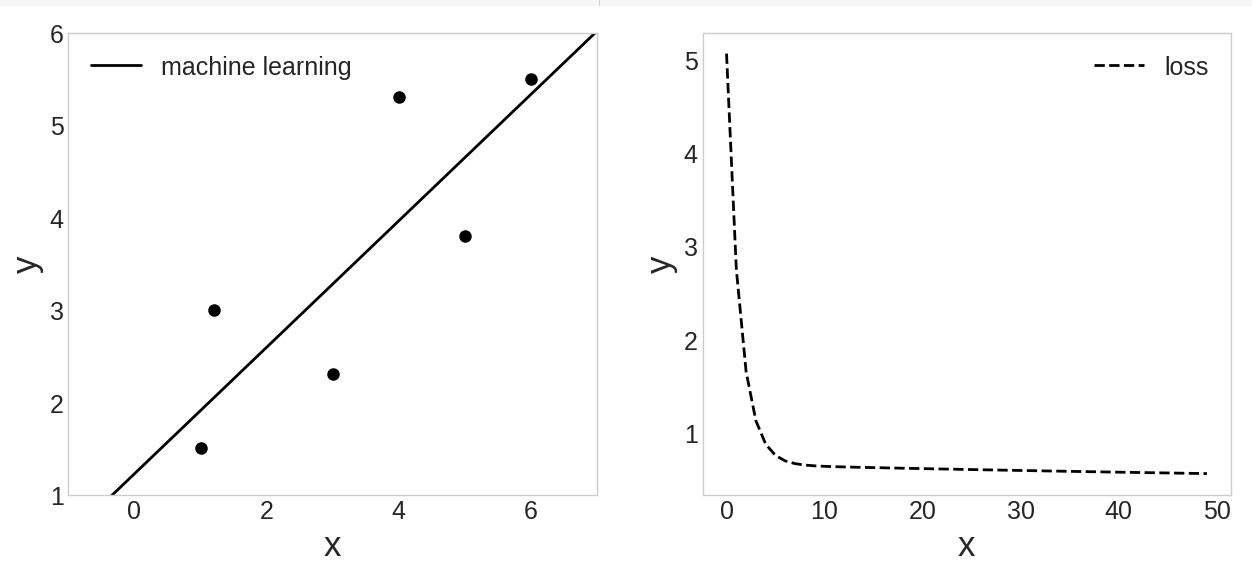
loss 측정 그래프
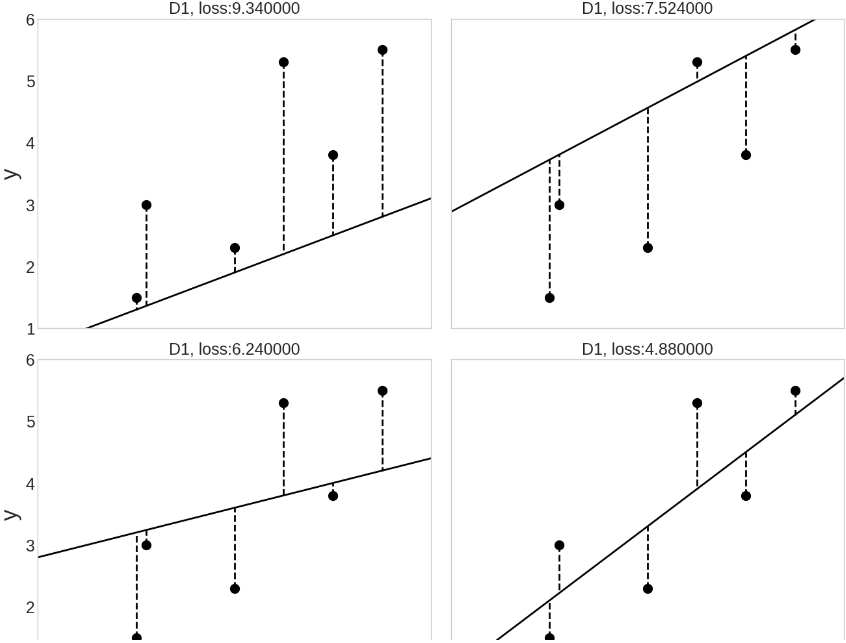
-
150회만 학습
num_iters = 150 # 학습 횟수
alpha = 0.02
np.random.seed(2)
w = np.random.randn(2) # 랜덤하게 초기화
N = D1.shape[1]
ws, L = [], []
# 1열에 1, 2열에 데이터의 x좌표를 가지는 행렬
# X: (N,2), y: (N,)
X = np.c_[np.ones(N), D1[0]]
y = D1[1]
# 경험 E를 반복하면서 태스크 T를 개선
for i in range(num_iters) :
# grad L
c = (1/N) * np.dot(X.T, np.dot(X, w) - y)
# 안전장치 grad L을 이용해서 w를 수정
w -= alpha * c
# w가 변화되는 과정을 저장
ws.append(w)
# 손실을 계산
L.append( ((np.dot(X, w) - y)**2).sum()/(2*N) )
x = np.linspace(-1, 7, 100)
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches((15,6))
ax1.xaxis.set_tick_params(labelsize=18)
ax1.yaxis.set_tick_params(labelsize=18)
ax1.set_xlabel('x', fontsize=25)
ax1.set_ylabel('y', fontsize=25)
ax1.grid(False)
ax2.xaxis.set_tick_params(labelsize=18)
ax2.yaxis.set_tick_params(labelsize=18)
ax2.set_xlabel('x', fontsize=25)
ax2.set_ylabel('y', fontsize=25)
ax2.grid(False)
ax1.plot(D1[0], D1[1], 'ko', markersize=8)
ax1.plot(x, f(x, w), c='k', lw=2, label='machine learning')
ax1.set_xlim([-1,7])
ax1.set_ylim([1,6])
ax1.legend(fontsize=18)
ax2.plot(L[:50], '--', c='k', label='loss')
ax2.legend(fontsize=18)
plt.show()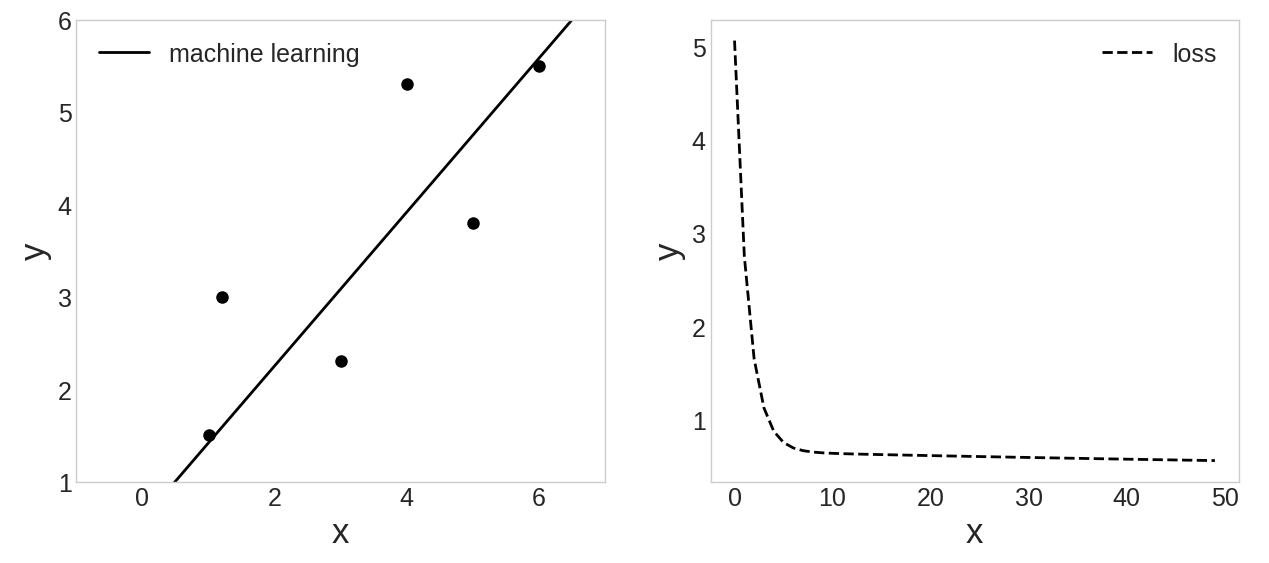
- 500회 학습 (num_iters = 500)
피어세션
-
앞으로 피어세션때 어떻게 해야할 지 방향성에 대해서 논의했다.
우선 코테 주에 2문제씩(프로그래머스 1, leetcode 1) 풀어보기
그리고 강의 들으면서 모르는 부분 화두 던져서 토의해보고, 없으면 질의응답 보면서 완벽히 이해하고 넘어가기. -
attention과 self-attention의 차이?
attention은 인코더의 출력을 기반으로 디코더가 다음 상태를 생성할때 사용되므로 timestep이 필요하다. 하지만 self-attention은 동일한 시퀀스 내에서 요소들 간의 관계를 학습하는 데 사용되는데 단어 한 개에 대하여 모든 단어의 Attention Score를 구하는 구조라서 time step이 필요없다. 따라서 병렬 처리가 가능하다.
멘토링
- Bayes, 빈도주의vs베이지안, 가능도, MLE vs MAP, EM 알고리즘에 대해 배웠는데 이 부분은 정리가 아직 덜 돼서 정리하고 포스팅 올리는게 좋을 것 같다.
회고
-
미리 강의를 열심히 들어두니 여유 시간이 생겨서 추가적인 공부를 할 수 있었다.
-
내일부터 시작하는 3주차도 강의를 부지런하게 들어두면 좋을 것 같다.
