Hough Transform(허프 변환)과 직선 검출

Hough Transform (허프 변환)

이미지에서 직선, 원, 또는 다른 기하학적 형태(shape)를 찾는데 사용되는 CV 알고리즘

이 직선들을 “허프 공간(Hough space)”이라는 파라미터 공간에서 표현한다. 허프 공간에서는 직선을 보통 $(\rho, \theta)$ 좌표를 사용하여 표현한다. 여기서 $\rho$는 원점에서 직선까지의 거리를 나타내고, $\theta$는 수직선과 직선 사이 각도를 나타낸다. 이미지의 각 edge 픽셀에 대한 모든 가능한 $(\rho, \theta)$ 값을 계산하여 허프 공간에 투표(vote)를 한다. 많은 투표를 받은 $(\rho, \theta)$ 값을 이미지에 나타나는 강한 직선으로 취급한다.

직선은 흔히 $y=mx+c$ 형태의 일차 방정식으로 표현될 수 있다. 그러나 이러한 방정식은 수직선의 기울기가 무한대가 되는 경우를 다루기 어렵다. 허프 변환은 이러한 점을 고려하여 $\rho, \theta$ 를 사용한 극좌표계를 사용한다. 직선의 극좌표계 표현은 다음과 같다.

$\rho = xcos(\theta)+ysin(\theta)$

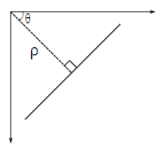
앞서 언급되었듯, $\rho$는 원점에서 직선까지의 거리를 나타내고, $\theta$는 수직선과 직선 사이 각도(반시계방향)를 나타낸다. 그러면 이제 모든 직선을 $\rho, \theta$ 이 두 매개변수로 표현할 수 있다. 이러한 매개변수 값은 2D 배열(Hough space)을 통해 저장된다. $\rho$는 행(row), $\theta$는 열(column)을 나타낸다.

배열의 크기는 얻고자 하는 정확도(accuracy)에 따라 달라질 수 있는데 일반적으로 1°가 사용되고, 그러면 총 180개($\theta$:0~180°)의 열이 필요하게 된다.

N*N 픽셀 이미지에 대한 허프 변환을 예로 들어보자. 허프 변환을 수행하기 위해서는 먼저 edge 검출이 필요하므로, Canny Edge와 같은 알고리즘을 사용하여 edge 픽셀 이미지를 얻는다.

그러면 $\rho$ 값의 최대 범위는 이미지 대각선 길이 $\sqrt{N^2+N^2}$ 로 나타낼 수 있다. $\theta$ 값의 범위는 앞서 말한 대로 0~180° 사잇값이다. 각 edge 픽셀에 모든 가능한 $\theta$ 값에 대한 $\rho = xcos(\theta)+ysin(\theta)$를 계산하고, 2D 배열인 Hough space(허프 공간)에서 해당하는 $(\rho, \theta)$ 값을 증가시킨다. 이 누적 과정이 끝나면, 허프 공간 내에서 가장 높은 값을 가진 셀들의 $(\rho, \theta)$ 값을 이미지 내 직선 매개변수로 해석하게 된다.

Hough Transform의 구현 (직선 검출하기)

Hough Transform을 이용해서 이미지 내 직선을 검출하여 보자. (python, opencv 구현 코딩)

Hough Transform (Standard)

# 표준 허프 변환
lines_standard = cv2.HoughLines(edges, 1, np.pi/180, 132)

"""
cv2.HoughLines() parameters
1. edges -> edge pixel image (input image name)
2. 1 -> 거리 해상도(rho, generally use 1 pixel)
3. np.pi/180 -> 각도 해상도. 위에서 설명한 
								정확도에 따른 배열 크기 값(theta, generally use 1°)
4. 132 -> threshold value (직선 결정을 위한 최소 투표 수)
"""

# 표준 허프 변환으로 찾은 직선 그리기
if lines_standard is not None:
    for line in lines_standard:
        rho, theta = line[0]
        a = np.cos(theta) # θ에서의 cosine 값
        b = np.sin(theta) # θ에서의 sin 값
        x0 = a * rho # 직선과 x축이 만나는 점의 x 좌표
        y0 = b * rho # 직선과 y축이 만나는 점의 y 좌표 
        x1 = int(x0 + 1000 * (-b)) 
		# x1 : 직선 위의 한 점으로부터 직선을 따라 왼쪽으로 1000 픽셀 떨어진 점의 x 좌표
        y1 = int(y0 + 1000 * (a))
		# y1 : 동일한 점으로부터 위쪽으로 1000 픽셀 떨어진 점의 y 좌표
        x2 = int(x0 - 1000 * (-b))
		# x2 : 직선 위의 한 점으로부터 직선을 따라 오른쪽으로 1000 픽셀 떨어진 점의 x 좌표
        y2 = int(y0 - 1000 * (a))
		# y2 : 동일한 점으로부터 아래쪽으로 1000 픽셀 떨어진 점의 y 좌표
        cv2.line(image, (x1, y1), (x2, y2), (0, 0, 255), 2)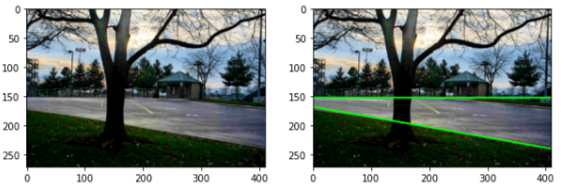

Probabilistic Hough Transform

확률적 허프 변환은 표준 허프 변환의 변형으로, 모든 픽셀을 사용하는 것이 아닌, 임의의 픽셀의 부분 집합만을 사용하여 계산 효율성을 개선하였다.

# 확률적 허프 변환
lines_probabilistic = cv2.HoughLinesP(edges, 1, np.pi/180, 132, 
										minLineLength=100, maxLineGap=10)

"""
cv2.HoughLinesP() parameters
1. edges -> edge pixel image (input image name)
2. 1 -> 거리 해상도(rho, generally use 1 pixel)
3. np.pi/180 -> 각도 해상도. 위에서 설명한 
								정확도에 따른 배열 크기 값(theta, generally use 1°)
4. 132 -> threshold value (직선 결정을 위한 최소 투표 수)
5. 100 -> minLineLength (직선으로 감지되는 최소 길이, 이보다 짧으면 무시)
6. 10 -> minLineGap (직선으로 감지되기 위하여 선분 사이 허용되는 최소 간격)
(이 값이 크면 끊어진 선분을 하나로 잇는 데 용이하나, 너무 크면 관련없는 선분이 
연결될 수 있으므로 주의)
"""

# 확률적 허프 변환으로 찾은 직선 그리기
if lines_probabilistic is not None:
    for line in lines_probabilistic:
        x1, y1, x2, y2 = line[0]
        cv2.line(image, (x1, y1), (x2, y2), (0, 255, 0), 2)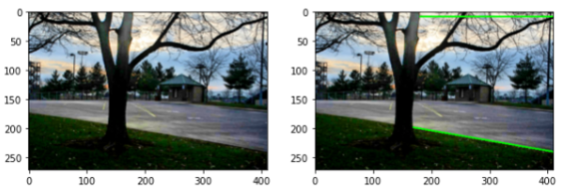

여기서 설정된 임계값은, 테스트 이미지에 맞게 적당히 올리고 내려가면서 수동으로 맞춰 주었다.

• 결과 비교