240120_최소 신장 트리(크루스칼 알고리즘)

참조: https://techblog-history-younghunjo1.tistory.com/262

최소 신장 트리

먼저 서로소 집합 자료구조를 알고오면 좋다.

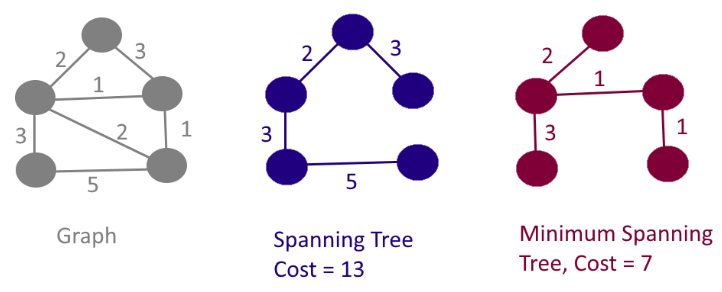
• 신장 트리란, 하나의 그래프가 있을 때 모든 노드를 포함하면서, 즉 모든 노드들 간에 서로 연결은 되어있되 사이클이 존재하지 않는 부분 그래프를 의미한다.
• 즉 최소 신장 트리란, 사이클이 없이 모든 정점이 연결되어 있는 그래프이다.
• 최소 신장 트리 알고리즘에는 크루스칼, 프림 알고리즘이 있는데 여기서는 크루스칼 알고리즘을 소개한다.

크루스칼 알고리즘

동작 과정

1. 주어진 모든 간선 정보에 대해 간선 비용이 낮은 순서(오름차순)로 정렬을 수행
2. 정렬된 간선 정보를 하나씩 확인하면서 현재의 간선이 노드들 간의 사이클을 발생시키는지 확인
3. 만약 사이클이 발생하지 않은 경우, 최소 신장 트리에 포함시키고 사이클이 발생한 경우, 최소 신장 트리에 포함시키지 않음
4. 1~3번 과정을 모든 간선 정보에 대해 반복 수행

자세한 동작 과정은 해당 자료에서 참조 가능하다.

코드

import sys
input = sys.stdin.readline

v, e = map(int,input().split())
parent = [None] * (v+1)

for i in range(1, v+1):
    parent[i] = i
    
def FindParent(target):
    if parent[target] != target:
        parent[target] = FindParent(parent[target])
    return parent[target]

def Union(v1, v2):
    v1 = FindParent(v1)
    v2 = FindParent(v2)
    if parent[v1] != parent[v2]:
        if v1 > v2:
            parent[v1] = v2
        else:
            parent[v2] = v1
        
edges = []
totalCost = 0

for _ in range(e):
    v1, v2, cost = map(int, input().split())
    edges.append((cost, v1, v2))
    
edges.sort()

for i in range(e):
    c, a, b = edges[i]
    
    if FindParent(a) != FindParent(b):
        Union(a, b)
        totalCost += c
        
print(totalCost)