참조: https://www.youtube.com/watch?v=2MdsebfJOyM
참조: https://www.youtube.com/watch?v=6drLl777k-E
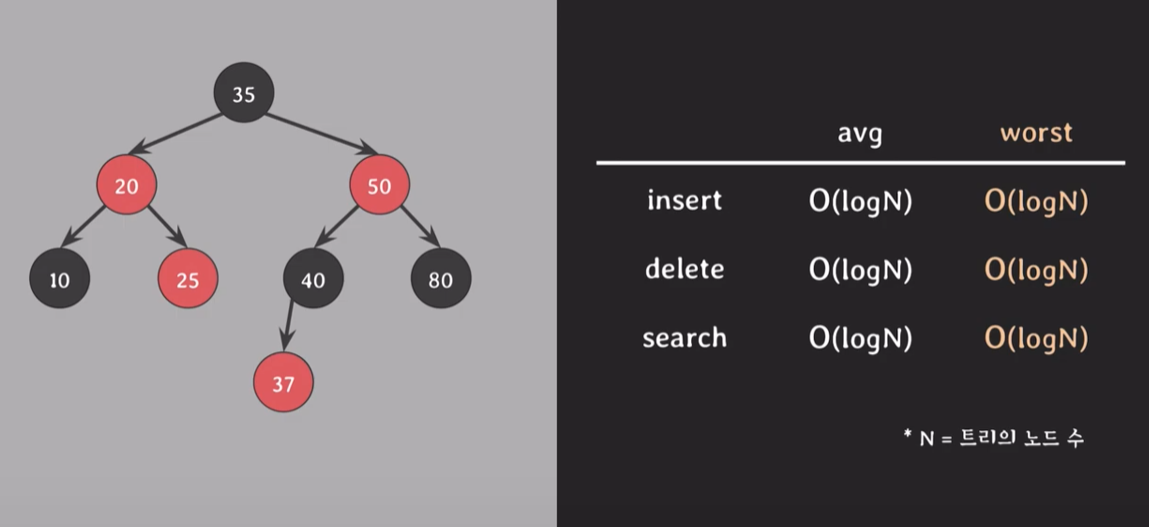
Red-Black Tree란
- 이진 트리의 한 종류로 스스로 균형을 잡는 트리(Self-balanced Binary Tree)이다.
- 이진 탐색 트리의 최악의 경우를 개선한 트리이다.
- Red-Black Tree에서 모든 노드는 검은색 아니면 빨간색으로 표시한다.
Red-Black Tree 속성
그 전에 nil노드부터 알아야한다.
존재하지 않음을 의미하는 노드이다.
값이 있는 노드와 동등한 취급을 받는 노드이며, black의 색을 가진다.
Red-Black Tree에서 자녀가 없을 때 자녀를 nil노드로 표기한다.
따라서 Red-Black Tree에서 leaf 노드는 nil노드이다.
- 모든 노드는 검은색 또는 빨간색이다.
- 루트 노드는 항상 black이다.
- 모든 nil(leaf)노드는 black이다.
- red의 재녀들은 black이다.(즉, red가 연속적으로 존재할 수 없다.)
- 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black수는 같다.(단, 자기 자신은 카운트에서 제외한다.)
Red-Black Tree는 위 다섯가지의 속성을 만족해야한다. 만약 삽입 또는 삭제로 위의 속성을 위반한다면, 만족할 때까지 재조정을 한다.
Red-Black Tree 삽입
1. 삽입은 일반적인 이진 트리와 동일하다.
2. 삽입 후에도 #5번 속성을 만족하기 위해 삽입하는 노드는 항상 red의 색을 가진다.
3. 삽입 후 RB 트리 위반 여부를 확인한다.
4. 5가지 속성 중 하나라도 위반하였다면 재조정하여 속성을 만족시킨다.
삽입 시 속성을 위반하는 경우는 다음과 같다.
1. red 삽입 후 #2 속성을 위반한 경우

루트 노드를 black으로 변경한다.
2. red삽입 후 #4 속성을 위반한 경우
Case 3
삽입된 red 노드가 부모의 왼쪽(또는 오른쪽)자녀이고
부모도 red노드이며 할아버지의 왼쪽(또는 오른쪽) 자녀이고
부모의 형제가 black노드인 상황
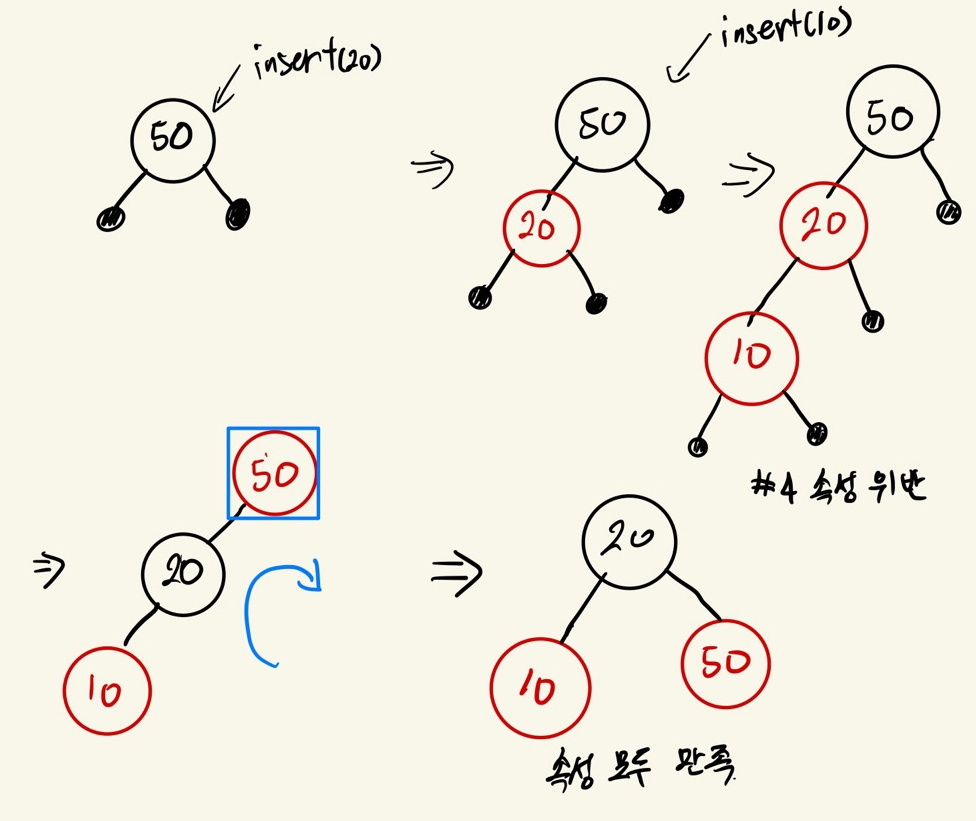
부모와 할아버지의 색을 바꾼 후 할아버지 기준으로 오른쪽(또는 왼쪽)으로 회전한다.
Case 2
삽입된 red노드가 부모의 오른쪽(또는 왼쪽) 자녀이고
부모도 red노드이고 할아버지의 왼쪽(또는 오른쪽) 자녀이고
부모의 형제가 black노드인 상황
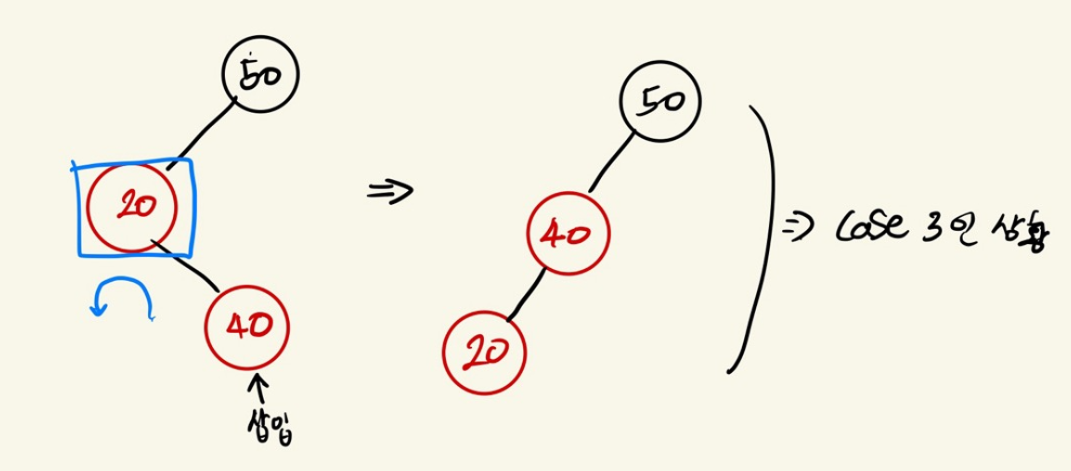
부모를 기준으로 왼쪽(또는 오른쪽)으로 회전한뒤 Case 3를 적용하여 해결
Case 1
삽인된 red노드의 부모도 red노드이고
부모의 형제도 red노드인 상황
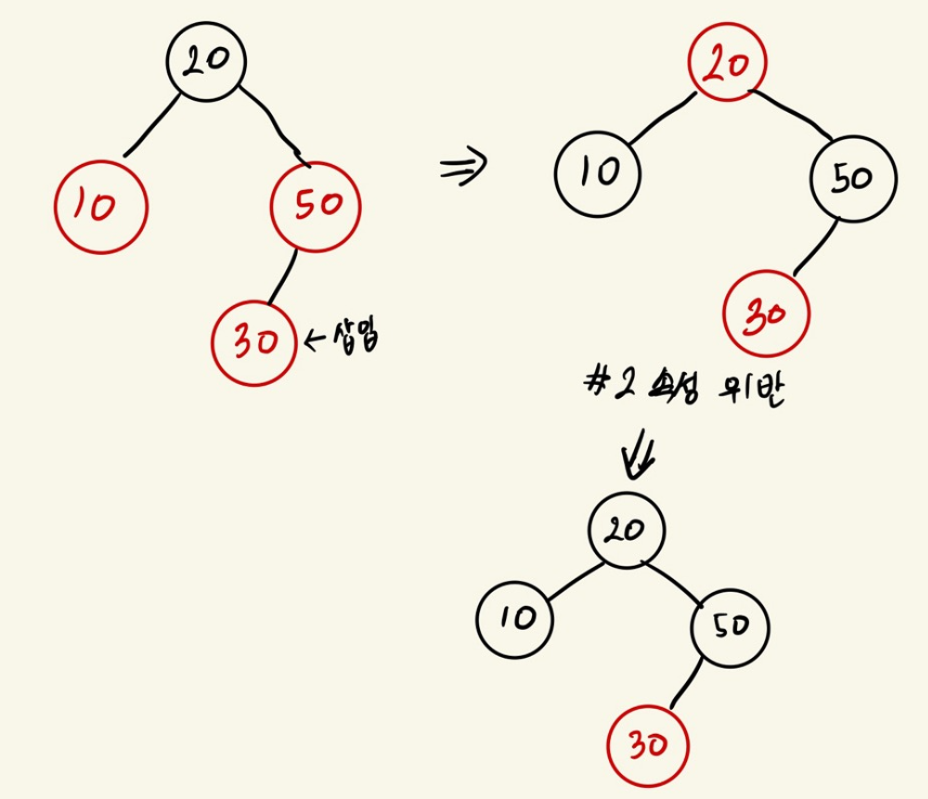
부모와 형제를 black으로 바꾸고 할아버지를 red로 바꿔준 뒤 할아버지부터 다시 확인 시작한다.
Red-Black Tree 삭제
-
삭제 시에 어떤 노드의 색이 삭제되는 가가 매우 중요하다.
- 삭제하려는 노드의 자녀가 없거나 하나인 경우: 삭제되는 색 = 삭제되는 노드의 색
- 삭제하려는 노드의 자녀가 둘인 경우: 삭제되는 색 = 삭제되는 successor의 색
-
삭제되는 색이 red일 때, 어던 속성도 위반하지 않는다.
-
삭제되는 색이 black일 때, 특수한 상황을 제외하면 #5의 속성을 위반하게 된다.
-
그래서 #5의 속성을 다시 만족시키기 위해 삭제된 색의 위치를 대체한 노드에 extra black을 부여한다.'
- extra black이란
- 경로에서 black의 수를 카운트할 때 하나의 black으로 카운트된다.
- 만약 black노드에 extra black이 부여됐다면 doubly black노드라 한다.
- 만약 red노드에 extra black이 부여됐다면 red and black노드라 한다.
삭제 시 속성을 위반하는 경우는 다음과 같다.
1. red and black 일 때
: red and black 노드를 black 노드로 바꾸어서 해결한다.
2. doubly black일 때,
Case 4
doubly black의 오른쪽(또는 왼쪽) 형제가 black노드이고
그 형제의 오른쪽(또는 왼쪽) 자녀가 red노드인 상황
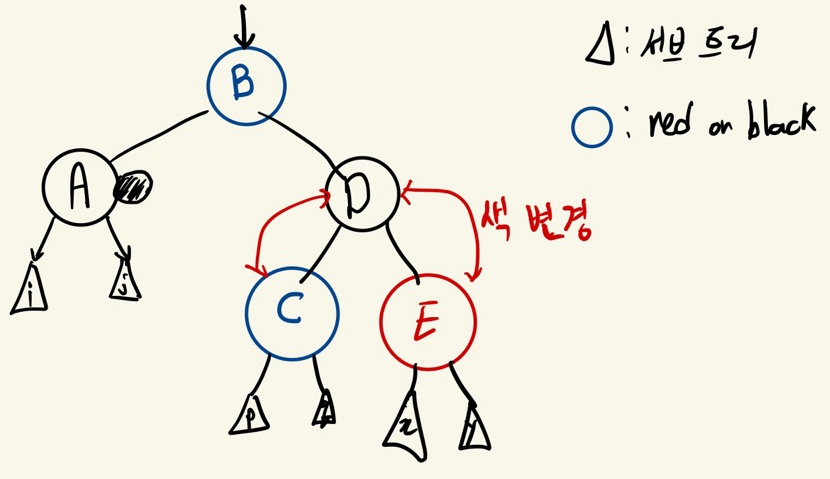
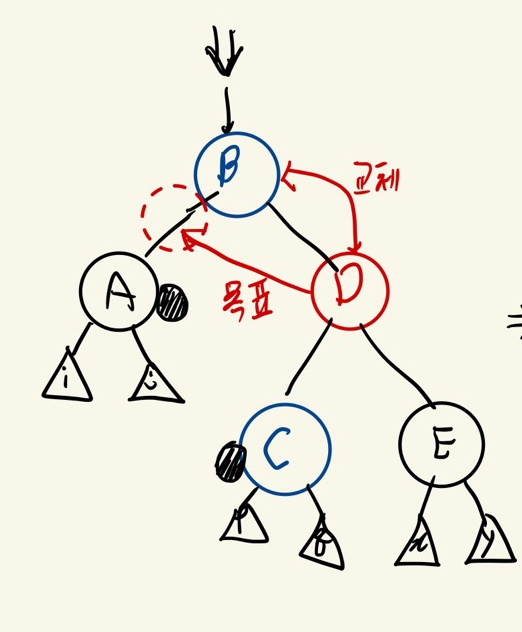
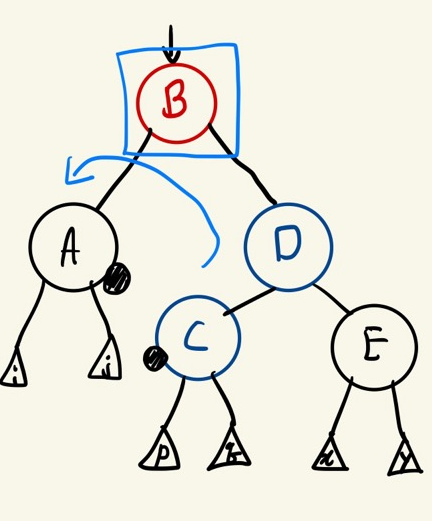
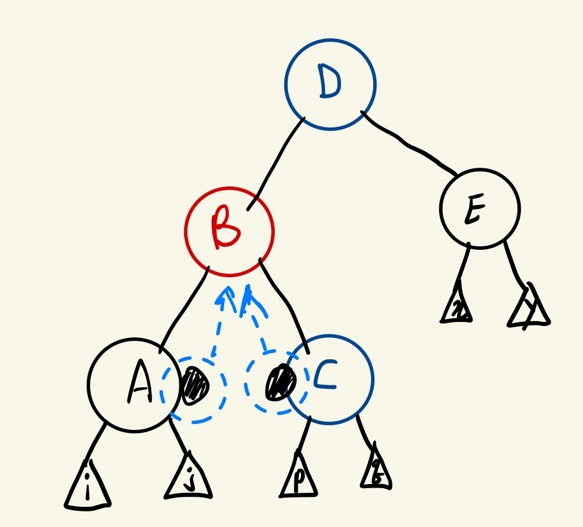
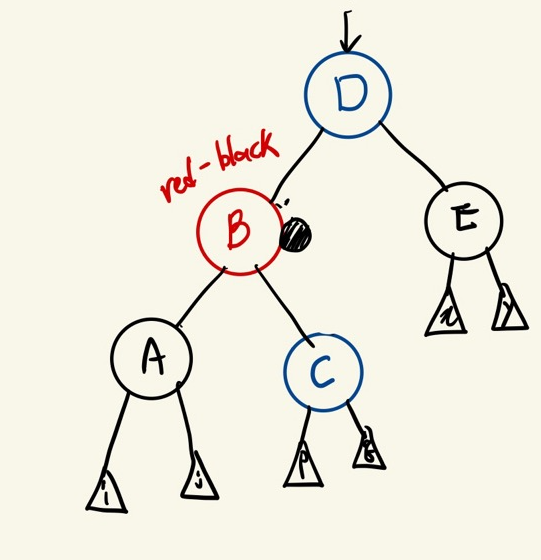
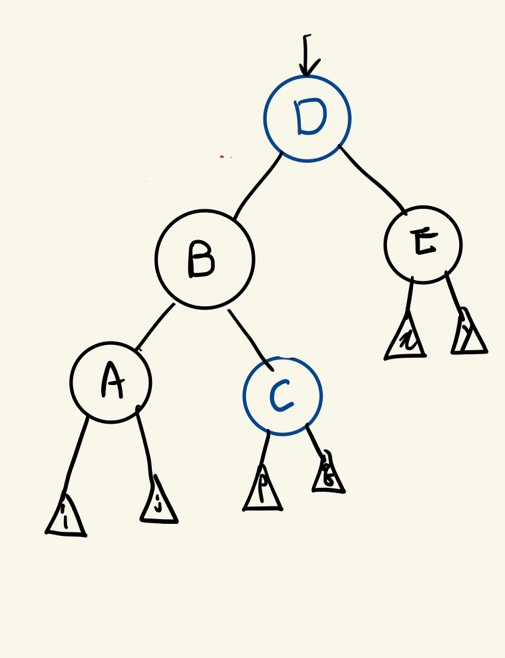
오른쪽(또는 왼쪽) 형제는 부모의 색으로 바꾸고, 오른쪽(또는 왼쪽)형제의 오른쪽(또는 왼쪽) 자녀는 black으로 부모는 black으로 바꾼 후에 부모를 기준으로 왼쪽(또는 오른쪽)으로 회전한다.
Case 3
doubly black의 오른쪽(또는 왼쪽)형제의 자녀가 red노드이고
그 형제의 오른쪽(또는 왼쪽) 자녀가 black노드인 상황
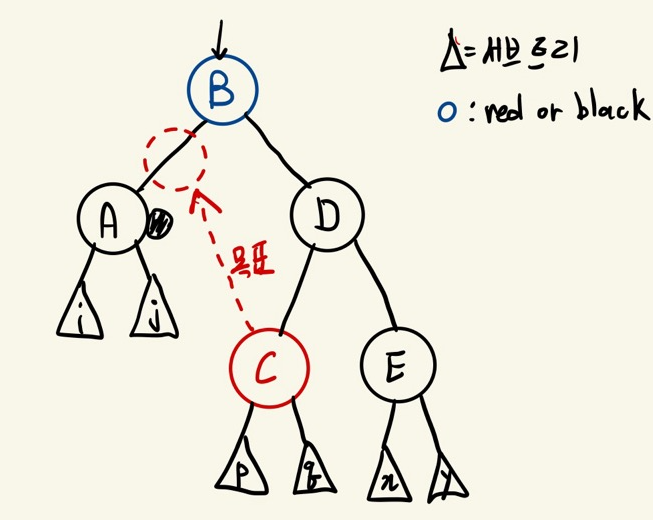
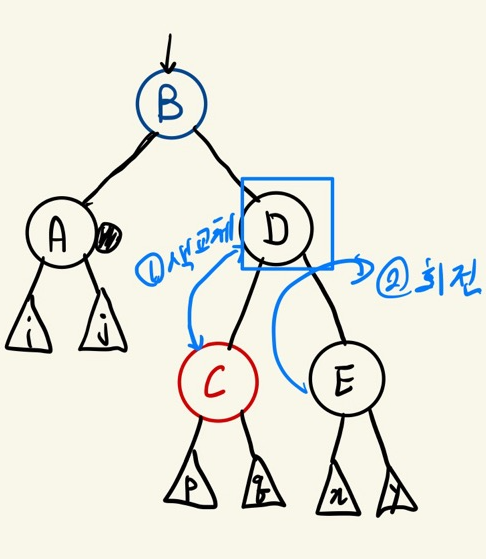
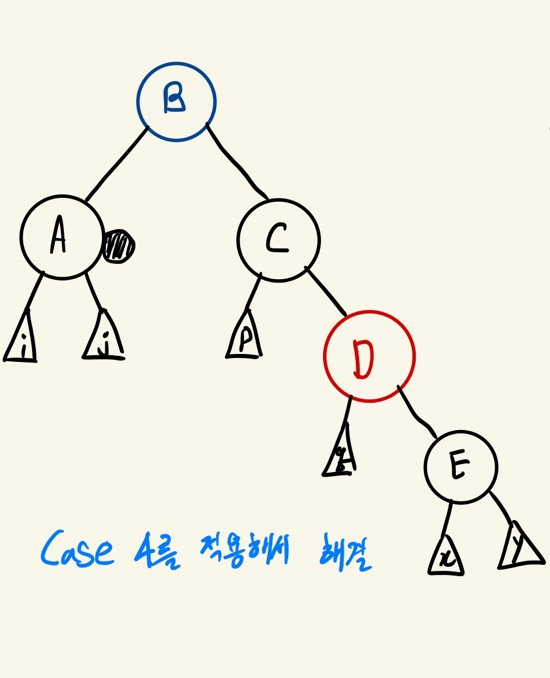
doubly black노드 형제의 오른쪽(또는 왼쪽) 자녀를 red노드가 되게 만들고 이후 case 4를 적용하여 해결
Case 2
doubly black의 형제가 black노드이고
그 형제의 두 자녀 모두 black인 상황
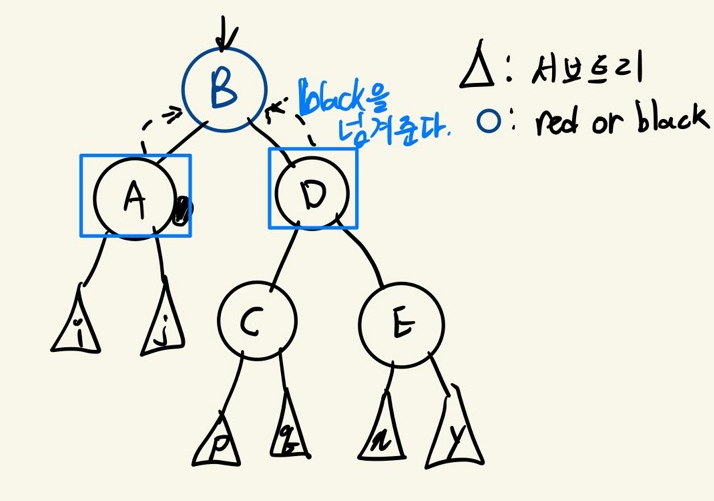
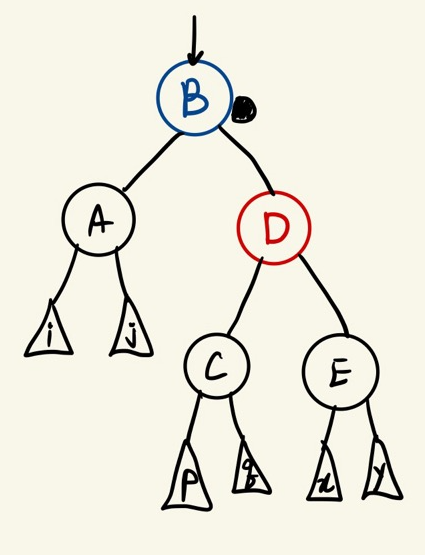
doubly black과 그 형제의 black을 모아서 부모에게 전달해주고 부모가 해결하도록 위임한다.
Case 1
doubly black의 오른쪽(또는 왼쪽) 형제가 red노드인 상황
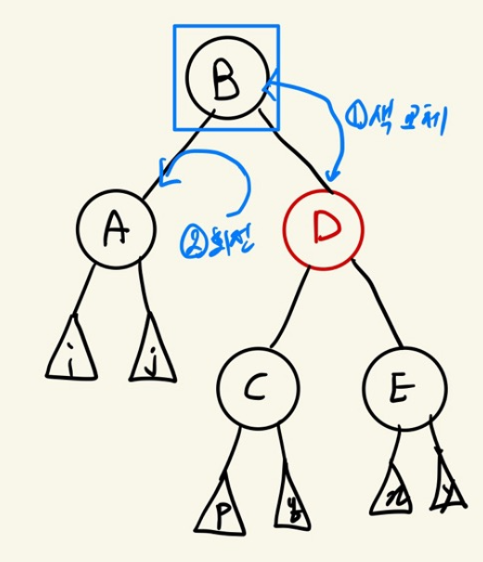
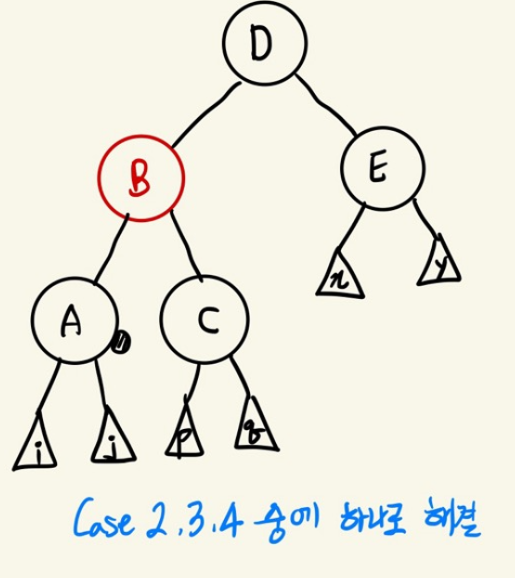
부모와 형제의 색을 바꾸고 부모를 기준으로 왼쪽(또는 오른쪽)으로 회전한 뒤 doubly black을 기준으로 Case 2,3,4 중에 하나로 해결
Red-Black Tree의 시간 복잡도