[11726] 2×n 타일링

💁‍♀️ DP 사용

DP를 사용한다지만 처음에 규칙발견하기가 조금 힘들었다.

가로의 길이만 변해서 그 안에서 규칙을 발견하려했는데, 처음에는 1,2,3을 조합해서 가로길이가 되는 경우의수를 구한 후 1,2,3에 해당하는 값을 가지고 어떻게하려고접근했었다.

예를들어 가로가 5라면 122, 221 의 조합을 생각해볼 수 있고,,, 그런데 이렇게하면 여러 경우의수들이 겹친다.

접근 방법

1부터 N-1크기의 직사각형과 관련된 경우의 수를 모두 구해놓았다고 가정하고 문제에 접근해보자.

D[N] : 길이 N으로 만들 수 있는 타일의 경우의 수

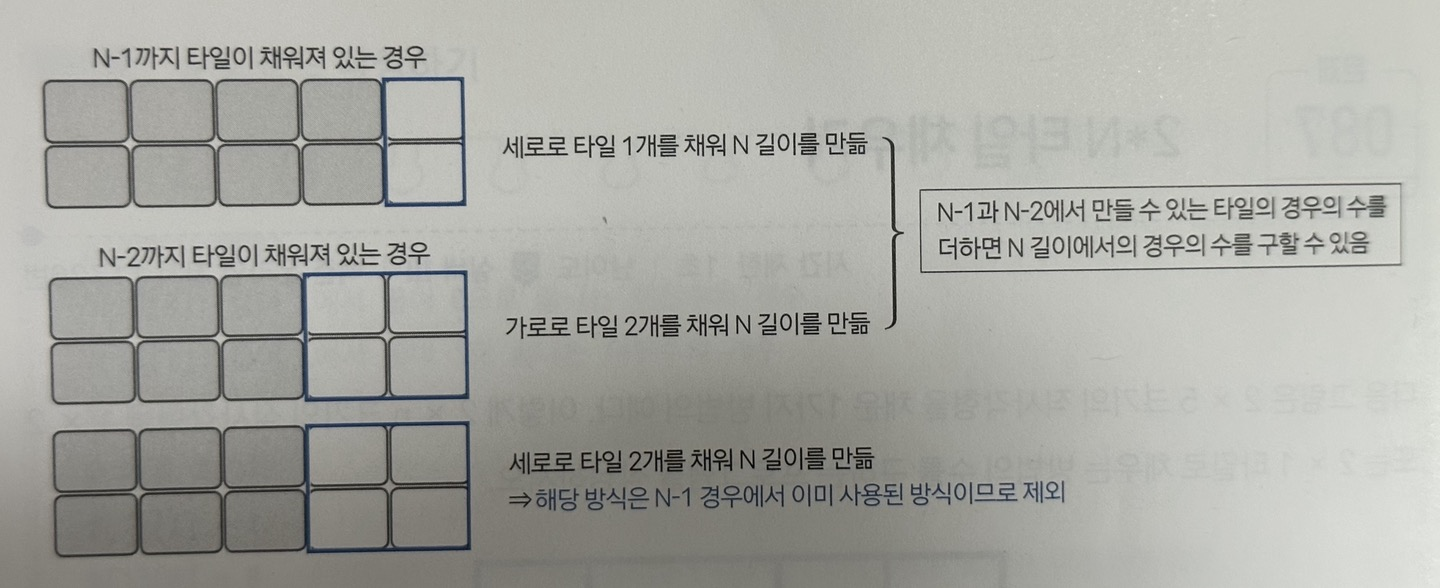
이렇게 N-1, N-2까지만 겹치지않는 경우의수를 체크할 수 있다.
(N-3은 결곡 N-1, N-2에서 N을 만들기 위해 고려할 수 있는 경우의수와 겹침)
이 부분을 이해하는데 조금 생각이 필요했다.
정말 빼먹은경우의수가 하나도 없을것인지. 이건 몇가지 경우의수를 그려보면 이해된다.

점화식

D[N] = D[N-1] + D[N-2]

Troubleshooting

import java.io.*;
import java.util.*;

class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(br.readLine());
		int[] answer = new int[n+1];
		if(n == 1) {
			System.out.println("1");
			return;
		}
		if(n == 2) {
			System.out.println("2");
			return;
		}
		answer[1] = 1;
		answer[2] = 2;
		
		for(int i=3;i<=n; i++) {
			answer[i] = answer[i-1] + answer[i-2]; // trouble
		}
		System.out.println(answer[n]%10007); 
	}
}

문제

틀렸습니다

원인

혹시 값 범위를 넘어가는게 문제인가?

해결

answer타입을 int에서 long으로 수정했다.

Troubleshooting

문제

여전히 틀렸습니다.

원인

간단한 코드기에 로직상 틀린부분이 너무 안보였다. 모범답안을 참고했다.
모범답안은 나머지연산을 answer[i]에 값을 넣기전에 수행한 후 값을 넣어주는것을 발견했다.

문제를 읽으면 출력전 출력할 데이터만 10007로 나눈 나머지로 출력하면되는거아닌가? 모든 값을 꼭 나머지연산해서 넣어야하나 싶었다..

나머지연산하기 전 덧셈만 한 것을 확인해보니 long타입의 범위도 넘어간다..! overflow가 발생해서 계속 수가 도는것을 확인할 수 있었다.

해결

answer[i] = (answer[i-1] + answer[i-2]) %10007;로 나머지연산을 진행한 후 값을 대입했다.

제출 코드

import java.io.*;
import java.util.*;

class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(br.readLine());
		int[] answer = new int[n+1];
		if(n == 1) {
			System.out.println("1");
			return;
		}
		if(n == 2) {
			System.out.println("2");
			return;
		}
		answer[1] = 1;
		answer[2] = 2;
		
		for(int i=3;i<=n; i++) {
			answer[i] = (answer[i-1] + answer[i-2]) %10007;
		}
		System.out.println(answer[n]);
	}
}

공부한 사항

• mod 연산을 한 결과값을 출력해야 할 때에는 반드시 연산할 때마다 mod 연산을 해주어야 한다. 계속 숫자를 더하고 마지막 출력시에만 mod연산을 해줄 경우 범위를 넘어 Overflow가 발생하기 때문에 잘못된 값이 출력될 수 있다.

• 나머지 연산에대해 (a+b)%c = a%c + b%c가 성립하는줄 알았는데, 아니었다.

(A + B) % p = ((A % p) + (B % p)) % p
(A * B) % p = ((A % p) * (B % p)) % p
(A - B) % p = ((A % p) - (B % p) + p) % p