[백준] 11004 : K번째 수 - JAVA

🙋 퀵 정렬 이용!

문제분석

제한시간은 2초인데, N의 최대는 5,000,000이다.
퀵정렬은 O(NlogN)의 시간복잡도를 가지는데 계산하면 100,000,000. 즉 1억이므로 2초 시간내에 가능하다고 판단된다.
pivot을 어떤값으로 설정하는지가 관건!!!
-> 데이터가 대부분 정렬되어있는 경우 앞쪽에 있는 수를 pivot으로 선택하면 불필요한 연산이 많아진다. 따라서 중간 위치를 pivot으로 설정하는게 좋다.

<pivot 정하는 법>
pivot == K : K번째 수를 찾은 것이므로 알고리즘 종료
pivot > K : pivot의 왼쪽 부분에 K가 있으므로 왼쪽(S~pivot-1)만 정렬 수행
pivot < K : pivot의 오른쪽 부분에 K가 있으므로 오른쪽(pivot+1 ~ E)만 정렬 수행

슈도코드

N,K 입력받기
for(N번 만큼 반복) {
	배열에 입력받은 원소 삽입   
}
quickSort()
A[k]출력 

quickSort() {
	pivot = 가장 처음값으로 설정
    start = pivot 인덱스 +1
    end = 가장 오른쪽 값
    if(start 인덱스 >= end인덱스) {
    	end 값 pivot값 교환
    	break;
    }
    if(start 값 > pivot 값 && end 값 < pivot 값) {
    	두 값 바꾸기
        end--
        start++
        quickSort()
    }
    if(end 값 < pivot 값 && start값 <= pivot값) {
        start++
        quickSort()
    }
    if(start 값 > pivot값 && end값 >= pivot값) {
    	end--
    	quickSort()
    }
}

---

Troubleshooting

import java.util.Scanner;

public class Main {
static int[] A;
static int N;
static int pivot = 0;
static int start = pivot +1;
static int end;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		end = N-1;
		A = new int[N];
		int K = sc.nextInt();
		sc.nextLine();
		for(int i=0; i<N; i++) {
			A[i] = sc.nextInt();   
		}
		quickSort(A);
		System.out.println(A[K]);
	}
	public static void quickSort(int[] A) {
	    if(start +1 == end) return;
	    if(start >= end) {
	    	return;
	    }
	    if(A[start]> A[pivot] && A[end] < A[pivot]) {
	    	swap(A[start], A[end]);
	        end--;
	        start++;
	        quickSort(A);
	    }
	    if(A[end] < A[pivot]&& A[start] <= A[pivot]) {
	        start++;
	        quickSort(A);
	    }
	    if(A[start]> A[pivot] && A[end] >= A[pivot]) {
	    	end--;
	    	quickSort(A);
	    }
	    pivot++;
	}
	
	public static void swap(int start, int end) {
		int temp = end;
		end = start;
		start = temp;
	}

}

문제

백준에서 틀렸다는 결과를 받았다.

원인

디버깅을 해보니, 예제에서 처음에 pivot = 4, start = 1 , end = 5 일때 start, end의 값은 그 위치가 맞으므로 각각 인덱스만 바뀌어야한다.
하지만 이렇게 둘 다 제자리일때 해당하는 조건문이 없다! 따라서 재귀호출이 안된다.

해결

둘 다 제자리일때 조건문을 추가했다.

if(A[start] <= A[pivot] && A[end] >= A[pivot]) {
	    	start++;
	    	end--;
	    	quickSort(A);
	    }

Troubleshooting 2

import java.util.Scanner;

public class Main{
static int[] A;
static int N;
static int pivot = 0;
static int start = pivot +1;
static int end;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		end = N-1;
		A = new int[N];
		int K = sc.nextInt();
		sc.nextLine();
		for(int i=0; i<N; i++) {
			A[i] = sc.nextInt();   
		}
		quickSort(A);
		System.out.println(A[K]);
	}
	public static void quickSort(int[] A) {
	    if(start +1 >= end) return;
	    if(start >= end) {
	    	return;
	    }
	    if(A[start]> A[pivot] && A[end] < A[pivot]) {
	    	swap(A[start], A[end]);
	        end--;
	        start++;
	        quickSort(A);
	    }
	    if(A[end] < A[pivot]&& A[start] <= A[pivot]) {
	        start++;
	        quickSort(A);
	    }
	    if(A[start]> A[pivot] && A[end] >= A[pivot]) {
	    	end--;
	    	quickSort(A);
	    }
	    if(A[start] <= A[pivot] && A[end] >= A[pivot]) {
	    	start++;
	    	end--;
	    	quickSort(A);
	    }
	    pivot++;
	}
	
	public static void swap(int start, int end) {
		int temp = end;
		end = start;
		start = temp;
	}

}

문제

백준에서 시간초과가 났다.

원인

1. 앞쪽에 있는 수를 피벗으로 선택했다.

2. 모든 부분에 퀵정렬을 돌렸다.

해결

1. 앞쪽에 있는 수를 피벗으로 선택하면 불필요한 연산이 많아져서, 배열의 중간위치를 피벗으로 설정해야할것같다.

   -> 퀵정렬은 최악의 경우 O(N^2)의 시간복잡도를 가지는데, 이 부분을 간과했다!

2. 또한 K가 피벗보다 오른쪽에있는지(큰지), 왼쪽에있는지(작은지), 같은지 판단하여 알고리즘을 멈추거나 필요한부분만 정렬을 수행할 수 있도록 해야겠다.

---

제출코드

import java.util.Scanner;

public class Main {
static int N;
static int pivot;
static int index = 0;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		int[] A = new int[N];
		int K = sc.nextInt();
		sc.nextLine();
		for(int i=0; i<N; i++) {
			A[i] = sc.nextInt();   
		}
		quickSort(A, 0, N-1, K-1);
		System.out.println(A[K-1]);
	}
	public static void quickSort(int[] A,int S, int E, int K) {
		if(S < E) {
			int pivot = partition(A,S,E);
			if(pivot == K) return;
			else if(K <pivot) quickSort(A,S,pivot-1,K);
			else quickSort(A,pivot+1, E, K);
		}
	}
	
	public static int partition(int[] A, int S, int E) {
		if(S+1 == E) {
			if(A[S] > A[E]) {
				swap(A,S,E);
			}
			return E; // why??
		}
		int M = (S+E) /2;
		swap(A,S,M);
		int pivot = A[S];
		int l = S+1, r = E;
		while(l <= r) {
			while(pivot < A[r] && r>0) r--;
			while(pivot > A[l] && l<A.length-1) l++;
			if(l <= r) swap(A,l++,r--);
		}
		A[S] = A[r]; 
		A[r] = pivot;
		return r;
		
	}
	
	public static void swap(int[] A, int start, int end) {
		int temp = A[end];
		A[end] = A[start];
		A[start] = temp;
	}

}

의문

partition함수에서 처음 if문에서 returnE를 하는부분에 주석으로 'why??'를 달아두었다.
검사하는 사이즈가 2일경우, 오름차순으로 정렬하고나서 무조건 뒤의값(E)를 리턴하는건데, '왜 S가 아닌 E일까?'하는 의문이 들었다.

해결

만일 E가 K가 아닐경우, quickSort함수에서 K < pivot조건에 해당하는 코드로 들어가서 재귀호출을 하게되는데, 이 경우에는 사이즈가 1이되므로 (즉 S == E) quickSort가 수행되지 않는다.
하지만 결국 정렬은 다 된것이기에, main함수에서 A[K-1]을 출력하면 정답이 나온다.

---

핵심 로직

1. 중간 위치를 pivot으로 설정한 후, 맨 앞의 값과 swap.
   -> pivot을 맨 앞으로 옮기는 이유 : l,r 이동을 편하게 하기 위해
   -> l,r : 이후 pivot을 제외한 그룹에서 왼쪽, 오른쪽 끝으로 정한다.

2. 우선 r을 이동한다. r의 값이 pivot의 값보다 크면 r-- 연산 반복
   r을 이동한 후, l가 pivot보다 작으면서 l보다 r이 크면 l++연산 반복
   -> 만약, l,r의 위치가 같다면 l 이동x)

3. pivot을 두 집합으로 나눠주는 위치, 즉 l,r이 만난 위치와 swap

---

헷갈렸던 부분

1. if(l <= r) swap(A,l++,r--);의 뜻
   l,r의 값이 바뀐 후, l은 1증가, r은 1감소한다!

A[S] = A[r]; 
A[r] = pivot;
return r;

에서 A[S] = A[l];이 아닌, A[S] = A[r];인 이유가 궁금했다.
어떤 상황에서든 r이랑 교환해주는게 맞나?

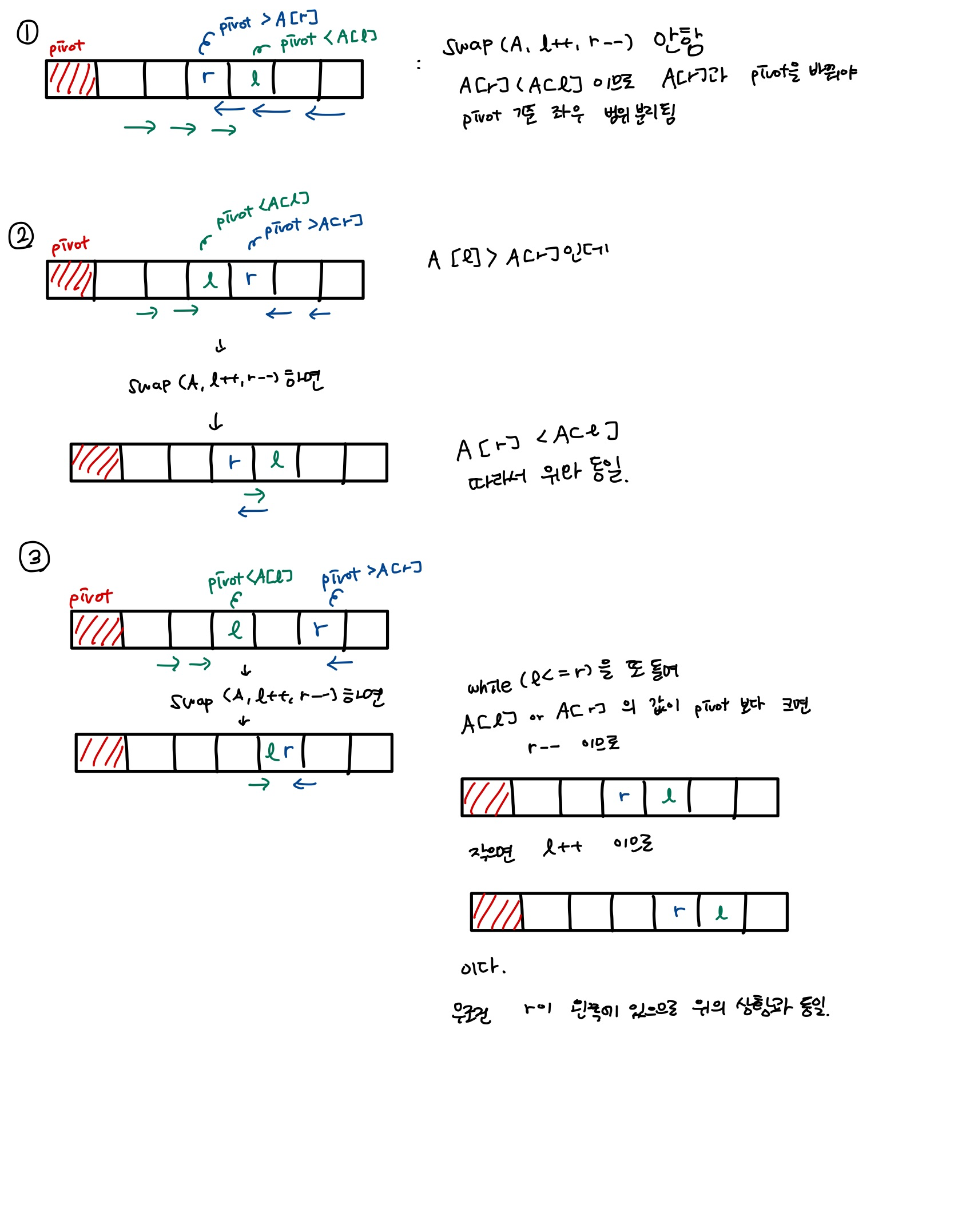
분석결과 이해완료!