🙋🏻♀️ 벨만-포드 사용!
Troubleshooting 1
import java.util.ArrayList;
import java.util.Arrays;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.BufferedWriter;
import java.io.OutputStreamWriter;
import java.io.IOException;
import java.util.StringTokenizer;
import java.util.Queue;
import java.util.LinkedList;
public class Main {
public static long[] distance;
public static int N,M,W;
public static ArrayList<node> road;
public static Queue<Integer> q = new LinkedList<>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int TC = Integer.parseInt(br.readLine());
StringTokenizer st;
for(int i=0; i<TC; i++) {
road = new ArrayList<>();
boolean isPossible = false;
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
W = Integer.parseInt(st.nextToken());
distance = new long[N+1];
for(int j=0; j<M; j++) {
st = new StringTokenizer(br.readLine());
int S = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
int T = Integer.parseInt(st.nextToken());
road.add(new node(S,E,T));
road.add(new node(E,S,T));
}
for(int k=0; k<W; k++) {
st = new StringTokenizer(br.readLine());
int S = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
int T = Integer.parseInt(st.nextToken())*(-1);
road.add(new node(S,E,T));
}
for(int p=1; p<N+1; p++) {
Arrays.fill(distance, Long.MAX_VALUE);
distance[p] = 0;
bellmanFord(p);
if(distance[p] < 0) {
isPossible = true;
break;
}
}
if(isPossible)System.out.println("YES");
else System.out.println("NO");
}
}
public static void bellmanFord(int v) {
for(int i=1; i<=N; i++) {
for(int k=0; k<road.size(); k++) {
int from = road.get(k).start;
int to = road.get(k).end;
int time = road.get(k).time;
if(distance[from] == Long.MAX_VALUE) continue;
if(distance[to] > distance[from] + time) {
distance[to] = distance[from] + time;
if(i > N-1) distance[to] = Long.MIN_VALUE;
}
}
}
}
}
class node {
int start,end,time;
public node(int start, int end, int time) {
this.start = start;
this.end = end;
this.time = time;
}
}문제
91%까지 가다가 시간초과가났다.
원인
아무래도 모든 노드를 한번씩 다 벨만포드알고리즘을 수행하는게 문제인것같다.
(distance[i] <0이면 break;하긴 하지만 최악의 경우도 있으니,, )
해결
벨만포드를 수행하고, 모든 노드를 차례로 검사하면서 각 차례의 distance값이 음수일때 반복문을 끝내는게아니라, 어떤 노드차례여도 그 그래프에 음수 사이클이 있다면 해당 노드의 distance값이 음수인지아닌지 상관없이 끝내도록 수정했다.
if(distance[p] < 0) {
isPossible = true;
break;
}위 코드에서 아래 코드로 수정
if(isInfinite) {
isPossible = true;
break;
}추가로 필요한 부분 수정
Troubleshooting 2
import java.util.ArrayList;
import java.util.Arrays;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.BufferedWriter;
import java.io.OutputStreamWriter;
import java.io.IOException;
import java.util.StringTokenizer;
import java.util.Queue;
import java.util.LinkedList;
public class Main {
public static long[] distance;
public static int N,M,W;
public static ArrayList<node> road;
public static Queue<Integer> q = new LinkedList<>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int TC = Integer.parseInt(br.readLine());
StringTokenizer st;
for(int i=0; i<TC; i++) {
boolean isPossible = false;
road = new ArrayList<>();
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
W = Integer.parseInt(st.nextToken());
distance = new long[N+1];
for(int j=0; j<M; j++) {
st = new StringTokenizer(br.readLine());
int S = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
int T = Integer.parseInt(st.nextToken());
road.add(new node(S,E,T));
road.add(new node(E,S,T));
}
for(int k=0; k<W; k++) {
st = new StringTokenizer(br.readLine());
int S = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
int T = Integer.parseInt(st.nextToken())*(-1);
road.add(new node(S,E,T));
}
for(int p=1; p<N+1; p++) {
Arrays.fill(distance, Long.MAX_VALUE);
distance[p] = 0;
boolean isInfinite = bellmanFord(p);
if(isInfinite) {
isPossible = true;
break;
}
}
if(isPossible)System.out.println("YES");
else System.out.println("NO");
}
}
public static boolean bellmanFord(int v) {
boolean isInfinite = false;
for(int i=1; i<=N; i++) {
for(int k=0; k<road.size(); k++) {
int from = road.get(k).start;
int to = road.get(k).end;
int time = road.get(k).time;
if(distance[from] == Long.MAX_VALUE) continue;
if(distance[to] > distance[from] + time) {
distance[to] = distance[from] + time;
if(i > N-1) isInfinite = true;
}
}
}
return isInfinite;
}
}
class node {
int start,end,time;
public node(int start, int end, int time) {
this.start = start;
this.end = end;
this.time = time;
}
}문제
여전히 시간초과가 난다.
원인
다른 해설을 참고했다.
정상적인 벨만포드 함수를 실행하는데, 모든 간선을 반복했음에도 업데이트가 되지않는다면 이후에 굳이 실행할 필요가없다. 이 부분이 시간초과의 원인이다.
해결
벨만포드함수에서 N-1번만큼은 각 횟수마다 모든 간선을 실행하는데, 이때 M번째(M은 1~(N-1)) 반복에서 한 번 모든 간선을 검사하는데에도 업데이트가 전혀 일어나지않는다면, 다음번 M+1번째 반복에서 또 모든간선만큼 실행할필요없이 그냥 벨만포드를 끝내도록 수정했다.
그렇게 쭉 반복하더라도 업데이트는 여전히 되지않을것이기때문이다.
-> 이렇게 수정한다면, Troublesooting 1에서 했듯이 distance가 음수값인지로 체크해도 잘 통과된다.
제출 코드
package DFS;
import java.util.ArrayList;
import java.util.Arrays;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.BufferedWriter;
import java.io.OutputStreamWriter;
import java.io.IOException;
import java.util.StringTokenizer;
import java.util.Queue;
import java.util.LinkedList;
public class warmHall {
public static long[] distance;
public static int N,M,W;
public static ArrayList<node> road;
public static Queue<Integer> q = new LinkedList<>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int TC = Integer.parseInt(br.readLine());
StringTokenizer st;
for(int i=0; i<TC; i++) {
boolean isPossible = false;
road = new ArrayList<>();
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
W = Integer.parseInt(st.nextToken());
distance = new long[N+1];
for(int j=0; j<M; j++) {
st = new StringTokenizer(br.readLine());
int S = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
int T = Integer.parseInt(st.nextToken());
road.add(new node(S,E,T));
road.add(new node(E,S,T));
}
for(int k=0; k<W; k++) {
st = new StringTokenizer(br.readLine());
int S = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
int T = Integer.parseInt(st.nextToken())*(-1);
road.add(new node(S,E,T));
}
for(int p=1; p<N+1; p++) {
Arrays.fill(distance, Long.MAX_VALUE);
distance[p] = 0;
boolean isInfinite = bellmanFord(p);
if(isInfinite) {
isPossible = true;
break;
}
}
if(isPossible)System.out.println("YES");
else System.out.println("NO");
}
}
public static boolean bellmanFord(int v) {
boolean isInfinite = false;
for(int i=1; i<=N; i++) {
boolean update = false;
for(int k=0; k<road.size(); k++) {
int from = road.get(k).start;
int to = road.get(k).end;
int time = road.get(k).time;
if(distance[from] == Long.MAX_VALUE) continue;
if(distance[to] > distance[from] + time) {
distance[to] = distance[from] + time;
update = true;
if(i > N-1) isInfinite = true;
}
}
if (!update) {
break;
}
}
return isInfinite;
}
}
class node {
int start,end,time;
public node(int start, int end, int time) {
this.start = start;
this.end = end;
this.time = time;
}
}다른 풀이
나는 모든 정점을 출발점으로 조사해서 음의 사이클이 발생하는지 확인했는데, 다른 풀이를 찾아보니 아무 정점을 출발점으로 조사해서 음의 사이클이 발생하는지 확인하는 방법도 있다.
하지만 이 풀이해서는 주의할 점이 있다!
위 코드나, 기본 벨만포드 알고리즘을 보면, 거리배열값을 업데이트하기전에 dist[i] != INF라는 조건이 있다.(혹은 distance[i] != Long.MIN_VALUE)
이것은 아직 방문하지 않은 단절된 곳을 의미하며, 이 곳을 시작점으로 삼아서 다른 곳으로 이동하는 것은 불가능하다.
예를 들어 아래와 같은 그래프가 있다고 가정해보자.
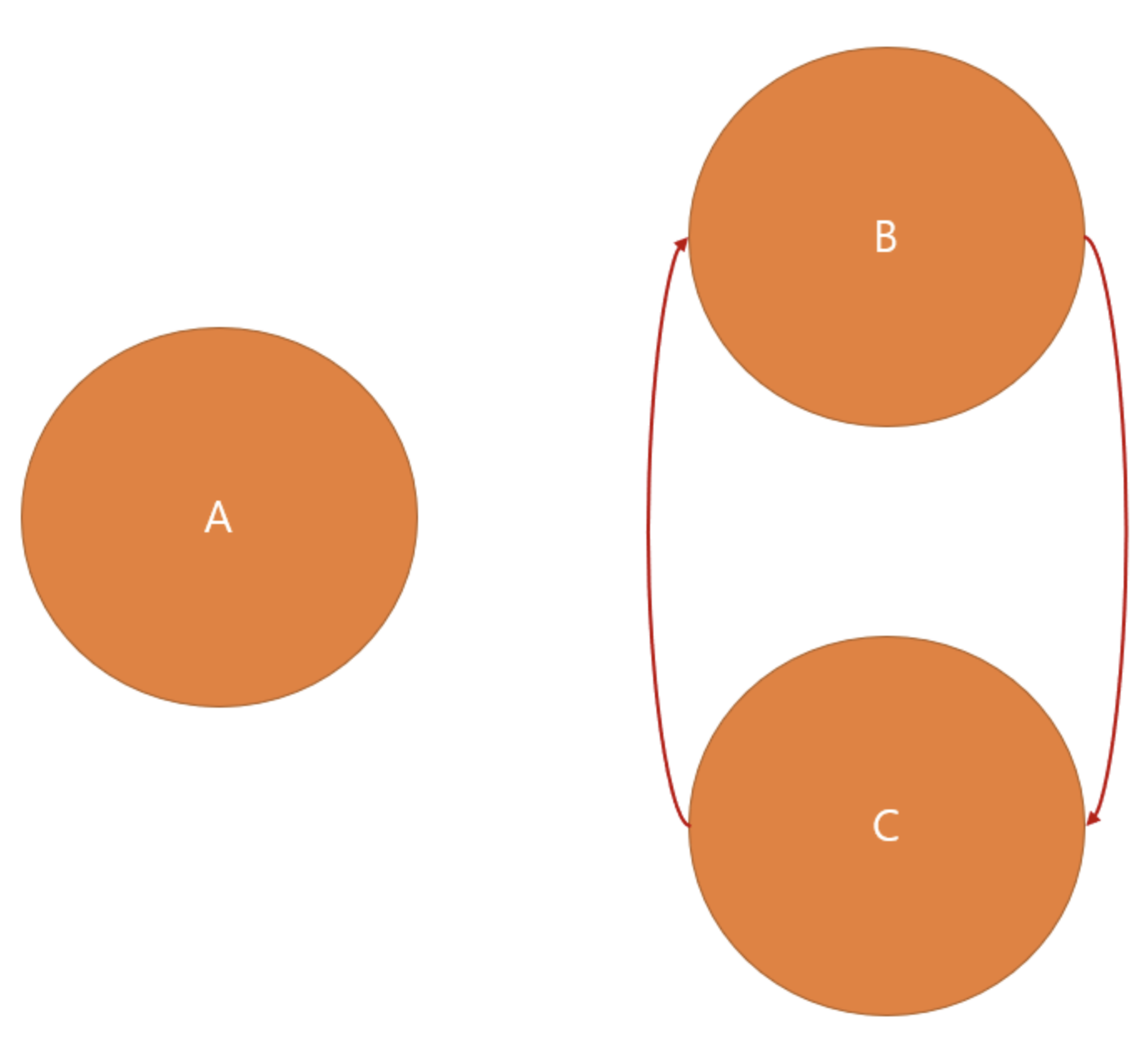
출발점이 A라고 한다면, dist[A] = 0, dist[B] = INF, dist[C] = INF일 것이다.
그리고 첫 번째 풀이 방식에서 사용한 INF 조건을 추가하면, A에서는 다른 곳으로 탐색할 수가 없다. 하지만, B와 C에서는 음의 사이클이 발생할 수도 있다.
그래서 보통 이 풀이를 선택한 사람 중 틀린사람들은 특정 노드를 시작점으로 잡아두고, distance[i] != Long.MIN_VALUE조건을 사용한 사람들이다.
이 조건을 제거해야한다.
또 하나는 꼭 Long.MIN_VALUE값처럼 가장 작은값으로 초기화 할 필요는없다. 적절한 값으로 초기화하면된다.
그 이유는 우리가 최단거리를 구하는게아닌, 음의사이클 유무만 판단하는것이기때문이다.
