그래프 탐색
하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
DFS
depth-first search = 깊이 우선 탐색
그래프 완전 탐색 기법 중 하나
그래프 시작 노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동해 다시 탐색을 수행하는 알고리즘
- 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사
- 즉, 넓게(wide) 탐색하기 전에 깊게(deep) 탐색
- 사용하는 경우: 모든 노드를 방문 하고자 하는 경우에 이 방법을 선택한다.
- 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단하다.
- 단순 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.
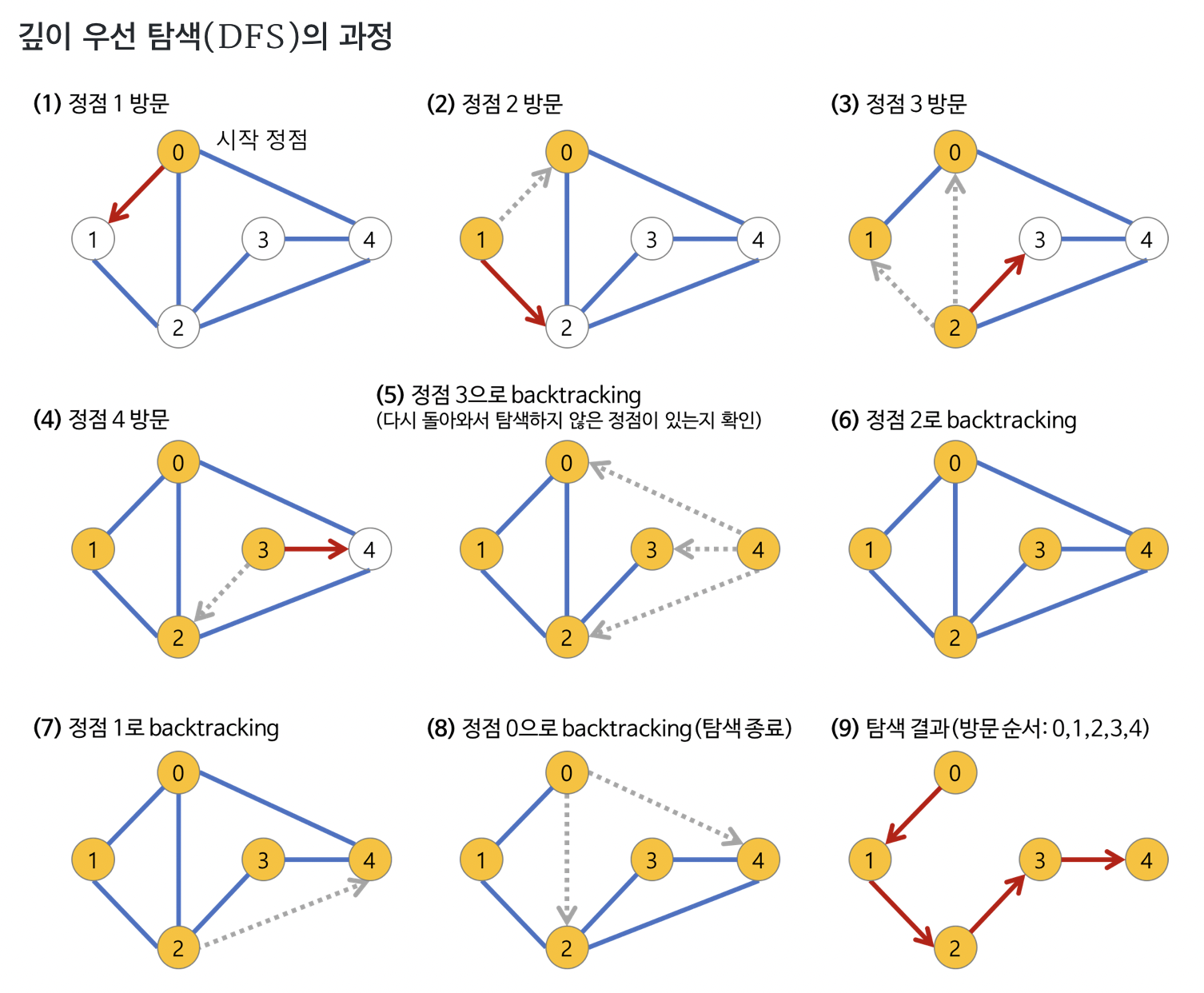
1. a 노드(시작 노드)를 방문한다.
-> 방문한 노드는 방문했다고 표시한다.
2. a와 인접한 노드들을 차례로 순회한다.
-> a와 인접한 노드가 없다면 종료한다.
3. a와 이웃한 노드 b를 방문했다면, a와 인접한 또 다른 노드를 방문하기 전에 b의 이웃 노드들을 전부 방문해야 한다.
-> b를 시작 정점으로 DFS를 다시 시작하여 b의 이웃 노드들을 방문한다.
4. b의 분기를 전부 완벽하게 탐색했다면 다시 a에 인접한 정점들 중에서 아직 방문이 안 된 정점을 찾는다.
-> 즉, b의 분기를 전부 완벽하게 탐색한 뒤에야 a의 다른 이웃 노드를 방문할 수 있다는 뜻이다.
-> 아직 방문이 안 된 정점이 없으면 종료한다.
-> 있으면 다시 그 정점을 시작 정점으로 DFS를 시작한다.
특징
- 재귀 함수로 구현 : 스택 오버플로에 유의!
- 스택 자료구조 이용
- 자기 자신을 호출하는 순환 알고리즘의 형태
- 전위 순회(Pre-Order Traversals)를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류
- 어떤 노드를 방문했었는지 여부를 반드시 검사 필수.
-> 이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.
시간 복잡도
DFS는 그래프(정점의 수: N, 간선의 수: E)의 모든 간선을 조회한다.
- 인접 리스트로 표현된 그래프: O(N+E)
- 인접 행렬로 표현된 그래프: O(N^2)
즉, 그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph) 의 경우 인접 행렬보다 인접 리스트를 사용하는 것이 유리하다.
희소 그래프
노드개수보다 간선개수가 적은 그래프
응용할 수 있는 문제
- 단절점 찾기
- 단절선 찾기
- 사이클 찾기
- 위상 정렬
핵심이론
한 번 방문한 노드를 다시 방문하면 안된다!
노드 방문 여부를 체크할 배열이 필요하며, 그래프는 인접리스트로 표현한다.
탐색방식은 후입선출의 특성을 가지므로, 이에 대한 설명은 스택을 사용해 설명한다. (구현은 재귀함수 이용)
방향이 없는 그래프는 양쪽 방향으로 에지를 모두 저장해야한다.
모든 노드를 탐색하는 데 실행한 DFS의 실행 횟수 = 연결 요소 개수
- DFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
필요한 초기작업
- 인접 리스트로 그래프 표현
- 방문 배열 초기화
- 시작 노드 스택에 삽입하기
- 스택에 삽입한 노드를 해당 위치의 방문 배열 체크(T)
- 스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입하기
- pop을 수행하여 노드를 꺼낸다
- 꺼낸 노드를 탐색 순서에 기입
- 인접 리스트의 인접 노드를 스택에 삽입하며 방문배열을 체크한다
- 스택 자료구조에 값이 없을 때까지 반복하기
- 이미 다녀간 노드는 방문배열을 바탕으로 재삽입하지 않는 것이 핵심!
사용에 적합한 문제
1) 그래프의 모든 정점을 방문하는 것이 주요한 문제
DFS, BFS 둘 다 상관없다.
2) 경로의 특징을 저장해둬야 하는 문제
예를 들면 각 정점에 숫자가 적혀있고 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용합니다. (BFS는 경로의 특징을 가지지 못합니다)
이밖에도
- 검색 대상 그래프가 정말 크다면 DFS를 고려
기본 코드
public class Dfs_cd {
static List<Integer>[] nodeList;
static int[] visited;
public static void main(String[] args) {
// 입력 데이터
int N = 5;
int[][] nodes = {{0,1},{0,2},{1,3},{1,4}};
// 리스트, 배열 초기화
nodeList = new ArrayList[N];
for(int i=0; i<N; i++) nodeList[i] = new ArrayList<>();
visited = new int[N];
// 입력받은 간선을 간선 리스트에 저장
// ex) 1-2 : nodeList[1].add(2); nodeList[2].add(1);
// 무방향성이므로 양쪽을 저장
for(int[] e : nodes){
nodeList[e[0]].add(e[1]);
nodeList[e[1]].add(e[0]);
}
visited[0] = 1; // 0부터 출발, 0은 방문 처리
dfs(0);
}
static void dfs(int cur) {
for(int next : nodeList[cur]) {
if(visited[next] == 0) { // 이어진 점이 방문한 곳이 아니면
visited[next] = 1; // 방문 처리하고
dfs(next); // 해당 점부터 재귀
}
}
}
}사이클 찾기 코드
그래프에서 사이클이 존재하는지 여부는 dfs 를 사용해서 직관적으로 찾을 수 있다.
일반적인 그래프의 코드를 살펴보도록 하자
static void dfs(int v) {
visit[v] = true;
for(int u : adj[v]) {
if(visit[u]) continue;
dfs(u);
}
}v 라는 정점을 기준으로 dfs 를 수행한다고 했을 때 dfs(v) 가 끝나기 전에 v 를 재방문하는 일이 생기면 사이클이 존재함을 알 수 있다.
아래의 코드는 dfs 를 이용한 사이클 존재 여부를 확인하는 코드이다.
static boolean cycle = false;
static boolean[] visit = new boolean[n+1];
static boolean[] finished = new boolean[n+1];
static void dfs(int v) {
visit[v] = true;
for(int u : adj[v]) {
if(!visit[u]) dfs(u);
else if(!finished[u]) cycle = true;
}
finished[v] = true;
}finished 라는 배열을 통해서 해당 정점에서의 dfs 탐색이 끝났는지 여부를 저장한다. 이 때 이미 방문한 정점의 dfs 탐색이 끝나지 않았는데 해당 정점을 재방문하는 경우 사이클이 존재함을 확인할 수 있다.
사이클 찾기 코드 2
무방향 그래프에 사이클이 존재하는지의 여부를 확인
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Stack;
import java.util.StringTokenizer;
// 무방향 그래프 -> cycle찾기
public class isCycle {
static int N, M, T, cnt, flag;
static ArrayList<Integer> adj[];
static boolean visited[];
public static void main(String[] args) throws Exception {
// TODO Auto-generated method stub
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
T = Integer.parseInt(br.readLine());
for(int test_case = 1; test_case <=T; test_case++){
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
adj = new ArrayList[N+1];
for(int i=1; i<=N; i++){
adj[i] = new ArrayList<>();
}
for(int i=1; i<=M; i++){
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
adj[u].add(v);
adj[v].add(u);
}
visited = new boolean[N+1];
if(isDfsCycle(1, -1)){
System.out.println("사이클이다");
}else{
System.out.println("사이클 아니다");
}
}
}
private static boolean isDfsCycle(int curr, int parent) {
visited[curr] = true;
for(int next : adj[curr]){
if(!visited[next]){
if(isDfsCycle(next, curr)){
return true;
}
}else if(next != parent){ //방문 했었는데, 부모노드가아니라 다른 노드일 경우니까 이건 사이클이다.
return true;
}
}
return false;
}
}출처
https://dev-typo.tistory.com/22
https://beenlife.tistory.com/54
위상정렬 코드
한 정점에서 DFS를 수행하게 되면 말단 노드까지 내려갈 것이다. 말단 노드는 진출 차수가 0이기 때문에 가장 마지막에 수행되어야 하는 작업을 뜻하게 된다.
그렇다면 LIFO 형태의 스택을 이용한다면 가장 먼저 해야 할 작업부터 가장 늦게 해야 할 작업의 순서로 출력을 쉽게 할 수 있다.
임의의 방문하지 않은 정점을 선택해도 상관이 없는 이유는 DFS는 선택한 정점보다 늦게 수행되어야 할 정점(더 깊은 정점)들만 방문하는 원리이기 때문이다.
import java.util.ArrayList;
import java.util.Stack;
class MyGraph {
int vertexCnt;
ArrayList<Integer>[] edge_List;
boolean[] visit;
boolean[] finish;
Stack<Integer> answer;
boolean cycle;
public MyGraph(int N) {
this.vertexCnt = N;
edge_List = new ArrayList[N+1];
for (int i = 0; i <= N; ++i) {
edge_List[i] = new ArrayList<>();
}
visit = new boolean[vertexCnt+1]; //방문 표시
finish = new boolean[vertexCnt+1]; //사이클 판단
answer = new Stack<>(); //결과를 담을 스택
}
public void insert_Edge(int from, int to) {
edge_List[from].add(to);
}
public void topological_Sort() {
//방문하지 않은 정점을 DFS 수행
for (int i = 1; i <= vertexCnt; ++i) {
if (cycle) {
System.out.println("그래프에 사이클 존재");
return;
}
if (!visit[i]) {
dfs(i);
}
}
//스택에 담긴 정점들을 출력
while (!answer.isEmpty()) {
System.out.print(answer.pop() + " ");
}
}
public void dfs(int v) {
visit[v] = true;
for (int i = 0; i < edge_List[v].size(); ++i) {
int nv = edge_List[v].get(i);
//방문하지 않았으면 dfs 수행
if (!visit[nv]) {
dfs(nv);
}
//방문한 정점인데 finish 체크가 되지 않았으면 사이클이 존재한다는 의미
else if (!finish[nv]) {
cycle = true;
return;
}
}
//더 이상 갈 곳이 없는 정점을 finish 체크 & 스택에 넣어줌 (말단부터 상위로)
finish[v] = true;
answer.push(v);
}
}
public class Blog {
public static void main(String[] args) {
MyGraph mg = new MyGraph(7);
mg.insert_Edge(1, 2);
mg.insert_Edge(1, 3);
mg.insert_Edge(1, 4);
mg.insert_Edge(2, 5);
mg.insert_Edge(2, 6);
mg.insert_Edge(3, 7);
mg.insert_Edge(3, 6);
mg.insert_Edge(4, 3);
mg.insert_Edge(6, 5);
mg.topological_Sort();
}
}