그리디 알고리즘
- 동적 프로그래밍 사용 시 지나치게 많은 일을 한다는 것에서 착안하여 고안된 알고리즘
- 동적 프로그래밍을 대체하는 것은 아니고 같이 쓰이며 서로 보완하는 개념
- 현재 상태에서 보는 선택지 중 최선의 선택지가 전체 선택지 중 최선의 선택지라고 가정하는 알고리즘
일반적인 그리디 알고리즘은 문제를 풀기 위한 최소한의 아이디어를 떠올릴 수 있는 능력을 요구합니다.
그리디 해법은 그 정당성 분석이 중요합니다.
- 단순히 가장 좋아보이는 것을 반복적으로 선택해도 최적의 해를 구할 수 있는지 검토합니다.
핵심이론
- 해 선택 : 현재 상태에서 가장 최선이라고 생각되는 해 선택
- 적절성 검사 : 현재 선택한 해가 전체 문제의 제약 조건에 벗어나지 않는지 검사
- 해 검사 : 현재까지 선택한 해 집합이 전체 문제를 해결할 수 있는지 검사. 전체 문제를 해결하지 못한다면 과정1로 돌아가 같은 과정 반복
특징
- 동적 계획법보다 구현하기 쉽고, 시간복잡도가 우수하다.
- 항상 최적의 해를 보장하지는 못한다.
: 그리디 알고리즘을 사용하기 전에는, 항상 적용할 때의 논리 유무를 충분히 살펴야한다.
예제
루트 노드부터 시작하여 거쳐가는 노드 값의 합을 최대로 만들고 싶습니다.
Q. 최적의 해는 무엇인가요?
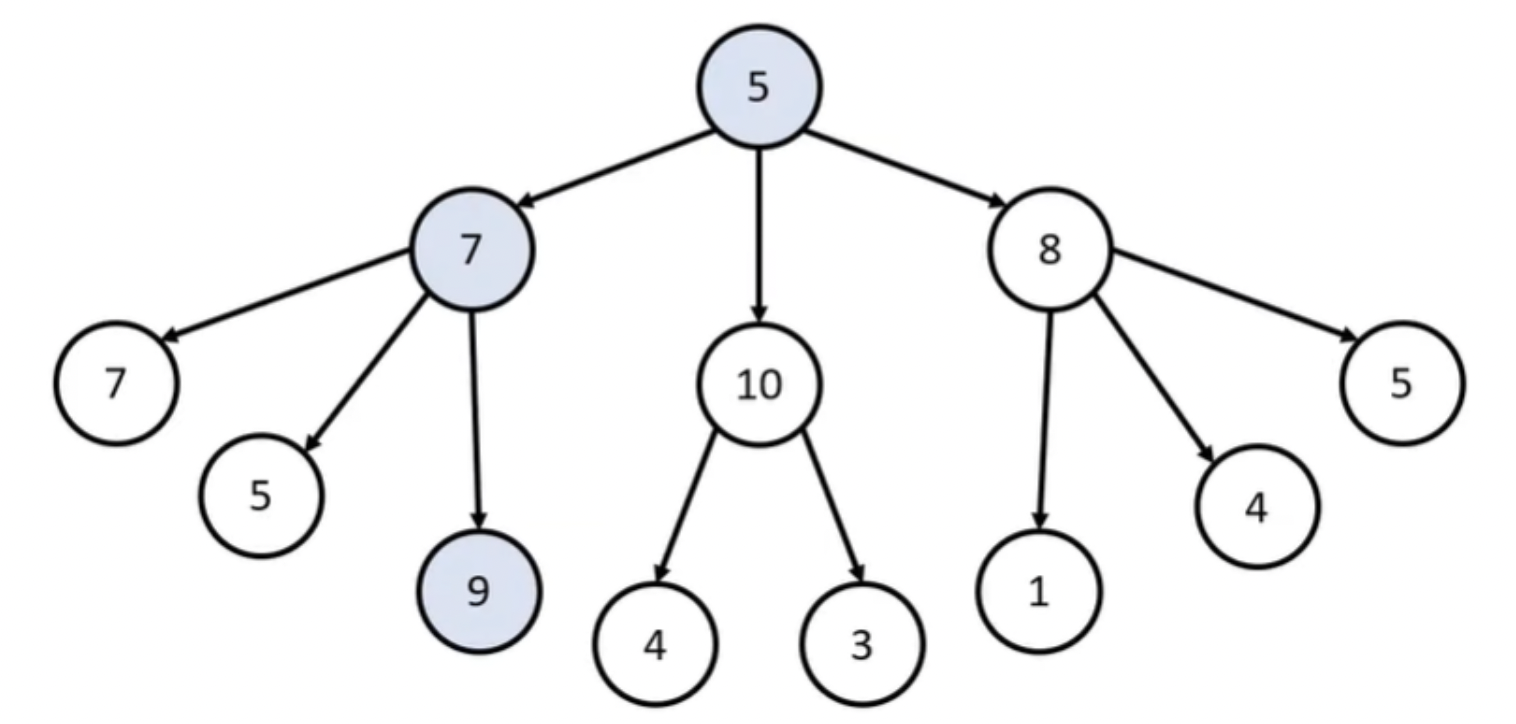
-> 21
Q. 단순히 매 상황에서 가장 큰 값만 고른다면 어떻게 될까요?(그리디 방식)
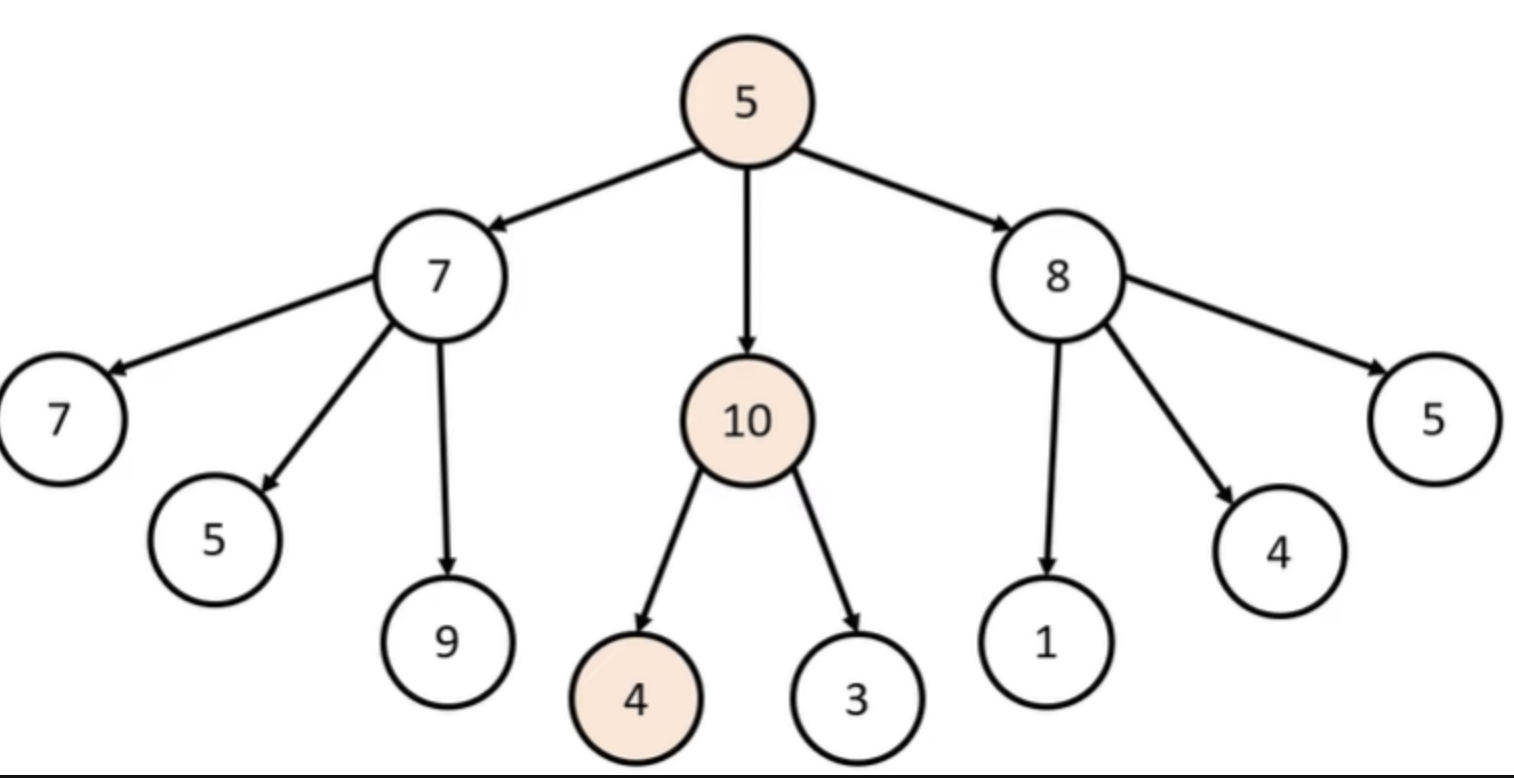
-> 19
- 그리디 알고리즘은 이처럼 매 상황에서 가장 큰 값을 찾아가기는 방식이다.
일반적인 상황에서 그리디 알고리즘은 최적의 해를 보장할 수 없을 때가 많습니다.
하지만 코딩 테스트에서의 대부분의 그리디 문제는 탐욕법으로 얻은 해가 최적의 해가 되는 상황에서, 이를 추론할 수 있어야 풀리도록 출제됩니다.
문제
거스름 돈
[문제 설명]
당신은 음식점의 계산을 도와주는 점원입니다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한히 존재한다고 가정합니다. 손님에게 거슬러 주어야 할 돈이 N원일 때, 거슬러 주어야 할 동전의 최소 개수를 구하세요. 단, 거슬러 줘야할 돈 N은 항상 10의 배수입니다.(즉, 거슬러주지 못할 경우 없음)
[문제 해결 아이디어]
최적의 해를 빠르게 구하기 위해서는 가장 큰 화폐단위 부터 돈을 거슬러 주면 됩니다.
N원을 거슬러 줘야할때, 가장 먼저 500원으로 거슬러 줄 수 있을 만큼 거슬러 줍니다.
-> 이후에 100원, 50원, 10원짜리 동전을 차례대로 거슬러 줄 수 있을 만큼 거슬러 주면 됩니다.
[정당성 분석]
가장 큰 화폐 단위부터 돈을 거슬러 주는 것이 최적의 해를 보장하는 이유는 무엇일까요?
가지고 있는 동전 중에서 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 동전들을 종합해 다른 해가 나올 수 없기 때문입니다.
예시)만약에 800원을 거슬러 주어야 하는데 화폐 단위가 500원, 400원, 100원이라면 어떻게 될까요?
그리디 방식이라면 500원-1개, 100원-3개=> 총 4개이지만,
400원-2개 => 총 2개가 최적의 해이다.(400원이 500원의 배수가 아니기 때문에 발생한 문제)
그리디 알고리즘 문제에서는 이처럼 문제 풀이를 위한 최소한의 아이디어를 떠올리고 이것이 정당한지 검토할 수 있어야 합니다.
[시간 복잡도 분석]
화폐의 종류가 K라고 할 때, 소스코드의 시간 복잡도는 O(K)입니다.
이 알고리즘의 시간 복잡도는 거슬러줘야 하는 금액과는 무관하며, 동전의 총 종류에만 영향을 받습니다.
1이 될 때까지
[문제 설명]
어떠한 수 N이 1이 될 때까지 다음의 두 과정 중 하나를 반복적으로 선택하여 수행하려고 합니다. 단, 두 번째 연산은 N이 K로 나누어 떨어질 때만 선택할 수 있습니다.
N에서 1을 뺍니다.
N을 K로 나눕니다.
예를 들어 N이 17, K가 4라고 가정합시다. 이때 1번의 과정을 한 번 수행하면 N은 16이 됩니다. 이후에 2번의 과정을 두 번 수행하면 N은 1이 됩니다. 결과적으로 이 경우 전체 과정을 실행한 횟수는 3이 됩니다. 이는 N을 1로 만드는 최소 횟수입니다.
N과 K가 주어질 때 N이 1이 될 때까지 1번 혹은 2번의 과정을 수행해야 하는 최소 횟수를 구하는 프로그램을 작성하세요.
[문제 분석]
- 주어진 N에 대하여 최대한 많이 나누기를 수행하면 됩니다.
- N의 값을 줄일 때 2 이상의 수로 나누는 작업을 1을 빼는 작업보다 전체 연산의 횟수를 훨씬 많이 줄일 수 있습니다.
[정당성 분석]
가능하면 최대한 많이 나누는 작업이 최적의 해를 항상 보장할 수 있을까요?
- N이 아무리 큰 수여도, K로 계속 나눈다면 기하급수적으로 빠르게 줄일 수 있습니다.
- 다시 말해 K가 2 이상이기만 하면, K로 나누는 것이 1을 뺴는 것보다 항상 빠르게 N을 줄일 수 있습니다.
- 또한 N은 항상 1에 도달하게 됩니다.(최적의 해 성립)
곱하기 혹은 더하기
[문제 설명]
- 각 자리가 숫자(0부터 9)로만 이루어진 문자열 S가 주어졌을 때, 왼쪽부터 오른쪽으로 하나씩 모든 숫자를 확인하며 숫자 사이에 'x'혹은 '+' 연산자를 넣어 결과적으로 만들어질 수 있는 가장 큰 수를 구하는 프로그램을 작성하세요. 단, +보다 x를 먼저 계산하는 일반적인 방식과는 달리, 모든 연산은 왼쪽에서 부터 순서대로 이루어진다고 가정합니다.
- 예를 들어 02984라는 문자열로 만들 수 있는 가장 큰 수는 ((((0 + 2) x 9) x 8) x 4) = 576입니다. 또한 만들어질 수 있는 가장 큰 수는 항상 20억 이하의 정수가 되도록 입력이 주어집니다.(프로그래밍 언어에서 정수가 가질 수 있는 최대 범위가 약 -2147000000 ~ 2147000000까지 이므로)
{문제 해결 아이디어]
- 대부분의 경우 '+'보다는 'x'가 더 값을 크게만듭니다.
- 예를 들어 5 + 6 = 11이고, 5 x 6 = 30입니다.
- 다만 두 수 중에서 하나라도 '0' 혹은 '1'인 경우, 곱하기 보다는 더하기를 수행하는 것이 효율적입니다. - 따라서 두 수에 대하여 연산을 수행할 때, 두 수중에서 하나라도 1 이하인 경우에는 더하며, 두 수가 모두 2 이상인 경우에는 곱하면 정답입니다.
모험가 길드
[문제 설명]
- 한 마을에 모험가가 N명 있습니다. 모험가 길드에서는 N명의 모험가를 대상으로 '공포도'를 측정했는데, '공포도'가 높은 모험가는 쉽게 공포를 느껴 위험 상황에서 제대로 대처할 능력이 떨어집니다.
- 모험가 길드장인 길동이는 모험가 그룹을 안전하게 구성하고자 공포도가 X인 모험가는 반드시 X명 이상으로 구성한 모험가 그룹에 참여해야 여행을 떠날 수 있도록 규정했습니다.
- 길동이는 최대 몇 개의 모험가 그룹을 만들 수 있는지 궁금합니다. N명의 모험가에 대한 정보가 주어졌을 때, 여행을 떠날 수 있는 그룹의 수의 최댓값을 구하는 프로그램을 작성하세요.
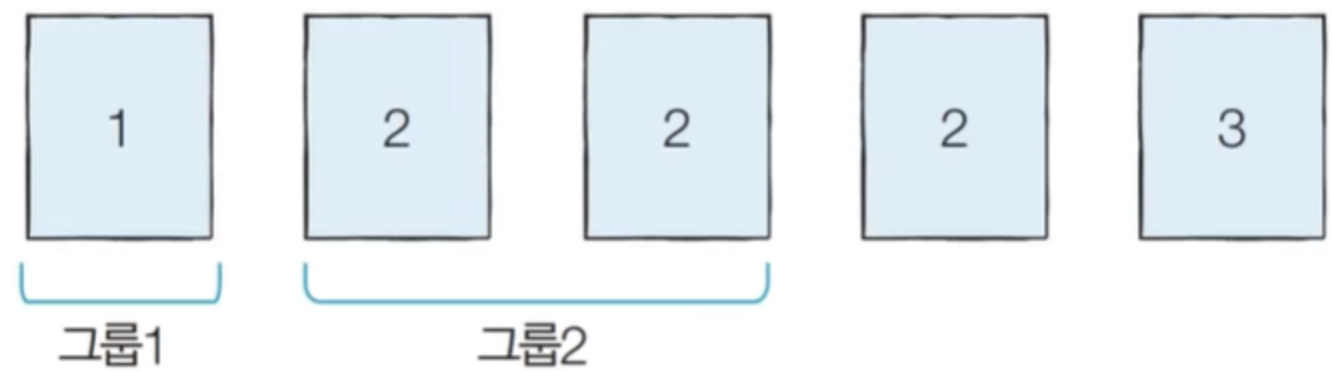
예를 들어 N=5이고, 각 모험가의 공포도가 다음과 같다고 가정합시다.
2 3 1 2 2
- 이 경우 그룹 1에 공포도가 1, 2, 3인 모험가를 한 명씩 넣고, 그룹 2에 공포도가 2인 남은 두명을 넣게 되면 총 2개의 그룹을 만들 수 있습니다.
- 또한 몇 명의 모험가는 마을에 그대로 남아 있어도 되기 때문에, 모든 모험가를 특정한 그룹에 넣을 필요는 없습니다.
[문제 해결 아이디어]
-
오름차순 정렬 이후에 공포도가 가장 낮은 모험가 부터 하나씩 확인합니다.
-
앞에서부터 공포도를 하나씩 확인하며 '현재 그룹에 포함된 모험가의 수'가 '현재 확인하고 있는 공포도'보다 크거나 같다면 새로운 그룹을 설정하면 됩니다.
-
이러한 방법을 이용하면 공포도가 오름차순으로 정렬되어 있다는 점에서, 항상 최소한의 모험가의 수만 포함하여 그룹을 결성하게 됩니다.
[딥안]
n = int(input())
data = list(map(int, input().split()))
data.sort()
result = 0 # 총 그룹의 수
count = 0 # 현재 그룹에 포함된 모험가의 수
for x in data: # 공포도를 낮은 것부터 하니씩 확인하며
count += 1 # 현재 그룹에 해당 모험가를 포함시키기
if count >= x: # 현재 그룹에 포함된 모험가의 수가 현재의 공포도 이상이라면, 그룹 결성o
result += 1 # 총 그룹의 수 증가시키키
count = 0 # 현재 그룹에 모함된 모헌가의 수 초기화
print(result) # 총 그룹의 수 출력구현: 시뮬레이션과 완전 탐색
구현(Implementation)
구현이란, 머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정입니다.
흔히 알고리즘 대회에서 구현 유형의 문제란 무엇을 의미할까요?
- 풀이를 떠올리는 것은 쉽지만 소스코드로 옮기기 어려운 문제를 지칭합니다.
구현 유형의 예시는 다음과 같습니다.
- 알고리즘은 간단한데 코드가 지나칠 만큼 길어지는 문제
- 실수 연산을 다루고, 특정 소수점 자리까지 출력해야 하는 문제
- 문자열을 특정한 기준에 따라서 끊어 처리해야 하는 문제
- 적절한 라이브러리를 찾아서 사용해야 하는 문제
일반적으로 알고리즘 문제에서의 2차원 공간은 행렬(Matrix)의 의미로 사용됩니다.
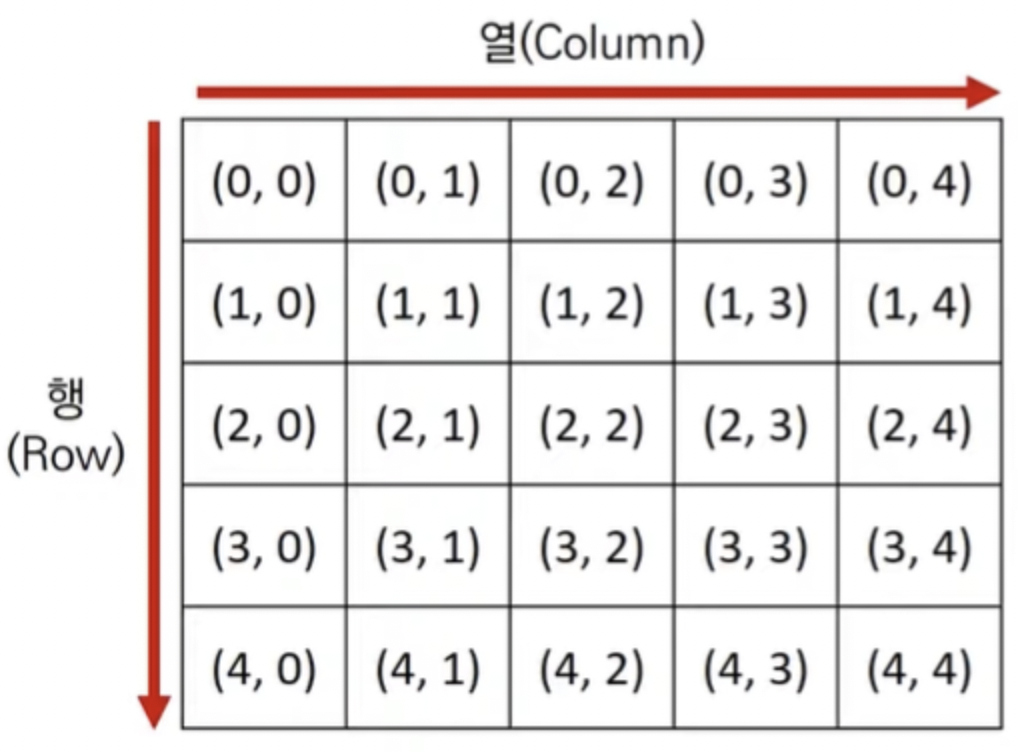
for i in range(5): # 행
for j in range(5): # 열
print('(', i, ',', j, ')', end=' ')
print()시뮬레이션 및 완전 탐색 문제에서는 2차원 공간에서의 방향 벡터가 자주 활용됩니다.
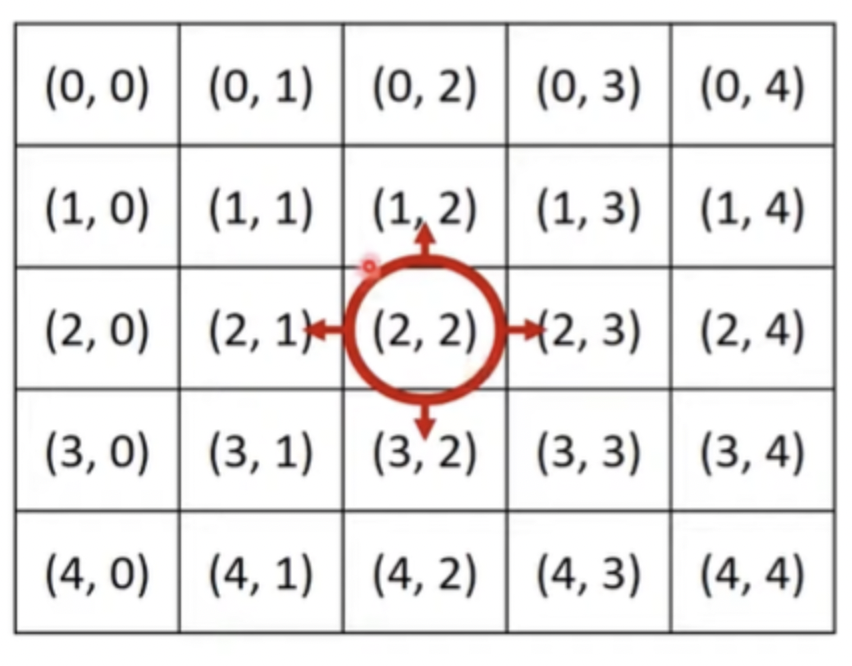
# 동, 북, 서, 남
dx = [0, -1, 0, 1]
dy = [1, 0, -1, 0]
#현재 위치
x, y = 2, 2
for i in range(4):
# 다음 위치
nx = x + dx[i]
ny = y + dy[i]
print(nx, ny)[문제4(구현 중 시뮬레이션 유형)] 상하좌우
[문제 설명]
여행가 A는 N x N 크기의 정사각형 공간 위에 서 있습니다. 이 공간은 1 x 1크기의 정사각형으로 나누어져 있습니다. 가장 왼쪽 위 좌표는 (1, 1)이며, 가장 오른쪽 아래 좌표는 (N, N)에 해당합니다. 여행가 A는 상, 하, 좌, 우 방향으로 이동할 수 있으며, 시작 좌표는 항상 (1, 1)입니다. 우리 앞에는 여행가 A가 이동할 계획이 적힌 계획서가 놓여 있습니다.
계획서에는 하나의 줄에 띄어쓰기를 기준으로 하여 L, R, U, D 중 하나의 문자가 반복적으로 적혀 있습니다. 각 문자의 의미는 다음과 같습니다.
- L: 왼쪽으로 한 칸 이동
- R: 오른쪽으로 한 칸 이동
- U: 위쪽으로 한 칸 이동
- D: 아래쪽으로 한 칸 이동
이때 여행가 A가 N x N크기의 정사각형 공간을 벗어나는 움직임은 무시됩니다.
예를 들어 (1, 1)의 위치에서 L 혹은 U를 만나면 무시됩니다.
[문제 해결 아이디어]
이 문제는 요구사항대로 충실히 구현하면 되는 문제입니다.
- 일련의 명령에 따라서 개체를 차례대로 이동시킨다는 점에서 시뮬레이션(Simulation) 유형으로도 분류되며 구현이 중요한 대표적인 문제 유형입니다.
- 다만, 알고리즘 교재나 문제 풀이 사이트에 따라서 다르게 일컬을 수 있으므로, 코딩 테스트에서의 시뮬레이션 유형, 구현 유형, 완전 탐색 유형은 서로 유사한 점이 많다는 정도로만 기억합시다.
[문제5] 시각
[문제 설명]
정수 N이 입력되면 00시 00분 00초부터 N시 59분 59초까지의 모든 시각 중에서 3이 하나라도 포함되는 모든 경우의 수를 구하는 프로그램을 작성하세요.
예를 들어 1을 입력했을 때 다음은 3이 하나라도 포함되어 있으므로 세어야 하는 시각입니다.
- 00시 00분 03초
- 00시 13분 30초
반면에 다음은 3이 하나도 포함되어 있지 않으므로 세면 안 되는 시각입니다.
- 00시 02분 55초
- 01시 27분 45초
[문제 해결 아이디어]
이 문제는 가능한 모든 시각의 경우를 하나씩 모두 세서 풀 수 있는 문제입니다.
- 하루는 86,400초이므로, 00시 00분 00초부터 23시 59분 59초까지의 모든 경우는 86,400가지 입니다.
- 24 x 60 x 60 = 86,400
따라서 단순히 시각을 1씩 증가시키면서 3이 하나라도 포함되어 있는지를 확인하면 됩니다.
- 이러한 유형은 완전탐색(Brute Forcing) 문제 유형이라고 불립니다.
- 가능한 경우의 수를 모두 검사해보는 탐색 방법(=구현문제)을 의미합니다.
[문제6] 왕실의 나이트
[문제 설명]
행복 왕국의 왕실 정원은 체스판과 같은 8 x 8 좌표 평면입니다.
왕실 정원의 특정한 한 칸에 나이트가 서있습니다. 나이트는 매우 충성스러운 신하로서 매일 무술을 연마합니다.
나이트는 말을 타고 있기 때문에 이동을 할 때는 L자 형태로만 이동할 수 있으며 정원 밖으로는 나갈 수 없습니다.
나이트는 특정 위치에서 다음과 같은 2가지 경우로 이동할 수 있습니다.
- 수평으로 두 칸 이동한 뒤에 수직으로 한 칸 이동하기
- 수직으로 두 칸 이동한 뒤에 수평으로 한 칸 이동하기
8 x 8 좌표 평면상에서 나이트의 위치가 주어졌을 때 나이트가 이동할 수 있는 경우의 수를 출력하는 프로그램을 작성하세요.
왕실의 정원에서 행 위치를 표현할 때는 1부터 8로 표현하며, 열 위치를 표현할 때는 a부터 h로 표현합니다.
c2에 있을 때 이동할 수 있는 경우의 수는 6가지 입니다.
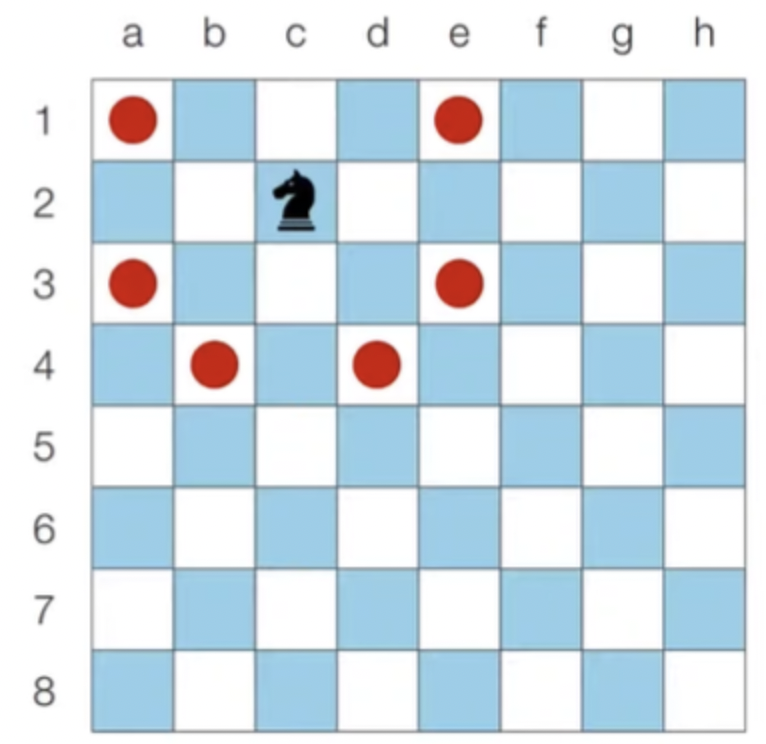
[문제 해결 아이디어]
이 문제는 전형적인 시뮬레이션 완전탐색 문제 유형이면서도 2차원 좌표를 이용하는 구현문제로 볼 수 있습니다.
- 이 문제는 구현문제로써 주어진 요구사항대로 충실히 구현하면 되는 문제입니다.
- 나이트의 8가지 경로를 하나씩 확인하며 각 위치로 이동이 가능한지 확인합니다.
- 리스트를 이용하여 8가지 방향에 대한 벡터를 정의합니다.
[문제 7] 문자열 재정렬
[문제 설명]
알파벳 대문자와 숫자(0~9)로만 구성된 문자열이 입력으로 주어집니다. 이때 모든 알파벳을 오름차순으로 정렬하여 이어서 출력한 뒤에, 그 뒤에 모든 숫자를 더한 값을 이어서 출력합니다.
- 예를 들어 K1KA5CB7이라는 값이 들어오면 ABCKK13을 출력합니다.
[문제 해결 아이디어]
- 이 문제는 구현문제이므로 주어진 요구사항대로 충실히 구현하면 되는 문제입니다.
- 문자열이 입력되었을 때 문자를 하나씩 확인합니다.
- 숫자인 경우 따로 합계를 계산합니다.
- 알파벳의 경우 별도의 리스트에 저장합니다.
- 결과적으로 리스트에 저장된 알파벳을 정렬해 출력하고, 합계를 뒤에 붙여 출력하면 정답입니다.
출처
https://velog.io/@kyunghwan1207/그리디-알고리즘Greedy-Algorithm-탐욕법
Do it 알고리즘 코딩 테스트 Java편
