조합(Combination)
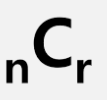
조합은 수학적으로 위와같이 표기한다.
이는 n개 중에서 r개를 뽑는 경우의 수를 뜻한다.
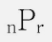
조합과 비교되는 순열은 위와같이 표기하며, 이는 n개 중 r개를 뽑아 순서를 고려해 나열할 경우의 수를 말한다.
순열과 조합의 차이는 순서의 고려 유무이다.
즉, 조합에서는 1,2,3과 3,2,1을 같은 경우로 판단한다.
조합은 코테에서 순열보다 출제 빈도수가 높고, 응용할 수 있는 문제도 많다. 코테에 자주 출제되는 주제이므로 잘 알아두자!
또한 dp를 이해하는데 매우 기초가되는 중요한 개념이다.
순열과 조합의 핵심 이론
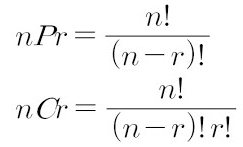
순열과 조합의 공식은 위와같다.
우선 순열 공식을 살펴보자.
예를 들어, 5개 중 2개를 순서대로 선택하는 경우의수를 구한다고 가정해보자.
첫번째 선택에서는 5개 데이터를 선택할 수 있고, 두번째 선택에서는 앞에서 선택한 데이터 1개를 제외한 4개의 데이터를 선택할 수 있다.
따라서 5*4 = 20이된다.
위 수식은 이 내용을 공식화한것이다.
이제 조합을 살펴보자.
순열과 공식이 비슷하나 분모에 r!이 추가돼있는것을 볼 수 있다.
이는 순서가 다른 경우의 수를 제거하는 역할을 한다.
즉. 방금 살펴본 예시에서 1,2를 선택할 때와 2,1을 선택할 때를 한 가지 경우의 수로 만들기위한것이다.
📌 알고리즘에서 조합을 구현할 때는 위의 수학 공식을 코드화하지 않고 점화식을 사용해 표현한다!!
점화식 세우기
5개의 데이터에서 3개의 데이터를 선택하는 조합의 경우의 수를 푸는 문제가있다고 가정하고, 어떤 단계로 점화식을 구해야할지 살펴보자.
1. 모든 부분 문제가 해결된 상황이라고 가정하고 지금 문제 생각하기
모든 부분문제가 해결된 상황이라고 가정해보자.
먼저 5개의 데이터 중 4개를 이미 선택유무를 확정한 데이터라고 가정하는것이다.
그리고 마지막 데이터의 선택 여부에 따른 경우의 수를 계산한다. (물론 마지막 데이터를 선택했는데도 3개안되면 안된다)
(1) 만약 마지막 데이터를 포함해 총 3개의 데이터를 선택하려면 선택 유무를 확정했다고 가정한 4개의 데이터에서 2개를 선택해야한다.
(2) 마지막 데이터를 포함하지않고 총 3개의 데이터를 선택하려면 이전 데이터 4개 중 3개를 선택해야한다.
이렇게 2가지 경우의 수를 합치면 데이터 5개 중 3개를 선택하는 경우의 수가 나온다.
모든 부분 문제가 해결된 상황이라고 가정하는 방법은 조합뿐 아니라 dp에서도 꼭 필요하므로 확실하게 이해하자!!

이 그림을 점화식으로 표현하면 다음과 같다.
<5개 중 3개를 선택하는 경우의 수 점화식>
D[5][3] = D[4][2] + D[4][3]
2. 특정 문제를 해결한 내용을 바탕으로 일반 점화식 도출하기
이 일반화된 점화식을 이용하면 조합과 관련된 모든 경우의 수를 쉽게 구할 수 있다.
<조합 점화식>
D[i][j] = D[i-1][j] + D[i-1][j-1]
이항계수
조합론에서 등장하는 개념이다.
- 주어진 크기 집합에서 원하는 개수만큼 순서없이 뽑는 조합의 가짓수를 일컫는다. 2를 상징하는 ‘이항’이라는 말이 붙은 이유는 하나의 아이템에 대해서는 ‘뽑거나, 안 뽑거나’ 두 가지의 선택만이 있기 때문이다.
전체 집합에서 원소의 개수 n에 대해 k개의 아이템을 뽑는 이항계수(조합의 수)는 다음과 같이 정의한다.
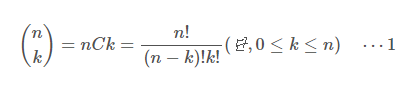
추가적으로 중요한 이항계수의 성질은 다음과 같다.
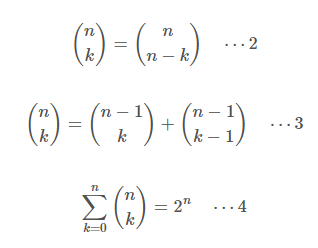
2번은 조금만 생각해보면 상식적이다.
n개 중에서 k개를 간택하는 것은 선택받지 못할 나머지 (n-k)개를 선택하는 것과 같다.
이건 코테에서 시간초과를 유도하는 문제가 나올 수 있다.
경우의수를 구하는 문제인데, 그대로 구현하면 시간초과가 나고, "해당 모든 경우의 수" 에서 "그 어떤 경우의 수가 일어나지 않을 경우의 수"를 뺀 값임을 알아차리고 구현하면 시간초과에서 벗어날 수 있는 문제가 있으므로 유의하자!!
3번은 위에서 살펴본것과 동일하다.
알고리즘을 공부하는 사람이라면 이 식은 기본적으로 외우고 있어야 하는 식이다. 이후 동적 계획법 알고리즘에서 사용할 것이다.
4번은 파스칼의 삼각형과 관련이 깊다.
참고
Do it 알고리즘 코딩 테스트 자바편
https://shoark7.github.io/programming/algorithm/3-ways-to-get-binomial-coefficients
