[자료구조] 트리

Benjamin·2023년 8월 30일
자료구조
0

자료구조

목록 보기
9/9
post-custom-banner

트리

  • 노드로 이루어진 비선형 자료구조
  • 계층적 구조

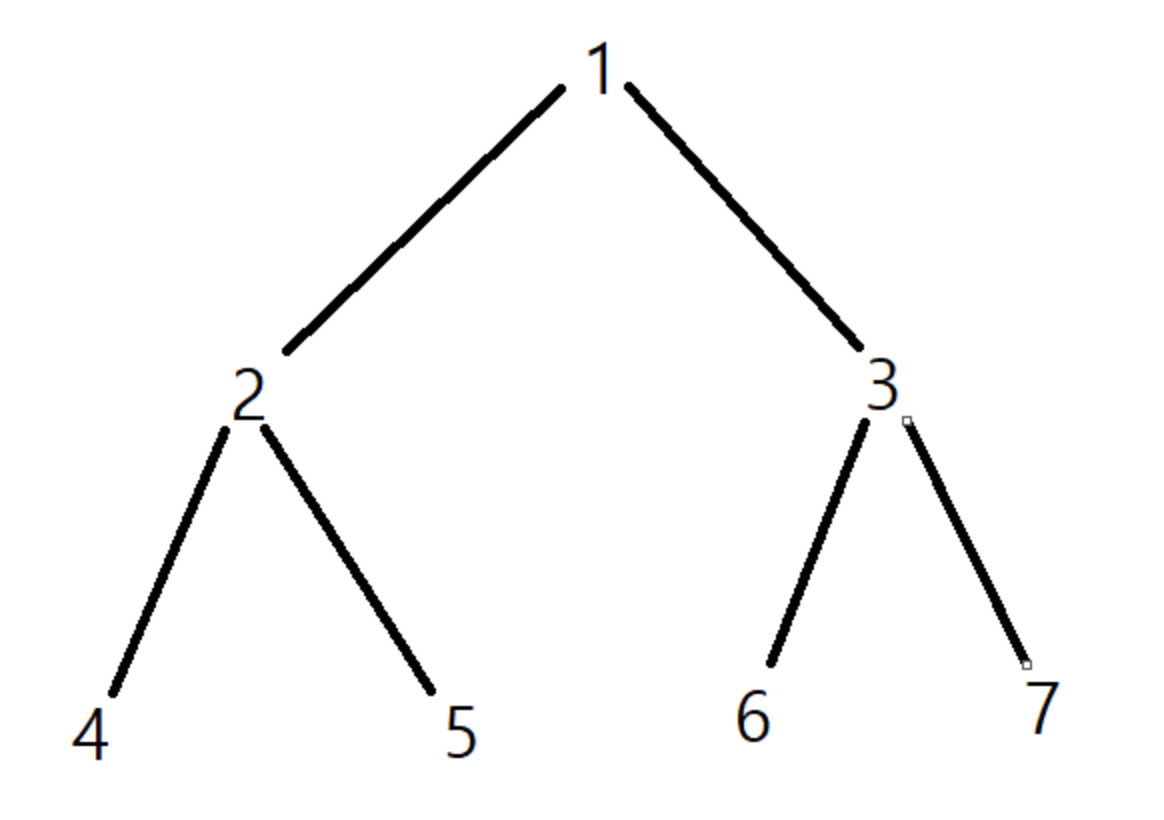
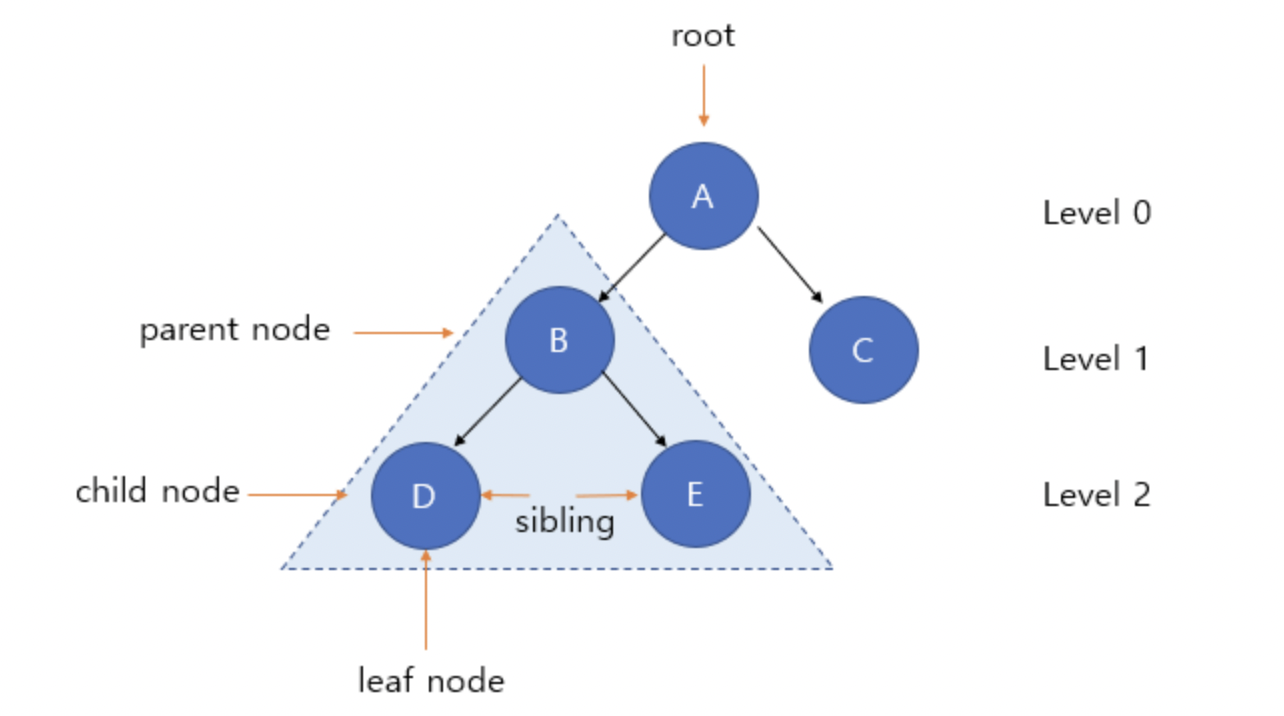
용어

  • 루트(root) : 트리 구조 중 최상위에 존재하는 노드 (1을 가리킴)
  • 노드(node) : 트리에서 각각의 구성 요소
  • 레벨(level) : 트리에서 각각의 층을 나타내는 단어(루트 노드 : 0)
  • 형제 노드(sibling) : 같은 부모 노드를 가지는 모든 노드
  • 간선(edge) : 노드와 노드를 연결하는 선
  • 부모 노드(parent node) : 한 노드를 기준으로 바로 상위에 존재하는 노드
  • 자식 노드(child node) : 한 노드를 기준으로 바로 하위에 존재하는 노드
  • 높이(heigh) : 트리 중 최고 레벨
  • leaf(잎) : 자식이 없는 node
  • subtree : 큰 tree에 속한 작은 tree
  • 노드의 깊이(depth) : 루트 노드에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수(ex : D의 depth : 2)
  • 노드의 차수(degree) : 자식 노드의 개수 ( ex : B의 degree - 2, C의 degree - 0)
  • 트리의 차수(degree of tree) : 트리의 최대 차수 ( ex : 위 트리의 차수는 2이다)

특징

  • 사이클(cycle)이 존재할 수 없다 / 사이클(cycle)이 없는 하나의 연결 그래프(Connected Graph)

  • 트리의 노드는 self-loop가 존재 해서는 안된다.

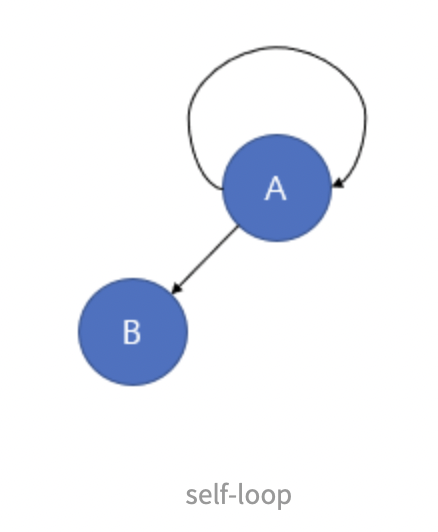
  • N개의 노드를 갖는 트리는 항상 N-1 개의 간선(edge)을 갖는다.

  • 모든 자식 노드는 한 개의 부모 노드만을 갖는다.

처리방법

1.데이터를 저장할 클래스 공간(=노드) 생성

Node 클래스에 3개의 변수를 만든다.

  1. 저장할 값 변수
  2. 왼쪽 연결 노드에 대한 정보를 저장할 변수
  3. 오른쪽 연결 노드에 대한 정보를 저장할 변수
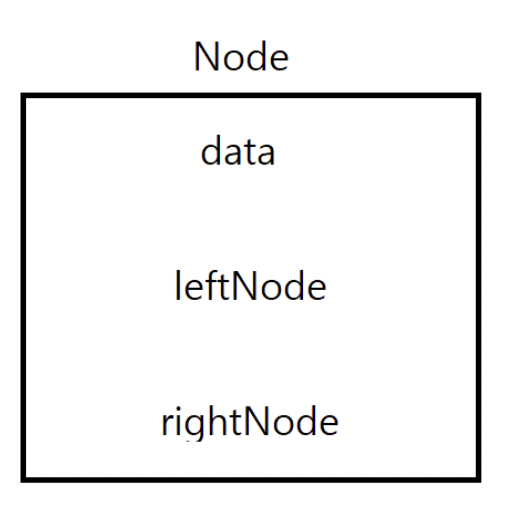
public class Node {
	Object data;
    Node left;
    Node right;
}

2. 각각의 노드에 값 저장

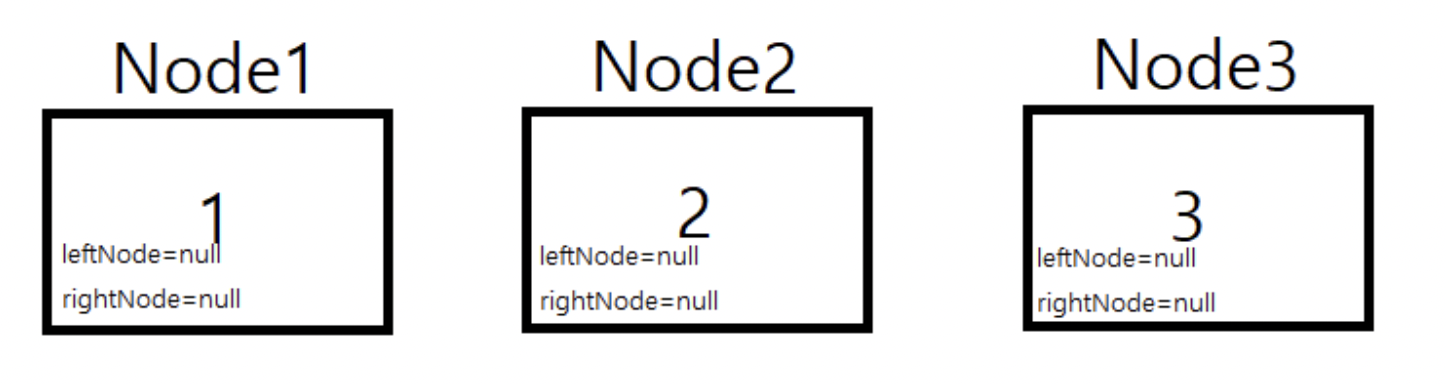
3. 노드 간 연결 상태 정의

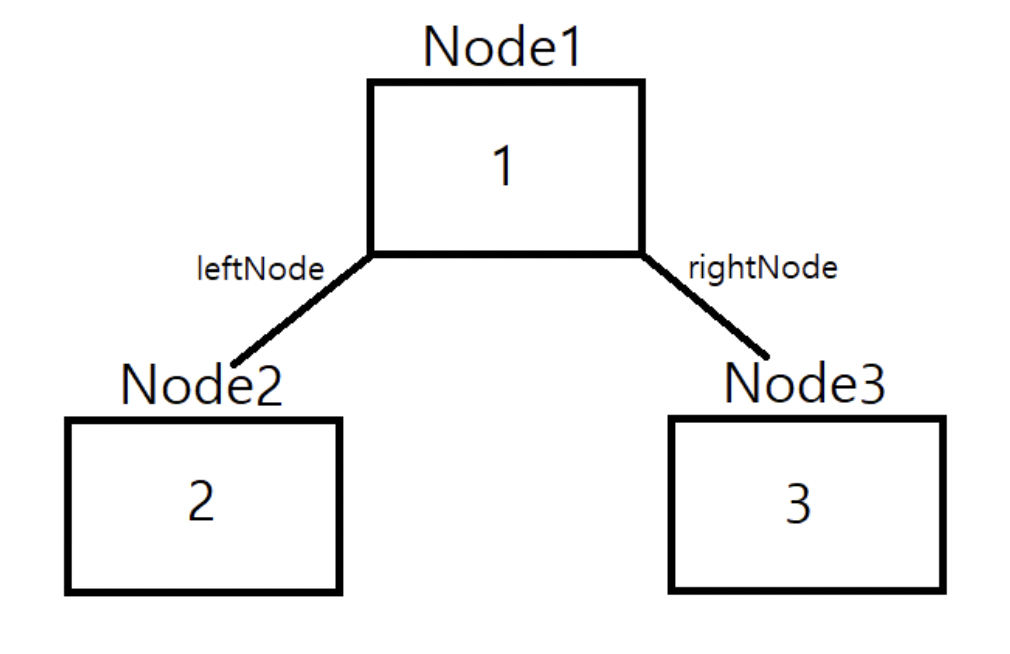위 그림을 코드로 나타내면 아래와 같다.

종류

Binary Tree(이진트리)

  • 자식 노드가 최대 2개인 트리

Complete Binary tree(완전 이진트리)

  • 모든 서브트리의 레벨이 같고, 모든 노드들이 레벨별로 왼쪽부터 채워져있는 경우
  • 마지막 레벨을 제외 하고 모든 레벨이 완전히 채워져 있다.
  • 마지막 레벨은 꽉 차 있지 않아도 되지만, 노드가 왼쪽에서 오른쪽으로 채워져야 한다.

Full Binary Tree (전 이진트리)

  • 노드들이 자식 요소를 두 개를 가지거나, 한개도 가지지 않는 구조

Perfet Binary Tree (포화 이진트리)

  • 양쪽으로 빈 공간 없이 모든 노드가 두개의 자식을 갖고, 레벨도 정확하게 떨어지는 트리
  • 완벽한 파라미드 구조를 형성하고 있음
  • 트리의 높이가 n인 경우, 노드의 개수는 2ⁿ-1 개이다

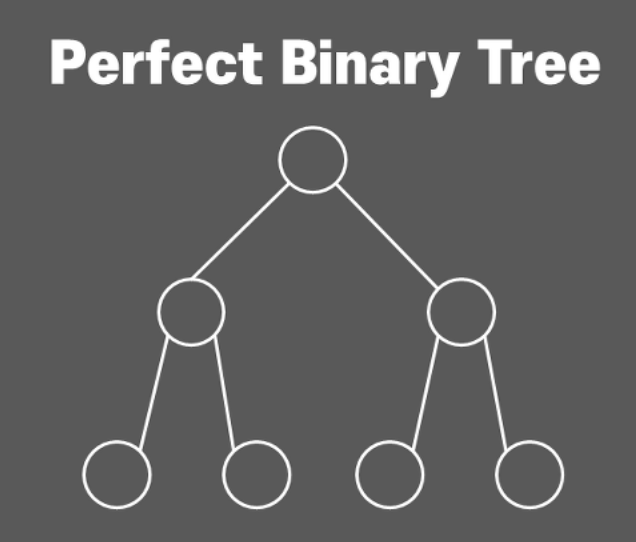
이진 탐색 트리 (BST : Binary Search Tree)

1) 이진 탐색 트리의 노드에 저장된 키(key)는 유일하다.
2) 부모의 키가 왼쪽 자식 노드의 키보다 크다.
3) 부모의 키가 오른쪽 자식 노드의 키보다 작다.
4) 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
5) 최대 2개의 자식을 가진다.

  • 이진 검색 트리의 장점 : 룩업 연산(트리에 있는 특정 노드의 위치를 알아내는 연산)을 빠르고 간단하게 처리할 수 있다.

  • 한단계 올라갈때마다 절반이 줄어들기 때문에, 시간복잡도는 O(log n)이다.

이진 탐색 트리는 효율적인 탐색을 위해 고안된 트리이다.

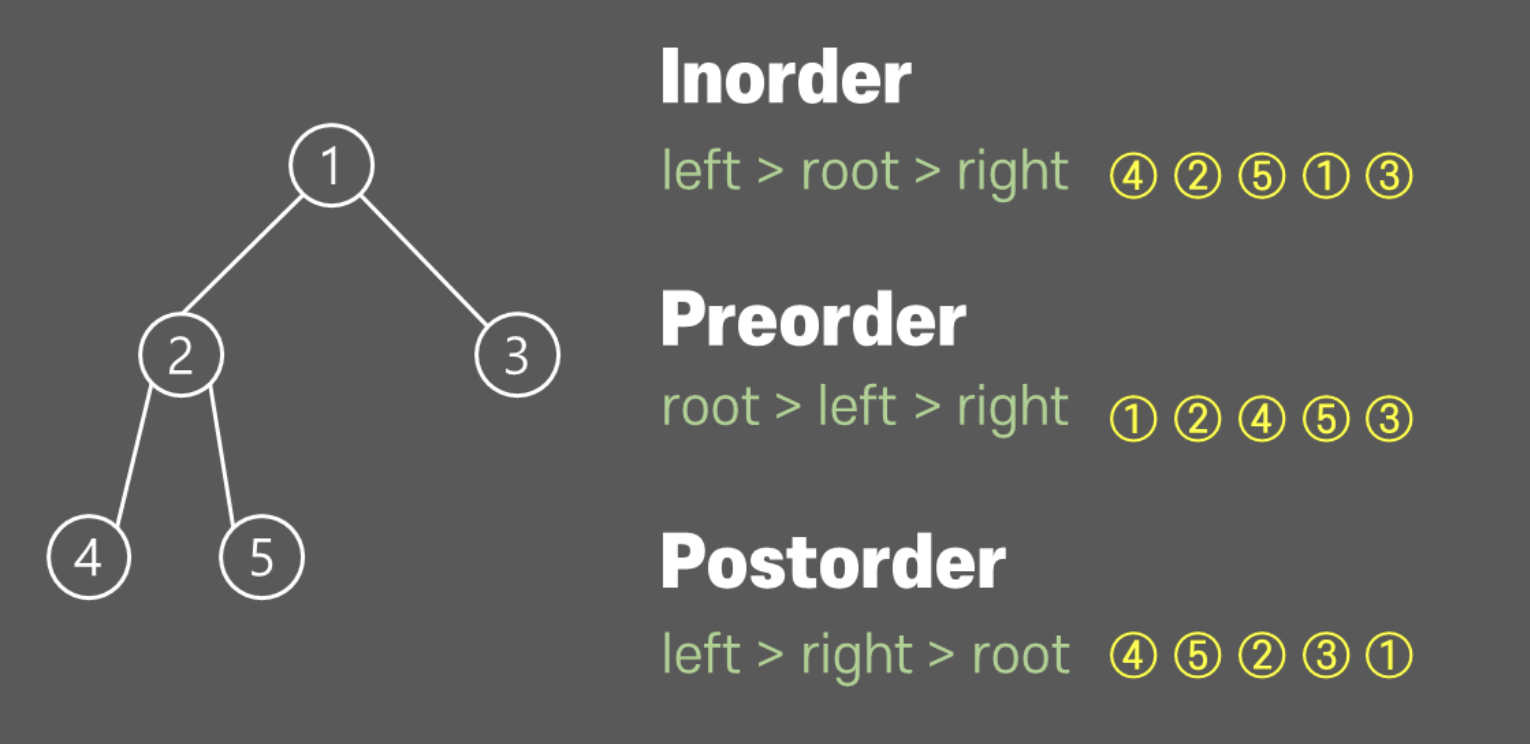
순회방법

전위(pre-order), 중위(in-order), 후위(post-order) 순회가 있다.

  • 전위 순회(pre-order) : root 노드를 먼저 순회한 이후, '왼쪽 -> 오른쪽' 순으로 순회하는 방법.

  • 중위 순회(in-order) : 왼쪽 가장 하위 노드를 먼저 순회한 이후, 'root -> 오른쪽' 순으로 순회하는 방법.

  • 후위 순회(post-order) : 왼쪽 가장 하위 노드를 먼저 순회한 이후, '오른쪽 하위 노드 -> root 노드' 순으로 순회하는 방법

함수

Node

  • void addLeft(Node node)

    현재 노드의 좌측에 노드 연결 정보를 추가한다.

  • void addRight(Node node)

    현재 노드의 우측에 노드 연결 정보를 추가한다.

  • void deleteLeft()

    현재 노드의 좌측 노드 연결 정보를 삭제한다.

  • void deleteRight()

    현재 노드의 좌측 노드 연결 정보를 삭제한다.

Tree

  • Node addNode(Object data)

    노드를 새롭게 생성한다.(저장될 데이터는 data 변수 안에 존재하는 값)

  • void preOrder(Node node)

    전위 순회 방법을 이용해 출력한다.

  • void inOrder(Node node)

    중위 순회 방법을 이용해 출력한다.

  • void postOrder(Node node)

    후위 순회 방법을 이용해 출력한다.

    구현

    Tree 클래스 (Node 포함)

public class Tree {
	int count;
	
	public Tree() {
		count = 0;
	}
	
	public class Node {
		Object data;
		Node left;
		Node right;
	
		// 생성 시 매개변수를 받아 초기화하는 방법으로만 선언 가능
		public Node(Object data) {
			this.data = data;
			left = null;
			right = null;
		}
 
		public void addLeft(Node node) {
			left = node;
			count++;
		}
 
		public void addRight(Node node) {
			right = node;
			count++;
		}
 
		public void deleteLeft() {
			left = null;
			count--;
		}
 
		public void deleteRight() {
			right = null;
			count--;
		}
	}
	
	public Node addNode(Object data) {
		Node n = new Node(data);
		return n;
	}
	
	public void inorder(Node node) {
	// node가 null이 아닐 때까지 재귀호출 반복    
        if(node != null) {  
	// left node 재귀호출을 다 돌고난 후 > 자기 자신 출력 > right node 재귀호출     
            inorder(node.left); 
            System.out.println(node.data);  
            inorder(node.right);
        }
    }
    
    public void preorder(Node node) {
	// node가 null이 아닐 때까지 재귀호출 반복    
        if(node != null) {  
	// 자기 자신 출력 > left node 재귀호출을 다 돌고난 후 > right node 재귀호출     
            System.out.println(node.data);
            preorder(node.left); 
            preorder(node.right);
        }
    }
    
    public void postorder(Node node) {
	// node가 null이 아닐 때까지 재귀호출 반복    
        if(node != null) {  
	// left node 재귀호출을 다 돌고난 후 > right node 재귀호출 > 자기 자신 출력 
            postorder(node.left);
            postorder(node.right); 
            System.out.println(node.data); 
        }
}

실행 클래스

import Tree.*;
import Tree.Tree.Node;
 
public class Run {
	public static void main(String[] args) {
		// 트리 생성
		Tree tree = new Tree();
		
		// 노드 생성
		Node node1 = tree.addNode(1);
		Node node2 = tree.addNode(2);
		Node node3 = tree.addNode(3);
		Node node4 = tree.addNode(4);
		Node node5 = tree.addNode(5);
		Node node6 = tree.addNode(6);
		Node node7 = tree.addNode(7);
		
		// 트리 연결관계 생성
		/*  트리 모양       
		 *        1
		 *     2     3
		 *   4  5  6   7
		 */
		node1.addLeft(node2);
		node1.addRight(node3);
		node2.addLeft(node4);
		node2.addRight(node5);
		node3.addLeft(node6);
		node3.addRight(node7);
		
		// 순회
		tree.preOrder(node1);
		System.out.println();
		tree.inOrder(node1);
		System.out.println();
		tree.postOrder(node1);
		System.out.println();
		
		// 삭제
		node2.deleteLeft();
		node3.deleteRight();
		/* 삭제 이후 트리 모양
		 *        1
		 *     2     3
		 *      5  6   
		 */
		
		// 순회
		System.out.println();
		tree.preOrder(node1);
		System.out.println();
		tree.inOrder(node1);
		System.out.println();
		tree.postOrder(node1);
		System.out.println();
	}
}

참고
https://readerr.tistory.com/35
https://haenny.tistory.com/345#google_vignette
https://code-lab1.tistory.com/8

profile
Benjamin
이전 포스트

[자료구조] HashMap - 개념 및 구현

post-custom-banner

0개의 댓글