• 우선 순위 큐를 위하여 만들어진 자료구조

우선순위 큐는 배열, 연결리스트, 힙으로 구현 가능 : 힙으로 구현하는것이 가장 효율적

힙(heap)이란?

• 완전 이진 트리의 일종

• 여러 개의 값들 중 최댓값 혹은 최솟값을 빠르게 찾아내도록 만들어진 완전이진트리

• 일종의 반정렬 상태(느슨한 정렬 상태)를 유지
  -> 큰 값이 상위 레벨에 있고, 작은 값이 하위 레벨에 있다는 정도
  -> 간단히 말하면 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리

• 중복값을 허용

• 주로 프림알고리즘이나 다익스트라에서 쓰인다.

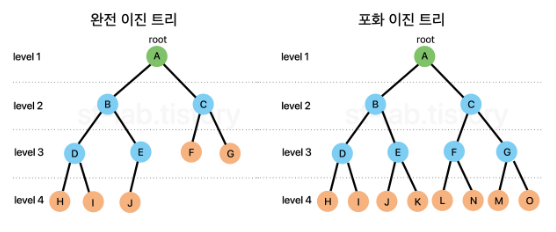
  이진트리(Binary Tree) ?
  모든 노드의 최대 차수를 2로 제한한 것 = 노드는 자식노드를 최대 2개까지밖에 못갖는 것

완전 이진 트리(complete binary tree)?
1. 마지막 레벨을 제외한 모든 노드가 채워져있어야함
2. 모든 노드들은 왼쪽부터 채워져있어야함

포화 이진 트리(perfect binary tree)?
완전 이진 트리 조건 + 마지막 레벨을 제외한 모든 노드는 두 개의 자식노드를 갖는다

반정렬 상태?
이진 트리는 부모노드와 자식노드간의 관계만 신경쓰면 되기 때문에 형제 간 우선순위는 고려되지 않는다.
이러한 정렬 상태를 흔히 '반 정렬 상태' 혹은 '느슨한 정렬 상태' , '약한 힙(weak heap)이라고도 한다.

정렬시 매번 새로 들어오는 값을 기존 원소들과 비교하고 정렬하는것을 효율이 좋게 만들기위해 다음과 같은 조건을 붙였다.
'부모 노드는 항상 자식 노드보다 우선순위가 높다.'

즉, 모든 요소들을 고려하여 우선순위를 정할 필요 없이 부모 노드는 자식노드보다 항상 우선순위가 앞선다는 조건만 만족시키며 완전이진트리 형태로 채워나가는 것이다.
즉, 루트 노드(root node)는 항상 우선순위가 높은 노드라는 것이다.

시간 복잡도

이러한 원리로 최댓값 혹은 최솟값을 빠르게 찾아낼 수 있다는 장점(시간복잡도 : O(1))과 함께 삽입, 삭제 연산시에도 부모노드가 자식노드보다 우선순위만 높으면 되므로 결국 트리의 깊이만큼만 비교를 하면 된다.
따라서 O(logN)의 시간복잡도로 매우 빠르게 수행할 수 있다.

종류

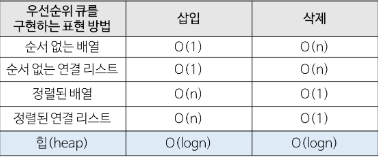
최대 힙(max heap)

• 부모 노드 키 값이 자식 노드 키 값보다 크거나 같은 완전 이진 트리

최소 힙(min heap)

• 부모 노드 키 값이 자식 노드 키 값보다 작거나 같은 완전 이진 트리

구현에 관련해서 아래 블로그에서 너무 자세하게 잘 정리해뒀다..👍
이하 내용은 블로그 내용을 참고해도좋다!
참고블로그

구현

힙을 저장하는 표준적인 자료구조는 배열이다.

물론 연결리스트로도 구현이 가능하긴 하지만, 문제는 특정 노드의 '검색', '이동' 과정이 조금 더 번거롭기 때문이다.
배열의 경우는 특정 인덱스에 바로 접근할 수가 있기 때문에 좀 더 효율적이기도 하다.

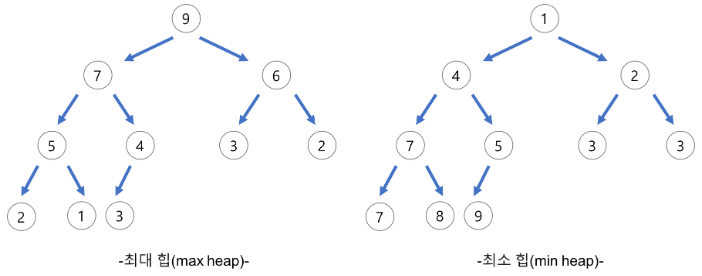
• 특정 위치 노드 번호는 새로운 노드가 추가되어도 변하지 않는다
• 구현의 용이함을 위해 시작 인덱스(root)는 1 부터 시작한다.
• 힙 노드에서 부모노드와 자식노드의 관계
  -> 왼쪽 자식 인덱스 : 부모 인덱스 2
  -> 오른쪽 자식 인덱스 : 부모 인덱스2 +1
  -> 부모 인덱스 : 자식 인덱스 /2

최소힙을 구현하겠다.
최대힙을 구현하고 싶은 경우 비교 연산만 반대로 해주면 된다.

Heap 클래스 및 생성자 구성하기

import java.util.Comparator;
 
public class Heap<E> {
 
	private final Comparator<? super E> comparator;
	private static final int DEFAULT_CAPACITY = 10;	// 최소(기본) 용적 크기 
    
	private int size;	// 요소 개수 
 
	private Object[] array;	// 요소를 담을 배열 
 
	// 생성자 Type 1 (초기 공간 할당 X)
	public Heap() {
		this(null);
	}
	
	public Heap(Comparator<? super E> comparator) {
		this.array = new Object[DEFAULT_CAPACITY];
		this.size = 0;
		this.comparator = comparator;
	}
    
	// 생성자 Type 2 (초기 공간 할당 O)
	public Heap(int capacity) {
		this(capacity, null);
	}
	
	public Heap(int capacity, Comparator<? super E> comparator) {
		this.array = new Object[capacity];
		this.size = 0;
		this.comparator = comparator;
	}
    
 
	// 받은 인덱스의 부모 노드 인덱스를 반환
	private int getParent(int index) {
		return index / 2;
	}
	
	// 받은 인덱스의 왼쪽 자식 노드 인덱스를 반환 
	private int getLeftChild(int index) {
		return index * 2;
	}
	
	// 받은 인덱스의 오른쪽 자식 노드 인덱스를 반환
	private int getRightChild(int index) {
		return index * 2 + 1;
	}
}

<변수의 의미>

• comparator : 여러분들이 객체를 정렬하고자 할 때, 혹은 임의의 순서로 정렬하고 싶을 때 Comparator 를 파라미터로 받아 설정할 수 있도록 한 변수다.
• DEFAULT_CAPACITY : 배열의 기본 및 최소 용적이다. 한마디로 요소를 담을 배열의 크기를 의미한다. 배열을 동적으로 관리 할 때 최소 크기가 10 미만으로 내려가지 않기 위한 변수다. 그리고 요소의 개수랑은 다른 의미이므로 이 점 헷갈리지 말자.
• size : 배열에 담긴 요소(원소)의 개수 변수
• array : 요소를 담을 배열이다.

<생성자를 4개로 나눈 이유>
데이터(요소)의 개수를 예상할 수 있어 배열의 크기(용적)를 최적으로 하고 싶을 때 초기에 생성할 배열의 크기를 설정 해줄 수 있도록 만든 방법과 사용자가 정렬 방법을 따로 넘겨주고자 할 때 쓸 수 있도록 Comparator을 받는 방법을 조합하여 4가지로 나누었다.

resize 메소드 구현

모든 자료구조는 기본적으로 동적으로 만들 수 있어야 한다.

만약 배열에 요소들이 모두 차면 배열의 크기를 늘려야하고, 만약 요소가 배열 용적에 비해 현저히 적으면 낭비되는 메모리가 크므로 적절히 줄여줄 수 있어야 한다.

그럴 때 배열의 크기를 재조정하기 위해 쓰는 메소드다.

/**
 * @param newCapacity 새로운 용적 크기
 */
private void resize(int newCapacity) {
	
	// 새로 만들 배열
	Object[] newArray = new Object[newCapacity];
		
	// 새 배열에 기존에 있던 배열의 요소들을 모두 복사해준다.
	for(int i = 1; i <= size; i++) {
		newArray[i] = array[i];
	}
		
	/*
	 *  현재 배열은 GC 처리를 위해 null로 처리한 뒤, 
	 *  새 배열을 연결해준다.  
	 */
	this.array = null;
	this.array = newArray;
		
}

add 메소드 구현

Heap의 삽입은 크게 두 가지로 나뉜다.

1. 사용자가 Comparator을 사용하여 정렬 방법을 Heap 생성단계에서 넘겨받은 경우 (comparator가 null이 아닌 경우)

2. 클래스 내에 정렬 방식을 Comparable로 구현했거나 기본 정렬 방식을 따르는 경우 (comparator가 null인 경우)

기본적으로 Heap에서 원소가 추가되는 과정을 다음 이미지와 같다.

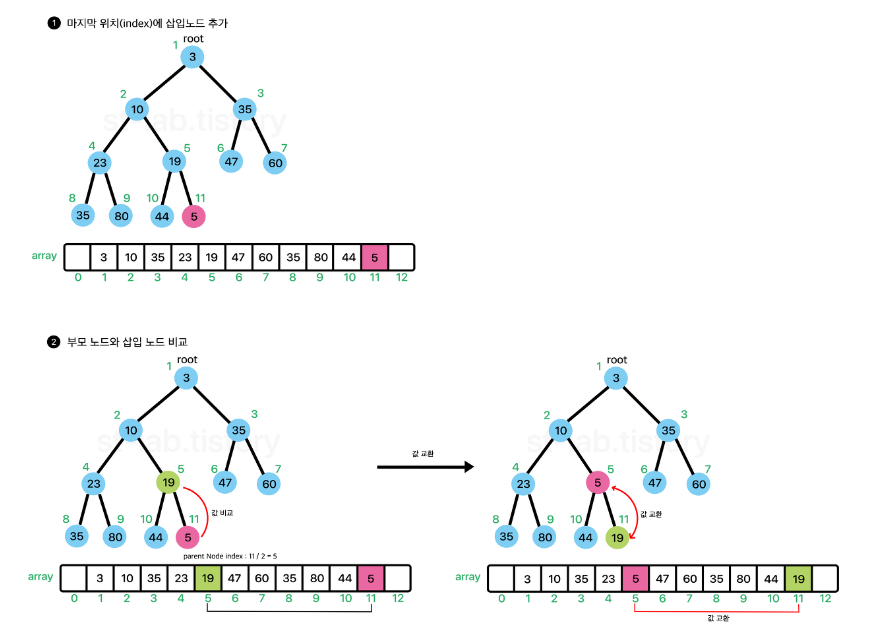
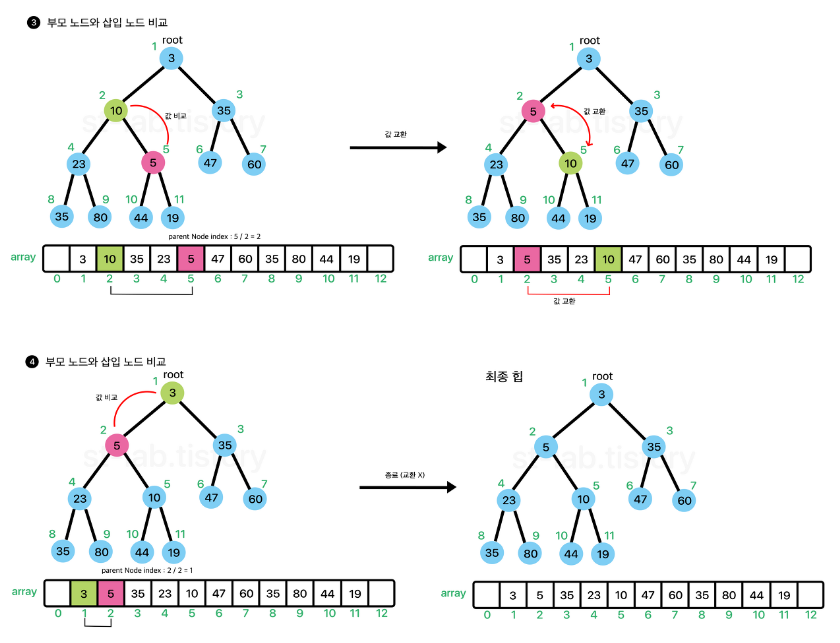
즉, 배열의 마지막 부분에 원소를 넣고 부모노드를 찾아가면서 부모 노드가 삽입 노드보다 작을 때 까지 요소를 교환해가면서 올라간다. 위와 같은 과정을 흔히 위로 올라가면서 선별한다고 하여 sift-up (상향 선별) 이라고도 불린다.

즉, 값을 추가 할 때는 size + 1 위치에 새로운 값을 추가하고 상향 선별 과정을 거쳐 '재배치'를 해준다고 생각하면 된다.

이 때, 재배치 되는 노드를 위 분홍색 노드 즉, 타겟노드(target)라고 생각하면 된다.

public void add(E value) {
		
	// 배열 용적이 꽉 차있을 경우 용적을 두 배로 늘려준다. 
	if(size + 1 == array.length) {
		resize(array.length * 2);
	}
		
	siftUp(size + 1, value);	// 가장 마지막에 추가 되는 위치와 넣을 값(타겟)을 넘겨줌
	size++;	// 정상적으로 재배치가 끝나면 사이즈를 증가
}
	
// 상향 선별
/**
 * @param idx	추가할 노드의 인덱스 
 * @param target	재배치 할 노드
 */
private void siftUp(int idx, E target) {	
	// comparator가 존재할 경우 comparator 을 인자로 넘겨준다.
	if(comparator != null) {
		siftUpComparator(idx, target, comparator);
	}
	else {
		siftUpComparable(idx, target);
	}
}
 
// Comparator을 이용한 sift-up
@SuppressWarnings("unchecked")
private void siftUpComparator(int idx, E target, Comparator<? super E> comp) {		
 
	// root노드보다 클 때까지만 탐색한다.
	while(idx > 1) {
		int parent = getParent(idx);	// 삽입노드의 부모노드 인덱스 구하기
		Object parentVal = array[parent];	// 부모노드의 값
		
		// 타겟 노드 값이 부모노드보다 크면 반복문 종료
		if(comp.compare(target, (E) parentVal) >= 0) {
			break;
		}
			
		/*
		 * 부모노드가 타겟노드보다 크므로
		 * 현재 삽입 될 위치에 부모노드 값으로 교체해주고
		 * 타겟 노드의 위치를 부모노드의 위치로 변경해준다. 
		 */
		array[idx] = parentVal;
		idx = parent;
	}
		
	// 최종적으로 삽입될 위치에 타겟 노드 값을 저장해준다.
	array[idx] = target;
}
 
// 삽입 할 객체의 Comparable을 이용한 sift-up
@SuppressWarnings("unchecked")
private void siftUpComparable(int idx, E target) {
		
	// 타겟노드가 비교 될 수 있도록 한 변수를 만든다. 
	Comparable<? super E> comp = (Comparable<? super E>) target;
		
	while(idx > 1) {
		int parent = getParent(idx);
		Object parentVal = array[parent];
			
		if(comp.compareTo((E)parentVal) >= 0) {
			break;
		}
		array[idx] = parentVal;
		idx = parent;
	}
	array[idx] = comp;
}

일단 요소를 추가하기 전에 추가 할 공간이 있는지를 검사해야 한다. 만약 배열의 길이(용적)가 10이고, 요소의 개수인 size가 9일 경우 배열의 마지막 인덱스까지 꽉 찼다는 의미다. (힙은 index 1부터 채우므로)

그렇기에 용적의 크기를 2배로 늘려 준 뒤, siftUp 메소드를 호출 해준다.

그 다음 앞서 말했던 Comparator로 넘겨받은 것이 있는지, 없는지에 따라 Comparator가 있을 경우 compre()을, 없을 경우 compareTo()를 사용하여 요소를 비교해야 하므로 검사를 한 뒤 각각의 siftUp 메소드로 넘어가 재배치 작업을 해준다.

위와같이 추가해보다보면 알겠지만 결국 '마지막 삽입 되는 인덱스'부터 부모노드를 비교하면서 올라가기 때문에 항상 완전 이진 트리를 만족하면서, 부모노드는 자식노드보다 우선순위가 높다는 것 또한 침해받지 않는다.

그리고 만약 최대힙을 구현하고 싶은 경우 compare 혹은 compareTo에서의 >= 0 비교연산자를 <= 로 바꿔주면 된다.

remove 메소드 구현

remove의 구현은 add와 정반대로 하면 된다.

삭제연산의 경우 root에 있는 노드를 삭제하고, 마지막에 위치해있던 노드를 root Node로 가져와 add와는 반대로 자식노드가 재배치하려는 노드보다 크거나 자식노드가 없을 때 까지 자신의 위치를 찾아가면 된다.

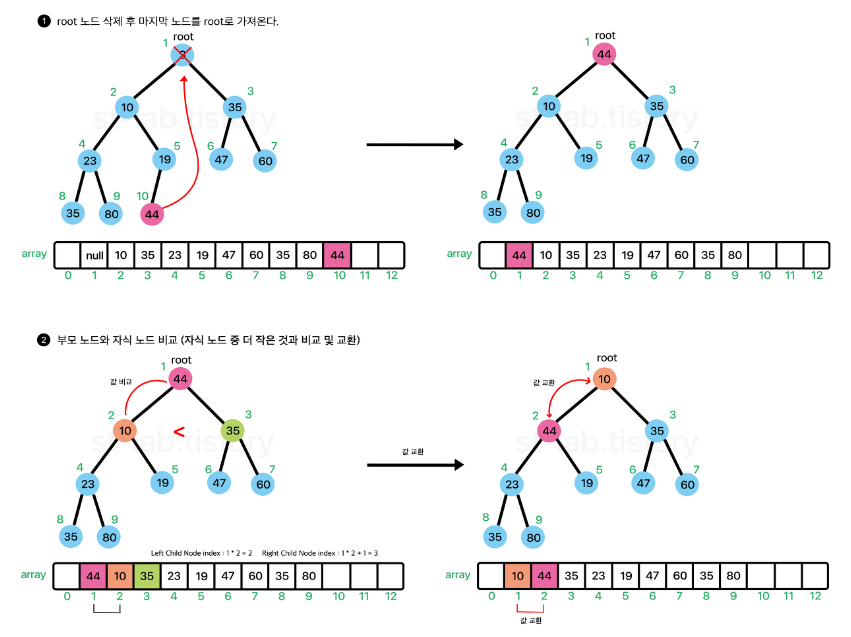
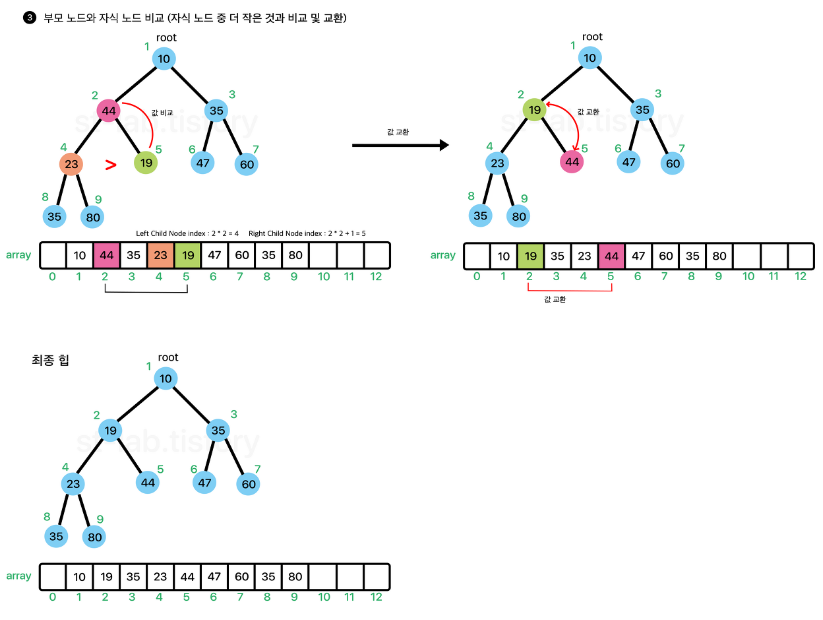
중요한 점은 왼쪽 자식 노드와 오른쪽 자식 노드 중 '작은 값을 가진 노드'랑 재배치 할 노드와 비교해야한다.
이렇게 아래로 내려가면서 재배치 하는 과정을 이러한 과정을 sift-down (하향 선별)이라고도 한다.

그리고 삽입과정과 마찬가지로 Comparator을 쓰느냐, Comparable을 쓰느냐를 나누면서 만들겠다.

@SuppressWarnings("unchecked")
public E remove() {
	if(array[1] == null) {	// 만약 root가 비어있을경우 예외를 던지도록 함
		throw new NoSuchElementException();
	}
    
	E result = (E) array[1];	// 삭제된 요소를 반환하기 위한 임시 변수 
	E target = (E) array[size];	// 타겟이 될 요소
	array[size] = null;	// 타겟 노드를 비운다.
		
	// 삭제할 노드의 인덱스와 이후 재배치 할 타겟 노드를 넘겨준다.
	siftDown(1, target);	// 루트 노드가 삭제되므로 1을 넘겨준다.
		
	return result;
}
	
	
/**
 * @param idx	삭제할 노드의 인덱스 
 * @param target	재배치 할 노드
 */
private void siftDown(int idx, E target) {
	// comparator가 존재할 경우 comparator 을 인자로 넘겨준다.
	if(comparator != null) {
		siftDownComparator(idx, target, comparator);
	}
	else {
		siftDownComparable(idx, target);
	}
}
	
// Comparator을 이용한 sift-down
@SuppressWarnings("unchecked")
private void siftDownComparator(int idx, E target, Comparator<? super E> comp) {
		
	array[idx] = null;	// 삭제 할 인덱스의 노드를 삭제
	size--;	
			
	int parent = idx;	// 삭제노드부터 시작 할 부모를 가리키는 변수
	int child;	// 교환 될 자식을 가리키는 변수
		
	// 왼쪽 자식 노드의 인덱스가 요소의 개수보다 작을 때 까지 반복
	while((child = getLeftChild(parent)) <= size) {
			
		int right = getRightChild(parent);	// 오른쪽 자식 인덱스
			
		Object childVal = array[child];	// 왼쪽 자식의 값 (교환 될 값) 
			
		/*
		 *  오른쪽 자식 인덱스가 size를 넘지 않으면서
		 *  왼쪽 자식이 오른쪽 자식보다 큰 경우
		 *  재배치 할 노드는 작은 자식과 비교해야하므로 child와 childVal을
		 *  오른쪽 자식으로 바꿔준다. 
		 */
		if(right <= size && comp.compare((E) childVal, (E) array[right]) > 0) {
			child = right;
			childVal = array[child];
		}
			
		// 재배치 할 노드가 자식 노드보다 작을경우 반복문을 종료한다. 
		if(comp.compare(target ,(E) childVal) <= 0){
			break;
		}
			
		/*
		 *  현재 부모 인덱스에 자식 노드 값을 대체해주고 
		 *  부모 인덱스를 자식 인덱스로 교체
		 */
		array[parent] = childVal;
		parent = child;
	}
		
	// 최종적으로 재배치 되는 위치에 타겟이 된 값을 넣어준다.
	array[parent] = target;
		
	/*
	 *  용적의 사이즈가 최소 용적보다는 크면서 요소의 개수가 전체 용적의 1/4일경우 
	 *  용적을 반으로 줄임(단, 최소용적보단 커야함)
	 */
	if(array.length > DEFAULT_CAPACITY && size < array.length / 4) {
		resize(Math.max(DEFAULT_CAPACITY, array.length / 2));
	}
 
}
	
// Comparable을 이용한 sift-down
@SuppressWarnings("unchecked")
private void siftDownComparable(int idx, E target) {
		
	Comparable<? super E> comp = (Comparable<? super E>) target;
		
	array[idx] = null;
	size--;
		
	int parent = idx;
	int child;
 
	while((child = getLeftChild(parent)) <= size) {
			
		int right = getRightChild(parent);
			
		Object childVal = array[child];
		
		if(right <= size && ((Comparable<? super E>)childVal).compareTo((E)array[right]) > 0) {
			child = right;
			childVal = array[child];
		}
			
		if(comp.compareTo((E) childVal) <= 0){
			break;
		}
		array[parent] = childVal;
		parent = child;
			
	}
	array[parent] = comp;
		
	if(array.length > DEFAULT_CAPACITY && size < array.length / 4) {
		resize(Math.max(DEFAULT_CAPACITY, array.length / 2));
	}
}

size, peek, isEmpty, toArray 메소드 구현

public int size() {
	return this.size;
}
	
@SuppressWarnings("unchecked")
public E peek() {
	if(array[1] == null) {
		throw new NoSuchElementException();
	}		
	return (E)array[1];
}
 
public boolean isEmpty() {
	return size == 0;
}
 
public Object[] toArray() {
	return Arrays.copyOf(array, size + 1);
}

---

test

import java.util.Random;
 
public class test {
	public static void main(String[] args) {
		
		Heap<Integer> heap = new Heap<>();
		
		Random rnd = new Random();
		
		for(int i = 0; i < 15; i++) {
			heap.add(rnd.nextInt(100));
		}
		
		// 힙 내부 배열의 요소 상태
		System.out.print("내부 배열 상태 : ");
		for(Object val : heap.toArray()) {
			System.out.print(val + " ");
		}
		System.out.println();
		
		
		// 힙이 비어있을 때 까지 한 개씩 요소 뽑음
		System.out.print("힙 요소 뽑기 : \t");
		while(!heap.isEmpty()) {
			System.out.print(heap.remove() + " ");
		}
		
	}
 
}

배열을 얻을 때 index 1부터 시작하기 때문에 내부 배열상태에서 맨 첫번 째가 null이 나오는 것은 정상이다.

사용자 정의 클래스일 경우 테스트

import java.util.Comparator;
 
public class Test {
 
	public static void main(String[] args) {
		
		Heap<Student> heap1 = new Heap<Student>();
		Heap<Student> heap2 = new Heap<Student>(comparator);
 
		
		heap1.add(new Student("김자바", 40));
		heap2.add(new Student("김자바", 40));
		
		heap1.add(new Student("이씨프", 27));
		heap2.add(new Student("이씨프", 27));
		
		heap1.add(new Student("조파이", 48));
		heap2.add(new Student("조파이", 48));
		
		heap1.add(new Student("김자바", 18));
		heap2.add(new Student("김자바", 18));
		
		heap1.add(new Student("상스윕", 32));
		heap2.add(new Student("상스윕", 32));
		
		heap1.add(new Student("양씨샵", 27));
		heap2.add(new Student("양씨샵", 27));
		
		
		System.out.println("[Heap 1] : 이름순(같을 경우 나이 오름차순)");
		while(!heap1.isEmpty()) {
			System.out.println(heap1.remove());
		}
		System.out.println();
		
		System.out.println("[Heap 2] : 나이 내림차순(같을 경우 이름순)");
		while(!heap2.isEmpty()) {
			System.out.println(heap2.remove());
		}
		System.out.println();
	}
	
	private static Comparator<Student> comparator = new Comparator<Student>() {
		@Override
		public int compare(Student o1, Student o2) {
			// 나이가 같다면 이름순
			if(o1.age == o2.age) {
				return o1.name.compareTo(o2.name);
			}
			
			return o2.age - o1.age;	// 나이 내림차순
		}
	};
	
	private static class Student implements Comparable<Student> {
		
		String name;
		int age;
		
		public Student(String name, int age) {
			
			this.name = name;
			this.age = age;
		}
 
		@Override
		public int compareTo(Student o) {
			// 이름이 같다면 나이순 (오름차순)
			if(this.name.compareTo(o.name) == 0) { 
				return this.age - o.age;
			}
			// 이름순
			return this.name.compareTo(o.name);
			
		}
		
		
		public String toString() {
			return "이름 : " + name + "\t나이 : " + age;
		}
	}
}

참고
https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
https://st-lab.tistory.com/205