합이 같은 부분집합
✏️ 문제
* 설명
N개의 원소로 구성된 자연수 집합이 주어지면, 이 집합을 두 개의 부분집합으로 나누었을 때
두 부분집합의 원소의 합이 서로 같은 경우가 존재하면 “YES"를 출력하고, 그렇지 않으면 ”NO"를 출력하는 프로그램을 작성하세요.
둘로 나뉘는 두 부분집합은 서로소 집합이며, 두 부분집합을 합하면 입력으로 주어진 원래의 집합이 되어 합니다.
예를 들어 {1, 3, 5, 6, 7, 10}이 입력되면 {1, 3, 5, 7} = {6, 10} 으로 두 부분집합의 합이 16으로 같은 경우가 존재하는 것을 알 수 있다.
* 입력
첫 번째 줄에 자연수 N(1<=N<=10)이 주어집니다.
두 번째 줄에 집합의 원소 N개가 주어진다. 각 원소는 중복되지 않는다.
출력
첫 번째 줄에 “YES" 또는 ”NO"를 출력한다.💡
너무 어렵게 생각하려고 하지 말고, 직관적으로 기준을 잡고 진행하자.
(ex:n이 끝까지 갔을 때 확인.) 실행 시간을 조금이라도 아끼려고 매 루트에서 확인을 하려고 하다보니 매우 복잡해진다. (n-1 까지 확인 등도..) 사실 그정도 차이는 크게 차이나지 않는다.
2개의 선택지가 있을 때에는, o, x의 경우를 나눠서 재귀로 2번 보내주면 모든 경우를 탐색한다.
🔍풀이
DFS 방식을 이용해 해결
clas Main {
static String answer = "NO";
static int n, total = 0;
boolean flag = false; //main에서 접근하는 것이 아니기 때문에 static필요 x
public void DFS(int L, int sum, int[] arr){
if(sum > total/2) return;
if(flag == true) return;
if(L == n) {
if(totla - sum == sum) {
answer = "YES";
flag = true;
}
}
else{
DFS(L+1, sum+arr[L], arr);
DFS(L+1, sum, arr);
}
}
public static void main(String[] args){
Main T = new Main();
Scanner sc = new Scanner(Sysytem.in);
int n = sc.nextInt();
int[] arr = new int[n];
for(int i = 0; i < n; i++){
arr[i] = sc.nextInt();
total += arr[i];
}
T.DFS(0, 0, arr);
System.out.println(answer);
}
}강아지 승차
✏️ 문제

🔍풀이
위 문제와 아주 유사한 문제. DFS로 해결할 수 있다는 것을 알아차리기만 하면 된다. 즉, DFS는 모든 경우의 수를 찾아내는 데 최적화 되어있다.
class DFS2 {
static int answer=Integer.MIN_VALUE, c, n;
public void DFS(int L, int sum, int[] arr){
if(sum > c) return;
if(L == n) {
answer = Math.max(sum, answer);
}
else{
DFS(L+1, sum+arr[L], arr);
DFS(L+1, sum, arr);
}
}
최대 점수 구하기
✏️ 문제
* 설명
이번 정보올림피아드대회에서 좋은 성적을 내기 위하여 현수는 선생님이 주신 N개의 문제를 풀려고 합니다.
각 문제는 그것을 풀었을 때 얻는 점수와 푸는데 걸리는 시간이 주어지게 됩니다.
제한시간 M안에 N개의 문제 중 최대점수를 얻을 수 있도록 해야 합니다.
(해당문제는 해당시간이 걸리면 푸는 걸로 간주한다, 한 유형당 한개만 풀 수 있습니다.)
* 입력
첫 번째 줄에 문제의 개수N(1<=N<=20)과 제한 시간 M(10<=M<=300)이 주어집니다.
두 번째 줄부터 N줄에 걸쳐 문제를 풀었을 때의 점수와 푸는데 걸리는 시간이 주어집니다.
* 출력
첫 번째 줄에 제한 시간안에 얻을 수 있는 최대 점수를 출력합니다.🔍풀이
static int m ,n, answer=0;
public void DFS(int time, int score, int L, int[][] q){
if(time > m) return;
if(L == n){
if(score > answer) answer = score;
}else{
DFS(time+q[L][1], score+q[L][0], L+1, q);
DFS(time, score, L+1, q);
}
}
public static void main(String[] args) {
DFS3 T = new DFS3();
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
int[][] q = new int[n][2];
for(int i = 0; i < n; i++){
q[i][0] = sc.nextInt();
q[i][1] = sc.nextInt();
}
T.DFS(0, 0, 0, q);
System.out.println(answer);
}주의사항 : q[][]배열에서 2번째 항의 좌표는 항상 고정되어야 한다.
여기에 변수를 넣으면 안된다. score는 무조건 0. time은 무조건 1.
동전교환
✏️ 문제
* 설명
다음과 같이 여러 단위의 동전들이 주어져 있을때 거스름돈을 가장 적은 수의 동전으로 교환해주려면 어떻게 주면 되는가?
각 단위의 동전은 무한정 쓸 수 있다.
* 입력
첫 번째 줄에는 동전의 종류개수 N(1<=N<=12)이 주어진다. 두 번째 줄에는 N개의 동전의 종류가 주어지고,
그 다음줄에 거슬러 줄 금액 M(1<=M<=500)이 주어진다.각 동전의 종류는 100원을 넘지 않는다.
* 출력
첫 번째 줄에 거슬러 줄 동전의 최소개수를 출력한다.🔍풀이
for문을 통해 재귀함수를 사용하면, 모든 경우의 수를 다 탐색할 수 있다.
public class Main{
static int n, amount, answer = Integer.MAX_VALUE;
public void DFS(int L, int sum, int[] arr){
if(sum > amount || L > answer) return;
if(sum == amount) answer = Math.min(answer, L)
else{
for(int i = n-1; i >= 0; i--){
DFS(L+1, sum+arr[i], arr);
}
}
}
public static void main(String[] args){
Main T = new Main();
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
int[] arr = new int[n];
for(int i = 0; i < n; i++){
arr[i] = sc.nexInt();
}
amount = sc.nextInt();
T.DFS(0, 0, arr);
System.out.println(answer);
}
}주의사항 : '큰 동전부터' 확인하는 것이 가장 빠른 방법이다.
순열구하기

public void DFS(ArrayList<Integer> list){
if(list.size() == m) System.out.println(list);
else{
for(int i = 0; i < n; i++){
if(!list.contains(arr[i])){
list.add(arr[i]);
DFS(list);
list.remove(list.size()-1);
}
}
}
}2번째방법
static int[] pm, ch, arr;
static int n, m;
public void DFS(int L){
if(L==m){
for(int x : px) System.out.print(x + " ");
System.out.println();
}else{
for(int i = 0; i < n; i++){
if(ch[i]==0){
ch[i]=1;
pm[L]=arr[i];
DFS(L+1);
ch[i]=0;
}
}
}
}ch로 해당 원소를 사용했는가? -> list.contains
ch[i] = 0; -> list.remove(list.size()-1);
원리는 같다. 다만 출력하는 과정에서 for문을 통해 반복문을 돌리면,
10개의 수 중 10개를 뽑아 순열을 만드는 과정은 10!인데, (약360만) 이것을 반복문으로 출력하면 3600만 번의 반복을 돌아야 하기 때문에 속도면에서 매우 느림.
조합수(메모이제이션)

public class Main{
int arr[34][34]; // 입력될 수 있는 최대값으로 배치
public int DFS(int n, int r){
if(arr[n][r] != 0) return arr[n][r];
if(n == r || r == 0) return 1;
else return arr[n][r] = DFS(n-1, r) + DFS(n-1, r-1);
// arr[n][r]을 초기화 해주면서, 오른쪽 항의 int값을 return한다.
}
}수열 추측하기

🔍풀이
조합수(메모이제이션)을 먼저 구현하여 combination처리 메소드를 구현한 뒤, 각 항은 차례로 n-1C0, n-1C₁, n-1C₂.. 만큼 더해지므로 두 개의 배열을 곱해서 sum에 담아준다.
public class Main{
static int n, f;
static int[] c, p, ch; // c:combination경우의 수를 담음
// p:검증할 조합된 수들을 담음
int[][] com = new int[11][11];
boolean flag = false;
public int Combi(int n, int r){
if(com[n][r] != 0) return com[n][r];
if(r == 0 || n == r) return 1;
else return com[n][r] = Combi(n-1, r-1) + Combi(n-1, r);
}
public void DFS(int L, int sum){
if(flag) return;
if(L == n){
if(sum == f) {
flag = true;
for(int i : p) System.out.print(i + " ");
}
}
else{
for(int i = 1; i <= n; i++){
if(ch[i] == 0){
ch[i] = 1;
p[L] = i;
DFS(L+1, sum+(p[L]*c[L]));
ch[i] = 0;
}
}
}
}
public static void main(String[] args){
Main T = new Main();
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
f = sc.nextInt();
c = new int[n];
p = new int[n];
ch = new int[n+1];
// 각 자리수의 사용횟수 세팅
for(int i = 0; i < n; i++){
c[i] = T.Combi(n-1, i);
}
T.DFS(0, 0);
}
}조합 구하기

🔍풀이
중복되지않는 조합 찾기문제
public void DFS(int L, int i){
if(L == m){
for(int k : arr) System.out.print(k + " ");
System.out.println();
}else{
for(int j = i; j <= n; j++){
arr[L] = j;
DFS(L+1, j+1);
}
}
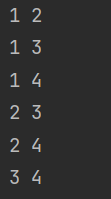
}출력결과
미로 탐색
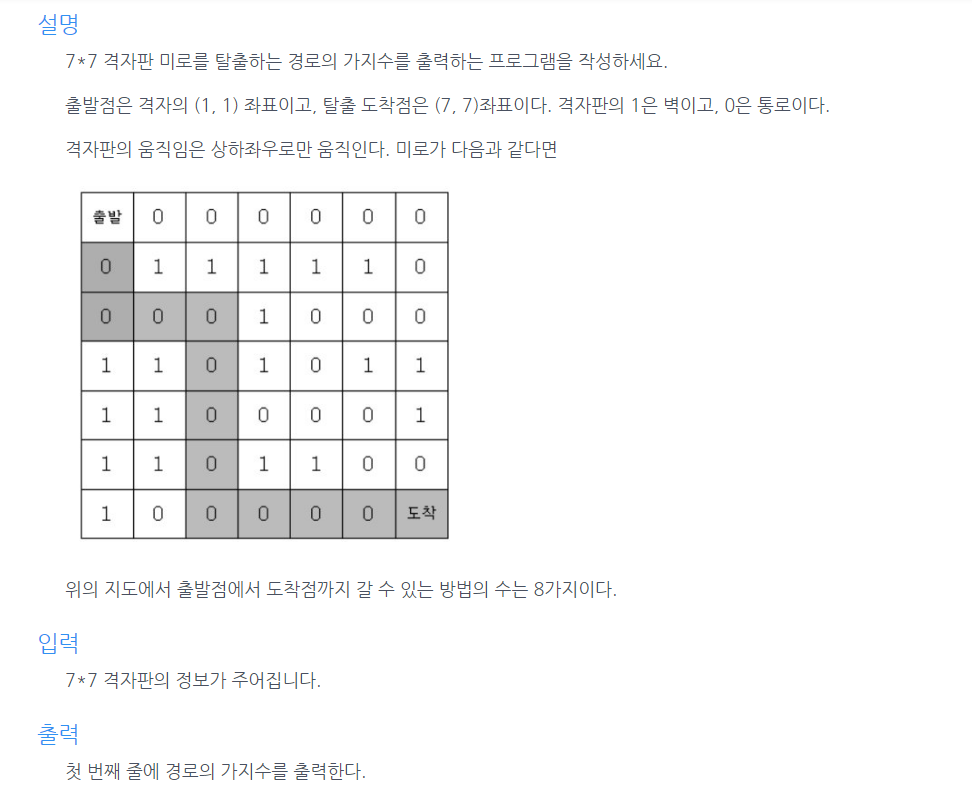
왔던 길은 1로 막고, 0이되는 길은 무조건 찾아가도록 코드 작성
public class Main {
static int[] dx = {-1, 0, 1, 0};
static int[] dy = {0, 1, 0, -1};
static int answer = 0;
static int[][] board = new int[8][8];
public void DFS(int x, int y){
if(x == 7 && y == 7) answer++;
else{
for(int i = 0; i < 4; i++){
int nx = x+dx[i];
int ny = y+dy[i];
if(nx>=1 && nx <= 7 && ny>= 1 && ny <= 7 && board[nx][ny] == 0){
board[nx][ny] = 1;
DFS(nx, ny);
board[nx][ny] = 0;
}
}
}
}
public static void main(String[] args) {
Main T = new Main();
Scanner sc = new Scanner(System.in);
for(int i = 1; i <= 7; i++){
for(int j = 1; j <= 7; j++){
board[i][j] = sc.nextInt();
}
}
board[1][1] = 1;
T.DFS(1, 1);
System.out.println(answer);
}
}섬나라 아일랜드

public class Main {
static int n, answer = 0;
static int[][] board, ch;
int[] dx = {1, -1, 0, 0, -1, 1, -1, 1};
int[] dy = {0, 0, 1, -1, -1, 1, 1, -1};
public void DFS(int x, int y){
for(int i = 0; i < 8; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx >=0 && ny >= 0 && nx < n && ny < n && board[nx][ny] == 1 && ch[nx][ny] == 0) {
// 섬이지만, 안가본 곳은 추가해줌
ch[nx][ny] = 1;
DFS(nx, ny);
}
}
}
public static void main(String[] args) {
Main T = new Main();
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
board = new int[n][n];
ch = new int[n][n];
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
board[i][j] = sc.nextInt();
}
}
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(board[i][j] == 1 && ch[i][j] == 0) {
answer++;
ch[i][j] = 1;
T.DFS(i, j);
}
}
}
System.out.println(answer);
}
}피자배달거리
class Main {
static ArrayList<Point2> house, store;
static int[] combi;
static int answer = Integer.MAX_VALUE;
public void DFS(int i, int m, int L) {
if(L == m) {
int sum = 0;
for(Point2 houses : house) {
int dis = Integer.MAX_VALUE;
for(int k = 0; k < m; k++) {
Point2 stores = store.get(combi[k]);
int x = Math.abs(houses.x - stores.x);
int y = Math.abs(houses.y - stores.y);
dis = Math.min(dis, x+y);
}
sum += dis;
}
answer = Math.min(answer, sum);
}else {
for(int j = i; j < store.size(); j++) {
combi[L] = j;
DFS(j+1, m, L+1);
}
}
//m개만큼 선택해서, 각각 피자배달거리를 다 반복문으로 돌려서 구해야함.
//우선 피자집에서 m개를 선택하는 알고리즘이 필요.
//2.선택해서 각 집마다 거리를 구해서 최소거리로 변경해서 다 더해야함.
//store.size에서 m개를 선택하는 콤비 dfs
}
public static void main(String[] args) {
Main main = new Main();
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
house = new ArrayList<>();
store = new ArrayList<>();
combi = new int[m];
// 좌표만 저장해서 서로 비교
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
int k = sc.nextInt();
if(k == 1) house.add(new Point2(i, j));
else if(k == 2) store.add(new Point2(i, j));
}
}
main.DFS(0, m, 0);
System.out.println(answer);
}
}