스택이란?
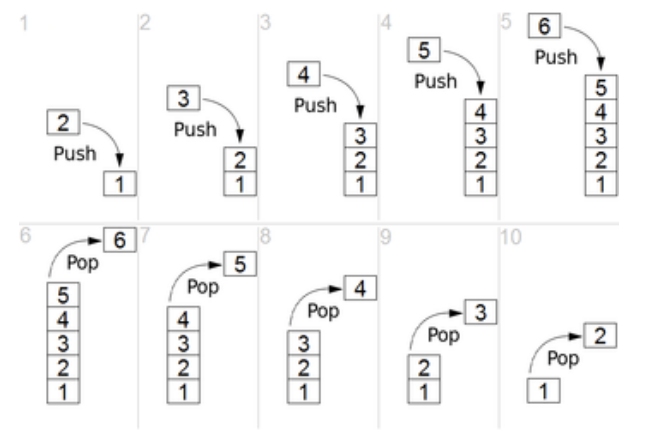
스택(stack) 자료구조는 일상 생활에서 쌓인 접시나 책과 같은 것들을 떠올리면 이해하기 쉽습니다. 스택은 데이터를 순차적으로 저장하고 접근할 수 있는 자료구조로, 핵심 원칙은 가장 마지막에 추가된 데이터가 가장 먼저 제거된다는 것입니다. 이 원칙은 LIFO(Last In, First Out)라고도 불립니다.
스택에서는 주로 두 가지 연산을 수행합니다:
- 푸시(Push): 스택의 맨 위에 데이터를 추가하는 것입니다.
- 팝(Pop): 스택의 맨 위에서 데이터를 제거하고 반환하는 것입니다.
스택은 프로그래밍에서 다양한 문제를 해결하기 위해 사용되며, 예를 들어 함수 호출 스택, 괄호 짝 맞추기, 후위 표기법 계산 등에서 사용됩니다.
- 스택 사용 예
1) 함수 호출 스택:
프로그램에서 함수가 호출되면, 그 함수의 실행을 시작하기 전에 현재 실행 중인 함수의 정보와 다음 실행할 명령어의 주소가 스택에 저장됩니다. 이 정보를 '스택 프레임'이라고 합니다. 이후, 새로 호출된 함수가 실행되고 완료되면, 스택의 가장 위에 있는 스택 프레임이 제거되고, 이전 함수로 돌아갑니다. 이렇게 스택을 사용하면 프로그램의 실행 순서와 함수 호출 관계를 관리할 수 있습니다.예를 들어, 함수 A가 호출되어 실행 중일 때, 함수 B를 호출한다고 가정해봅시다. 이 때, 스택에는 함수 A의 스택 프레임이 저장되고, 그 위에 함수 B의 스택 프레임이 저장됩니다. 함수 B가 실행을 완료하면, 스택에서 함수 B의 스택 프레임이 제거되고, 함수 A로 돌아가서 실행을 이어갑니다.
2)괄호 짝 맞추기:
스택은 괄호 짝 맞추기 문제에서도 유용하게 사용됩니다. 예를 들어, 괄호가 올바르게 짝을 이루고 있는지 확인하는 알고리즘을 작성한다고 가정해봅시다. 이 경우, 스택을 사용하여 다음과 같이 처리할 수 있습니다.- 입력 문자열을 순회하며 각 문자를 확인합니다.
- 여는 괄호('(')를 만나면, 스택에 여는 괄호를 푸시합니다.
- 닫는 괄호(')')를 만나면, 스택에서 팝하여 여는 괄호를 제거합니다. 이때, 스택이 비어있다면 짝이 맞지 않는 것으로 판단할 수 있습니다.
- 모든 문자를 확인한 후, 스택이 비어있다면 괄호가 올바르게 짝을 이룬 것입니다. 스택에 남아있는 괄호가 있다면 짝이 맞지 않는 것으로 판단합니다.
3) 후위 표기법(Postfix Notation)은 연산자를 피연산자 뒤에 위치시키는 수학 표기법으로, 컴퓨터에서 산술 연산을 수행할 때 효율적인 방법입니다. 후위 표기법 계산에서 스택이 어떻게 사용되는지 이해하기 쉽게 설명하겠습니다.
후위 표기법으로 주어진 수식을 계산하는 과정은 다음과 같습니다:
- 입력 문자열을 왼쪽에서 오른쪽으로 순회하면서 각 문자를 확인합니다.
- 피연산자(숫자)를 만나면 스택에 푸시합니다.
- 연산자(+, -, *, / 등)를 만나면 스택에서 팝을 통해 두 개의 피연산자를 꺼냅니다. 이때, 먼저 팝한 값이 오른쪽 피연산자, 나중에 팝한 값이 왼쪽 피연산자가 됩니다.
- 꺼낸 두 피연산자에 대해 해당 연산자를 적용한 결과를 다시 스택에 푸시합니다.
- 입력 문자열의 모든 문자를 확인한 후, 스택에 남아있는 값이 최종 계산 결과입니다.
간단한 예를 들어보겠습니다. 후위 표기법으로 주어진 수식이 "5 3 2 * + 4 -"라고 가정해봅시다. 이 수식을 계산하는 과정은 다음과 같습니다:
- 5를 스택에 푸시합니다. (스택: [5])
- 3을 스택에 푸시합니다. (스택: [5, 3])
- 2를 스택에 푸시합니다. (스택: [5, 3, 2])
- 연산자를 만나면, 스택에서 2와 3을 팝하고, 이 둘을 곱한 결과인 6을 스택에 푸시합니다. (스택: [5, 6])
- 연산자를 만나면, 스택에서 6과 5를 팝하고, 이 둘을 더한 결과인 11을 스택에 푸시합니다. (스택: [11])
- 4를 스택에 푸시합니다. (스택: [11, 4])
- 연산자를 만나면, 스택에서 4와 11을 팝하고, 이 둘을 뺀 결과인 7을 스택에 푸시합니다. (스택: [7])
이제 스택에 남아있는 값은 7이므로, 최종 계산 결과는 7입니다. 이렇게 스택을 사용하여 후위 표기법으로 주어진 수식을 효과적으로 계산할 수 있습니다. 스택을 사용함으로써 연산자 우선순위를 고려할 필요가 없고, 괄호를 사용하지 않아도 됩니다. 이로 인해 후위 표기법은 컴퓨터에서 산술 연산을 수행하는 데 효율적인 방법으로 활용됩니다.
앞서 예시에서처럼, 후위 표기법으로 표현된 수식을 계산할 때 스택을 사용하여 피연산자를 저장하고, 연산자가 나타날 때마다 스택에서 피연산자를 꺼내 계산한 뒤 결과를 다시 스택에 저장하는 과정을 반복합니다. 이 과정을 문자열의 끝까지 진행한 후 스택에 남아있는 값이 최종 계산 결과가 됩니다.
간단한 예시로, 책을 쌓아두는 것을 생각해보세요. 책을 차례대로 쌓으면서, 가장 마지막에 쌓은 책을 가장 먼저 꺼내어 읽습니다. 이것이 바로 스택의 동작 방식입니다.
장점:
- 구현이 간단하고 효율적입니다. 푸시(저장)와 팝(읽기) 연산은 일반적으로 O(1)의 시간 복잡도를 가집니다.
- LIFO 원칙 덕분에 함수 호출, 괄호 검사, 후위 표기법 계산 등에서 자연스럽게 사용됩니다.
- 스택은 메모리 관리에 있어 연속적인 메모리 할당을 최소화하며, 메모리 단편화를 줄일 수 있습니다.
- 스택을 사용하면 명확한 작업 순서를 정의할 수 있습니다. 예를 들어, 컴파일러 및 인터프리터에서 문법을 해석하거나 연산 순서를 관리하는 데 사용됩니다.
단점:
- 스택의 크기는 고정되거나 동적으로 할당되어야 하며, 크기 제한으로 인해 오버플로우(Overflow) 문제가 발생할 수 있습니다.
- 데이터 접근이 제한적입니다. 스택에서는 가장 위에 있는 요소만 확인하거나 제거할 수 있습니다. 이로 인해 중간에 있는 요소에 접근하려면 모든 위쪽 요소를 제거해야 합니다.
- 스택은 탐색이나 정렬과 같은 작업에는 적합하지 않습니다. 이러한 작업을 수행하려면 다른 자료구조(예: 배열, 연결 리스트)를 사용하는 것이 좋습니다.
- 상세 설명
스택은 탐색이나 정렬과 같은 작업에 적합하지 않은 이유는 주로 자료구조의 특성과 접근 방식 때문입니다. 스택은 LIFO(Last In First Out) 원칙에 따라 동작하는 자료구조로, 가장 마지막에 들어온 요소가 가장 먼저 나가게 됩니다. 이 특성 때문에 스택에서 발생하는 문제점들을 살펴보겠습니다.
- 제한된 접근: 스택에서는 가장 위에 있는 요소만 확인하거나 제거할 수 있습니다. 따라서 중간에 있는 요소에 접근하려면 상위 요소들을 모두 제거해야 합니다. 이는 탐색 작업에 있어 매우 비효율적입니다.
- 데이터 이동 비용: 스택에서 중간 요소에 접근하거나, 삽입 및 삭제를 수행하려면 상위 요소들을 제거하고 다시 스택에 넣는 작업이 필요합니다. 이 과정에서 발생하는 데이터 이동 비용이 크기 때문에, 스택은 정렬 작업에 비효율적입니다.
- 구조적 한계: 스택은 선형 구조로, 한쪽 끝에서만 작업을 수행할 수 있습니다. 따라서 탐색이나 정렬 작업을 수행할 때, 요소들 간의 상대적 위치를 변경하거나 한 번에 여러 요소에 접근하는 것이 어렵습니다.
이러한 이유로, 스택은 탐색이나 정렬 작업에 적합하지 않습니다. 이와 같은 작업을 수행할 때는 다른 자료구조를 사용하는 것이 더 효율적입니다. 예를 들어, 배열이나 연결 리스트는 임의의 위치에 있는 요소에 쉽게 접근할 수 있으며, 정렬 알고리즘을 적용하기에 더 적합한 구조를 가지고 있습니다.
- 상세 설명
- 데이터 최대 갯수를 미리 정해야 합니다. (파이썬의 경우 재귀 함수는 1000번까지만 호출이 가능)
- 미리 최대 갯수만큼 저장 공간을 확보해야 하므로 저장 공간의 낭비가 발생할 수 있습니다.
적합한 상황:
- 함수 호출 및 반환 관리: 프로그램 실행 시 함수 호출에 관한 정보를 저장하고 관리하는 데 사용됩니다.
- 괄호 검사: 괄호가 올바르게 열리고 닫히는지 검사하는 데 사용됩니다.
- 후위 표기법 계산: 후위 표기법으로 표현된 수식을 효율적으로 계산하는 데 사용됩니다.
부적합한 상황:
- 데이터 탐색: 스택은 중간에 있는 요소에 쉽게 접근할 수 없기 때문에 탐색 작업에는 부적합합니다.
- 정렬: 스택은 정렬 작업에 적합하지 않습니다. 정렬 작업을 수행하려면 다른 자료구조를 사용하는 것이 더 효율적입니다. 예를 들어, 배열이나 연결 리스트를 사용하면 데이터의 정렬이나 탐색 작업을 쉽게 수행할 수 있습니다.
- 임의의 위치에 있는 요소에 접근, 삽입, 삭제가 필요한 경우: 스택은 가장 위에 있는 요소에만 접근할 수 있기 때문에, 임의의 위치에서 요소를 삽입하거나 삭제하는 작업에는 부적합합니다. 이 경우 연결 리스트, 트리 등의 자료구조가 더 적합할 수 있습니다.
- 공간 효율성이 중요한 경우: 스택은 고정된 크기를 가지거나 동적으로 메모리를 할당하기 때문에, 공간 사용에 있어 비효율적일 수 있습니다. 이러한 상황에서는 공간 효율성이 높은 다른 자료구조를 사용하는 것이 좋습니다.
주의사항:
- 스택 오버플로우: 스택이 가득 차면 더 이상 요소를 추가할 수 없습니다. 이러한 상황에서 요소를 추가하려고 하면 스택 오버플로우가 발생합니다. 스택 크기를 적절하게 설정하거나 동적으로 할당하는 방법으로 이 문제를 해결할 수 있습니다.
- 스택 언더플로우: 스택이 비어 있는 상태에서 요소를 제거하려고 하면 스택 언더플로우가 발생합니다. 이를 방지하기 위해 팝(Pop) 연산을 수행하기 전에 스택이 비어 있는지 확인하는 것이 중요합니다.
- 메모리 관리: 동적으로 할당된 스택의 경우, 메모리 누수를 방지하기 위해 사용이 끝난 후 메모리를 반드시 해제해야 합니다. 또한 스택 크기를 적절하게 관리하여 메모리 사용량을 최적화해야 합니다.
- 스택 사용의 적절성: 스택은 특정한 작업에 적합하지만, 다른 작업에는 부적합할 수 있습니다. 예를 들어, 데이터 탐색이나 정렬 작업에 스택을 사용하는 것은 비효율적입니다. 이 경우 배열이나 연결 리스트와 같은 다른 자료구조를 사용하는 것이 더 효율적입니다.
- 멀티스레드 환경에서의 동기화: 멀티스레드 환경에서 스택을 사용할 때는 동시성 문제를 고려해야 합니다. 여러 스레드가 동시에 스택에 접근하면 데이터의 무결성이 깨질 수 있습니다. 이를 방지하기 위해 동기화 기법을 사용하여 스레드 간의 작업 순서를 제어해야 합니다.
이처럼 스택은 특정 상황에는 매우 유용한 자료구조이지만, 다양한 작업을 수행하는데 있어서는 부적합한 경우도 있습니다. 사용할 작업의 요구사항에 따라 적절한 자료구조를 선택하는 것이 중요합니다.
스택 구현
Pyton
# 재귀 함수
def recursive(data):
if data < 0:
print ("ended")
else:
print(data)
recursive(data - 1)
print("returned", data)
recursive(4)
# 4
# 3
# 2
# 1
# 0
# ended
# returned 0
# returned 1
# returned 2
# returned 3
# returned 4파이썬 리스트 기능에서 제공하는 메서드로 스택 사용해보기
append(push), pop 메서드 제공
data_stack = list()
data_stack.append(1)
data_stack.append(2)
data_stack
# [1, 2]
data_stack.pop()
# 2
data_stack.pop()
# 1리스트 변수로 스택을 다루는 pop, push 기능 구현해보기 (pop, push 함수 사용하지 않고 직접 구현해보기)
stack_list = list()
def push(data):
stack_list.append(data)
def pop():
data = stack_list[-1]
del stack_list[-1]
return data
for index in range(10):
push(index)
pop()
# 9
pop()
# 8
pop()
# 7
pop()
# 6JS
class Stack {
items = [];
// 스택에 새로운 요소를 추가
push(element) {
this.items.push(element);
}
// 스택에서 가장 위에 있는 요소를 제거하고 반환
pop() {
if (this.isEmpty()) {
return "Stack is empty";
}
const lastItem = this.items[this.items.length - 1];
this.items.length -= 1; // 렝스를 줄이면 내부적으로 마지막 요소 삭제됨
return lastItem;
}
// 스택의 가장 위에 있는 요소를 반환
peek() {
if (this.isEmpty()) {
return "Stack is empty";
}
return this.items[this.items.length - 1];
}
// 스택이 비어있는지 확인
isEmpty() {
return this.items.length === 0;
}
// 스택의 길이를 반환
size() {
return this.items.length;
}
// 스택의 모든 요소를 제거
clear() {
this.items = [];
}
// 스택의 요소를 문자열로 반환
toString() {
return this.items.toString();
}
}
// 사용 예시
const stack = new Stack();
stack.push(1);
stack.push(2);
stack.push(3);
console.log(stack.peek()); // 출력: 3
console.log(stack.pop()); // 출력: 3
console.log(stack.size()); // 출력: 2